A quantity of air is kept in a container having walls which are slightly conducting. The initial temperature and volume are 270C (equal to the temperature of the surrounding) and 800cm3 respectively. Find the rise in the temperature if the gas is compressed to 200cm3 (a) in a short time (b) in a long time . Take gamma= 1.4.
To solve the problem step by step, we will analyze both parts of the question regarding the compression of air in the container.
Given Data:
- Initial Temperature, T1=27∘C=300K (converted to Kelvin)
- Initial Volume, V1=800cm3
- Final Volume, V2=200cm3
- γ=1.4
Part (a): Compression in a Short Time (Adiabatic Process)
1. Understand the Adiabatic Process:
In an adiabatic process, there is no heat exchange with the surroundings. The relationship between temperature and volume is given by:
T1⋅Vγ−11=T2⋅Vγ−12
2. Rearranging the Equation:
We can rearrange this equation to find T2:
T2=T1⋅(V1V2)γ−1
3. Substituting the Values:
- T1=300K
- V1=800cm3
- V2=200cm3
- γ−1=1.4−1=0.4
Now substitute these values into the equation:
T2=300⋅(800200)0.4
4. Calculating the Volume Ratio:
800200=4
5. Calculating T2:
T2=300⋅40.4
Now calculate 40.4:
40.4≈2.297
Therefore,
T2≈300⋅2.297≈689.1K
6. Finding the Change in Temperature:
ΔT=T2−T1=689.1−300=389.1K
Part (b): Compression in a Long Time (Isothermal Process)
1. Understand the Isothermal Process:
In an isothermal process, the temperature remains constant because there is sufficient time for heat transfer. Thus, the final temperature T2 will be equal to the initial temperature T1.
2. Conclusion for Isothermal Process:
ΔT=T2−T1=0K
Final Answers:
- (a) The rise in temperature when compressed quickly (adiabatically) is approximately 389.1K.
- (b) The rise in temperature when compressed slowly (isothermally) is 0K.
- Initial Temperature, T1=27∘C=300K (converted to Kelvin)
- Initial Volume, V1=800cm3
- Final Volume, V2=200cm3
- γ=1.4
In an adiabatic process, there is no heat exchange with the surroundings. The relationship between temperature and volume is given by:
T1⋅Vγ−11=T2⋅Vγ−12
We can rearrange this equation to find T2:
T2=T1⋅(V1V2)γ−1
- T1=300K
- V1=800cm3
- V2=200cm3
- γ−1=1.4−1=0.4
T2=300⋅(800200)0.4
800200=4
T2=300⋅40.4
Now calculate 40.4:
40.4≈2.297
Therefore,
T2≈300⋅2.297≈689.1K
ΔT=T2−T1=689.1−300=389.1K
In an isothermal process, the temperature remains constant because there is sufficient time for heat transfer. Thus, the final temperature T2 will be equal to the initial temperature T1.
ΔT=T2−T1=0K
- (a) The rise in temperature when compressed quickly (adiabatically) is approximately 389.1K.
- (b) The rise in temperature when compressed slowly (isothermally) is 0K.
Topper's Solved these Questions
Similar Questions
A container having slightly conducting walls contains air. The initial temperature and volume are 47∘C (equal to the temperature of the surrounding) and 400cm3 respectively. Find the rise in the temperature if the gas is compressed to 200cm3 (a) in a short time (b) in a short time (b) in a along time. Take γ=1.4.[20.4=1.3]
View SolutionIn fig. the walls of the container and the piston are weakly conducting. The initial pressure, volume and temperature of the gas are 200KPa,800cm3 and 100Kresp. Find the pressure and the temperature of the gas it it is (a) slowly compressed (b) suddenly compressed to 200cm3(γ=1.5).
 View Solution
View SolutionA gas is enclosed in a cylindrical can fitted with a piston. The walls of the can and the piston are adiabatic. The initial pressure , volume and temperature of the gas are 100kPa,400cm3 and 300K respectively. The ratio of the specific heat capacities of the gas is (CpCv=1.5) Find the pressure and the temperature of the gas if it is (a) suddenly compressed (b) slowly compressed to 100cm3.
View SolutionIn a steady state of thermal conduction, temperature of the ends A and B of a 20 cm long rod are 100∘C and 0∘C respectively. What will be the temperature of the rod at a point at a distance of 9 cm from the end A of the rod
View SolutionA monatomic ideal gas is contained in a rigid container of volume V with walls of total inner surface area A, thickness x and thermal conductivity K. The gas is at an initial temperature t0 and pressure P0 . Find the pressure of the gas as a function of time if the temperature of the surrounding air is Ts . All temperature are in absolute scale.
View SolutionOne mode of an ideal monatomic gas is kept in a rigid vessel. The vessel is kept inside a steam chamber whose temperature is 97∘C . Initially, the temperature of the gas is 5.0∘C . The walls of the vessel have an inner surface of area 800cm2 and thickness 1.0cm If the temperature of the gas increases to 9.0∘C in 5.0 second, find the thermal conductivity of the material of the walls.
View SolutionA cyclinder with a movable piston contains 3mols of hydrogen at standard temperature and pressure. The walls of the cyclinder are made of a heat insulator, and the piston is insulated by having a pile of sand on it. By what factor does the pressure of the gas increases, if the gas is compressed to half its original volume? Given γ=1.4.
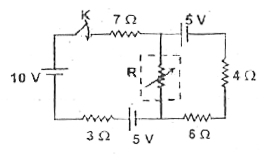
View SolutionIn the circuit shown the resistance R is kept in a chamber whose temperature. is 20∘C which remains constant. The initial temperature and resistance of R is 50∘C and 15Ωrespectively. The rate of change of resistance R with temperature is 12Ω/∘C and the rate of decrease of temperature of R is In(3/100) times the temperature difference from the surrounding (Assume the resistance R loses heat only in accordance with Newton's law of cooling) If K is closed at t = 0, then find the
(a) value of. R for which power dissipation in it is maximum.
(b) temperature of R when power dissipation is maximum
(c) time after which the power dissipation will be maximum
 View Solution
View SolutionAir contained in a cylinder at 20.0∘C is compressed froma n initial pressure of 1.00 atm, and volume of 700cm3 to a volume of 70.0cm3 . If the final pressure is 15.0 atm then what is the final temperature?
View SolutionA certain quantity of air is adiabatically compressed so that its pressure increases from 1 atmosphere to 150 atmosphere. If the initial temperature of air is 27∘C. Calculate (i) rise in temperature and (ii) the work done of air Y= 1.4).
View Solution

