Figure shown two adiabatic vessels, each containing a mass m of water at different temperature. The ends of a metal rod of length L, area of cross section A and thermal conductivity K, are inserted in the water as shown in the figure. Find the time taken for the difference between the temperature in the vessels to become half of the original value. The specific heat capacity of water is s. Neglect the heat capacity of the rod and the container and any loss of heat to the atmosphere.

The correct Answer is:A, B
(Qt)=KA(T1−T2)Lms
Rise∈temperature∈T2=KA(T1−T2)Lms
Fall in temperature om
T1=KA(T1−T2)Lms
F∈altempertureT1=T1−KA(T1−T2)Lms
F∈altemperatureT2=T2+KA(T1−T2)Lms
⇒dTdt=2KA(T1−T2)Lms
⇒InT1−T22(T1−T2)=2KALmst
In2=2KALmst
t=Lms2KAIn2.

Topper's Solved these Questions
- HEAT TRANSFERBOOK - HC VERMA ENGLISHCHAPTER - HEAT TRANSFEREXERCISE - QUESTIONS FOR SHORT ANSWER
11 Videos
- HEAT TRANSFERBOOK - HC VERMA ENGLISHCHAPTER - HEAT TRANSFEREXERCISE - OBJECTIVE II
6 Videos
- HEAT AND TEMPERATUREBOOK - HC VERMA ENGLISHCHAPTER - HEAT AND TEMPERATUREEXERCISE - Objective 2
6 Videos
- INTRODUCTION TO PHYSICSBOOK - HC VERMA ENGLISHCHAPTER - INTRODUCTION TO PHYSICSEXERCISE - Question for short Answer
4 Videos
Similar Questions
Figure shows a large tank of water at a constant temperature θ0 and a small vessel containing a mass m of water at an initial temperature θ1(<θ0). A metal rod of length L, area of cross section A and thermal conductivity K connects the two vessels. Find the time taken for the temperature of the water in the smaller vessel to become θ2(θ1<θ2<θ0) . Specific heat capacity of water is s and all other heat capacities are negligible.

View Solution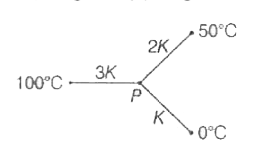
Three rods of the same dimension have thermal conductivity 3K , 2K and K. They are arranged as shown in the figure below
Then , the temperature of the junction in steady - state is
View Solution
Knowledge Check
Two bars of same length and same cross-sectional area but of different thermal conductivites K1 and K2 are joined end to end as shown in the figure. One end of the compound bar it is at temperature T1 and the opposite end at temperature T2 (whereT1>T2). The temperature of the junction is
 AK1T1+K2T2K1+K2BK1T2+K2T1K1+K2CK1(T1+T2)K1+K2DK2T1+T2K1
AK1T1+K2T2K1+K2BK1T2+K2T1K1+K2CK1(T1+T2)K1+K2DK2T1+T2K1
Calculate the difference in temperature between the water at the top and bottom of a water fall 200 m high. Specific heat capacity of water 42000Jkg−1K−1.
View SolutionThree rods of equal length, area of cross section and thermal conductivity are connected as shown in the figure.

There is no heat loss through lateral surface of the rods and temperature of ends are TA=100∘C,TB=70∘C and TC=50∘C. Find the temperature of junction.
View Solution40 g of water at 60∘C is poured into a vessel containing 50 g of water at 20°C. The final temperature of mixture is 30°C. Taking the specific heat capacity of water as 4.2 J g-K-1, calculate the heat capacity of the vessel.
View SolutionThe ends of a copper rod of length 1m and area of cross-section 1cm2 are maintained at 0∘C and 100∘C. At the centre of the rod there is a source of heat of power 25 W. Calculate the temperature gradient in the two halves of the rod in steady state. Thermal conductivity of copper is 400Wm−1K−1.
View SolutionThe ends of a copper rod of length 1m and area of cross-section 1cm2 are maintained at 0∘C and 100∘C. At the centre of the rod there is a source of heat of power 25 W. Calculate the temperature gradient in the two halves of the rod in steady state. Thermal conductivity of copper is 400Wm−1K−1.
View SolutionA rod is heated at one end as shown in figure. In steady state temperature of different sections becomes constant but not same. Why so?
 .
.
View SolutionThe area of cross section of the wider tube shown in figure is 900cm2. If the boy standing on the piston weights 45 kg, find the difference in the levels of water in the two tubes.

View Solution