An amount n (in moles) of a monatomic gas at initial temperature T0 is enclosed in a cylindrical vessel fitted with a light piston. The surrounding air has a temperature Ts(>T0) . And the atmospheric pressure is Pa . Heat may be conducted between the surrounding and the gas through the bottom of the cylinder. The bottom has a surface area A, thickness x and thermal conductivity K. Assuming all change to be slow, find the distance moved by the piston in time t.
The correct Answer is:A, B
To solve the problem step by step, we will analyze the heat transfer and the behavior of the gas in the cylindrical vessel with a piston.
Step 1: Understand the System
We have a monatomic gas in a cylinder with:
- Initial temperature T0
- Surrounding temperature Ts (where Ts>T0)
- Atmospheric pressure Pa
- Surface area A
- Thickness x
- Thermal conductivity K
- Amount of gas n (in moles)
Step 2: Heat Transfer Calculation
The rate of heat transfer dqdt through the bottom of the cylinder can be calculated using Fourier's law of heat conduction:
dqdt=−KA(Ts−T0)x
This equation indicates that heat flows from the surrounding air into the gas.
Step 3: Relate Heat Transfer to Temperature Change
The heat absorbed by the gas can be expressed as:
dq=nCpdT
For a monatomic gas, the specific heat at constant pressure Cp is given by:
Cp=52R
Thus, we can write:
dq=n(52R)dT
Step 4: Set Up the Differential Equation
From the heat transfer and heat absorbed, we can equate:
n(52R)dT=−KA(Ts−T0)xdt
Rearranging gives:
dTTs−T0=−2KA5nRxdt
Step 5: Integrate the Equation
Integrate both sides:
∫TT0dTTs−T0=−2KA5nRx∫t0dt
This leads to:
ln(Ts−TTs−T0)=−2KAt5nRx
Step 6: Solve for Temperature
Exponentiating both sides, we have:
Ts−TTs−T0=e−2KAt5nRx
Rearranging gives:
T=Ts−(Ts−T0)e−2KAt5nRx
Step 7: Relate Temperature Change to Piston Displacement
Using the ideal gas law PV=nRT, we differentiate to find the relationship between the change in volume and temperature:
PdV=nRdT
The change in volume dV can be expressed as:
dV=Adx
Thus:
PAdx=nRdT
From this, we can express dT:
dT=PAdxnR
Step 8: Substitute dT into the Temperature Equation
Substituting dT into our earlier equation gives:
PAdxnR=(Ts−T0)e−2KAt5nRx
Rearranging this, we find:
dx=nRPA(Ts−T0)(1−e−2KAt5nRx)
Step 9: Final Expression for Piston Displacement
Integrating this expression over time will yield the total displacement x of the piston.
Final Result
The distance moved by the piston in time t is given by:
x=nRPaA(Ts−T0)(1−e−2KAt5nRx)
We have a monatomic gas in a cylinder with:
- Initial temperature T0
- Surrounding temperature Ts (where Ts>T0)
- Atmospheric pressure Pa
- Surface area A
- Thickness x
- Thermal conductivity K
- Amount of gas n (in moles)
The rate of heat transfer dqdt through the bottom of the cylinder can be calculated using Fourier's law of heat conduction:
dqdt=−KA(Ts−T0)x
This equation indicates that heat flows from the surrounding air into the gas.
The heat absorbed by the gas can be expressed as:
dq=nCpdT
For a monatomic gas, the specific heat at constant pressure Cp is given by:
Cp=52R
Thus, we can write:
dq=n(52R)dT
From the heat transfer and heat absorbed, we can equate:
n(52R)dT=−KA(Ts−T0)xdt
Rearranging gives:
dTTs−T0=−2KA5nRxdt
Integrate both sides:
∫TT0dTTs−T0=−2KA5nRx∫t0dt
This leads to:
ln(Ts−TTs−T0)=−2KAt5nRx
Exponentiating both sides, we have:
Ts−TTs−T0=e−2KAt5nRx
Rearranging gives:
T=Ts−(Ts−T0)e−2KAt5nRx
Using the ideal gas law PV=nRT, we differentiate to find the relationship between the change in volume and temperature:
PdV=nRdT
The change in volume dV can be expressed as:
dV=Adx
Thus:
PAdx=nRdT
From this, we can express dT:
dT=PAdxnR
Substituting dT into our earlier equation gives:
PAdxnR=(Ts−T0)e−2KAt5nRx
Rearranging this, we find:
dx=nRPA(Ts−T0)(1−e−2KAt5nRx)
Integrating this expression over time will yield the total displacement x of the piston.
The distance moved by the piston in time t is given by:
x=nRPaA(Ts−T0)(1−e−2KAt5nRx)
Topper's Solved these Questions
- BOOK - HC VERMA ENGLISHCHAPTER - HEAT TRANSFEREXERCISE - QUESTIONS FOR SHORT ANSWER11videos
HEAT TRANSFER
- BOOK - HC VERMA ENGLISHCHAPTER - HEAT TRANSFEREXERCISE - OBJECTIVE II6videos
HEAT TRANSFER
- BOOK - HC VERMA ENGLISHCHAPTER - HEAT AND TEMPERATUREEXERCISE - Objective 26videos
HEAT AND TEMPERATURE
- BOOK - HC VERMA ENGLISHCHAPTER - INTRODUCTION TO PHYSICSEXERCISE - Question for short Answer4videos
INTRODUCTION TO PHYSICS
Similar Questions
The air tight and smooth piston of a cylindrical vessel are connected with a string as shown. Initially pressure and temperature of the gas are P0 and T0. The atmospheric pressure is also P0. At a later time, tension in the string is 38P0A where A is the cross-sectional are of the cylinder. at this time, the temperature of the gas has become.
 View Solution
View SolutionA monoatomic ideal gas, initially at temperature T1, is enclosed in a cylinder fitted with a friction less piston. The gas is allowed to expand adiabatically to a temperature T2 by releasing the piston suddenly. If L1andL2 are the length of the gas column before expansion respectively, then T1T2 is given by
View Solution
Knowledge Check
- Question 1 - Select One
A monatomic ideal gas, initially at temperature T1 is enclosed in a cylinder fitted with a frictionless pistion. The gas is allowed to expand adiabatically to a temperature T2. By releasing the piston suddenly. IF L1 and L2 are th lengths of the gas column before and after expansion respectively, then T1/T2 is given by
A(L1/L2)2/3B(L1/L2)C(L2/L1)D(L2/L1) - Question 2 - Select One
A vessel contains 1 mole of O2 gas (relative molar mass 32) at a temperature T. The pressure of the gas is P. An identical vessel containing one mole of He gas (relative molar mass 4) at temperature 2T has a pressure of
AP8BPC2PD8P
A monoatomic ideal gas, initially at temperature T1, is enclosed in a cylinder fitted with a friction less piston. The gas is allowed to expand adiabatically to a temperature T2 by releasing the piston suddenly. If L1andL2 are the length of the gas column before expansion respectively, then T1T2 is given by
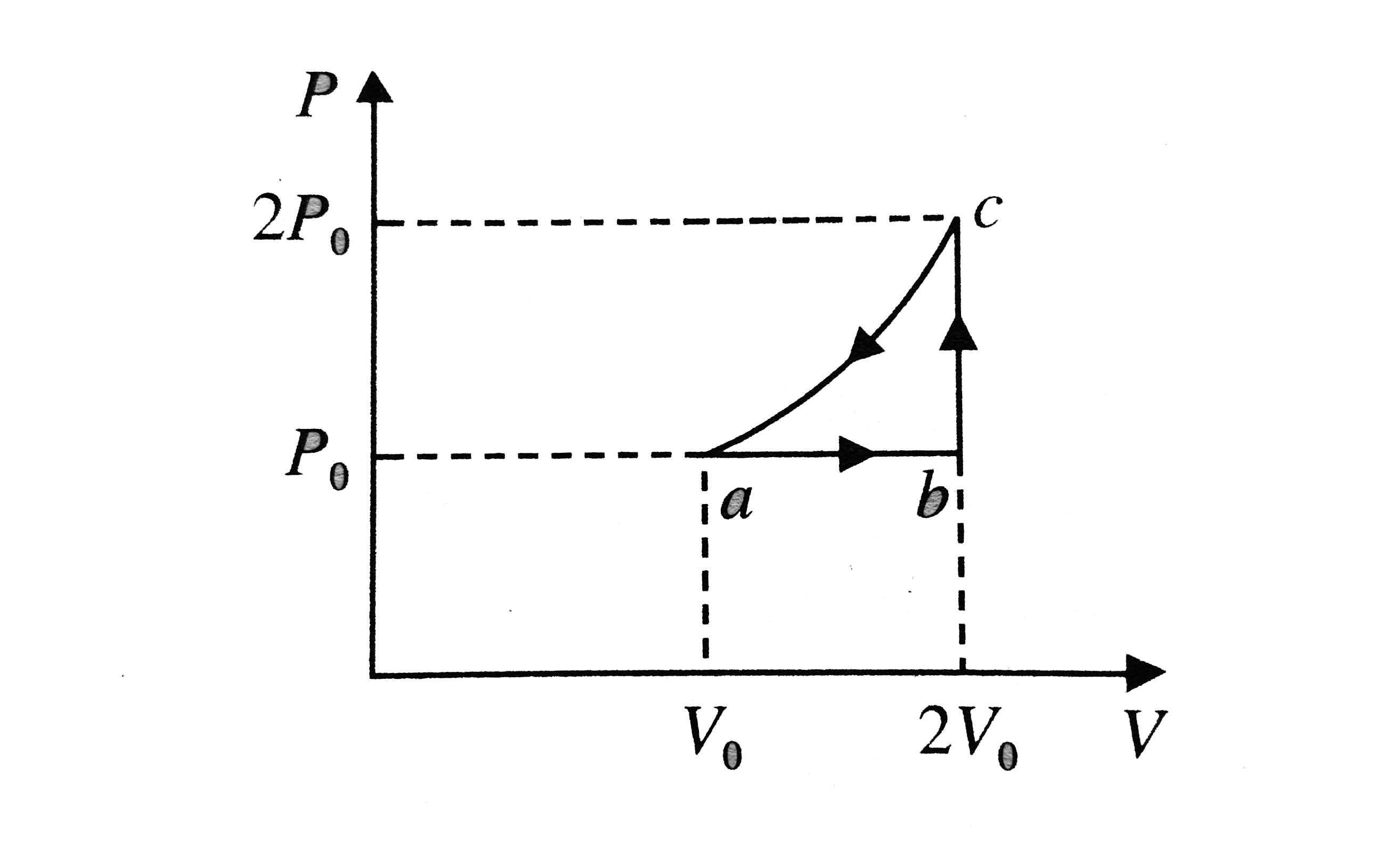
View SolutionOne mole of an ideal monatomic gas has initial temperature T0, is made to go through the cycle abca shown in Fig. If U denotes the internal energy, then choose the correct alternative
 View Solution
View SolutionOne mole of an ideal monatomic gas at temperature T0 expands slowly according to the law P=kV (k is constant). If the final temperature is 4T0 then heat supplied to gas is
View SolutionA gas is enclosed in a cylindrical vessel fitted with a frictionless piston.the gas is slowly heated for some time. During the process, 10 J of heat is supplied and the piston is found to move out 10cm. Find the increase in the internal energy of the gas, the area of cross section of the cylinder=4cm2 and the atmospheric pressure =100kPa.
View SolutionA vessel contains 1 mole of O2 gas (molar mass 32) at a temperature T. The pressure of the gas is P . An identical vessel containing one mole of He gas (molar mass 4) at a temperature 2T has a pressure of xP. Find the value of x.
View SolutionA vessel contains 1 mole of O2 gas (relative molar mass 32) at a temperature T. The pressure of the gas is P. An identical vessel containing one mole of He gas (relative molar mass 4) at temperature 2T has a pressure of
View Solution

