Two equal positive charges are kept at points A and B. The electric potential at the points between A and B (excluding these points ) is studied while moving from A to B. The potential will
To solve the problem of electric potential between two equal positive charges located at points A and B, we can follow these steps:
1. Identify the Charges and Their Positions:
Let the two equal positive charges be Q located at points A and B, separated by a distance D.
2. Choose a Point Between A and B:
Consider a point P located between A and B. Let the distance from charge Q at point A to point P be X. Consequently, the distance from charge Q at point B to point P will be D−X.
3. Calculate the Electric Potential at Point P:
The electric potential V at point P due to both charges can be expressed as:
VP=KQX+KQD−X
where K is Coulomb's constant.
4. Differentiate the Electric Potential:
To understand how the potential changes as we move from A to B, we need to differentiate VP with respect to X:
dVPdX=KQ(−1X2)+KQ(−1(D−X)2)⋅(−1)
Simplifying this gives:
dVPdX=KQ(1(D−X)2−1X2)
5. Analyze the Sign of the Derivative:
- For X<D2: The term 1(D−X)2 is greater than 1X2, hence dVPdX<0. This indicates that the potential decreases as we move from A towards the midpoint.
- For X>D2: The term 1(D−X)2 becomes less than 1X2, hence dVPdX>0. This indicates that the potential increases as we move from the midpoint towards B.
6. Conclusion:
Therefore, as we move from point A to point B, the electric potential first decreases until we reach the midpoint (at X=D2), and then it increases as we continue to point B.
Final Answer:
The electric potential will first decrease and then increase as we move from A to B.
Let the two equal positive charges be Q located at points A and B, separated by a distance D.
Consider a point P located between A and B. Let the distance from charge Q at point A to point P be X. Consequently, the distance from charge Q at point B to point P will be D−X.
The electric potential V at point P due to both charges can be expressed as:
VP=KQX+KQD−X
where K is Coulomb's constant.
To understand how the potential changes as we move from A to B, we need to differentiate VP with respect to X:
dVPdX=KQ(−1X2)+KQ(−1(D−X)2)⋅(−1)
Simplifying this gives:
dVPdX=KQ(1(D−X)2−1X2)
- For X<D2: The term 1(D−X)2 is greater than 1X2, hence dVPdX<0. This indicates that the potential decreases as we move from A towards the midpoint.
- For X>D2: The term 1(D−X)2 becomes less than 1X2, hence dVPdX>0. This indicates that the potential increases as we move from the midpoint towards B.
Therefore, as we move from point A to point B, the electric potential first decreases until we reach the midpoint (at X=D2), and then it increases as we continue to point B.
The electric potential will first decrease and then increase as we move from A to B.
Topper's Solved these Questions
- ELECTRIC FIELD AND POTENTIALBOOK - HC VERMA ENGLISHCHAPTER - ELECTRIC FIELD AND POTENTIALEXERCISE - Objective 2
7 Videos
- ELECTRIC FIELD AND POTENTIALBOOK - HC VERMA ENGLISHCHAPTER - ELECTRIC FIELD AND POTENTIALEXERCISE - question for short answer
14 Videos
- ELECTRIC CURRENT THROUGH GASESBOOK - HC VERMA ENGLISHCHAPTER - ELECTRIC CURRENT THROUGH GASESEXERCISE - Short answer
6 Videos
- ELECTROMAGNETIC INDUCTIONBOOK - HC VERMA ENGLISHCHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - Questions for short answer
9 Videos
Similar Questions
Knowledge Check
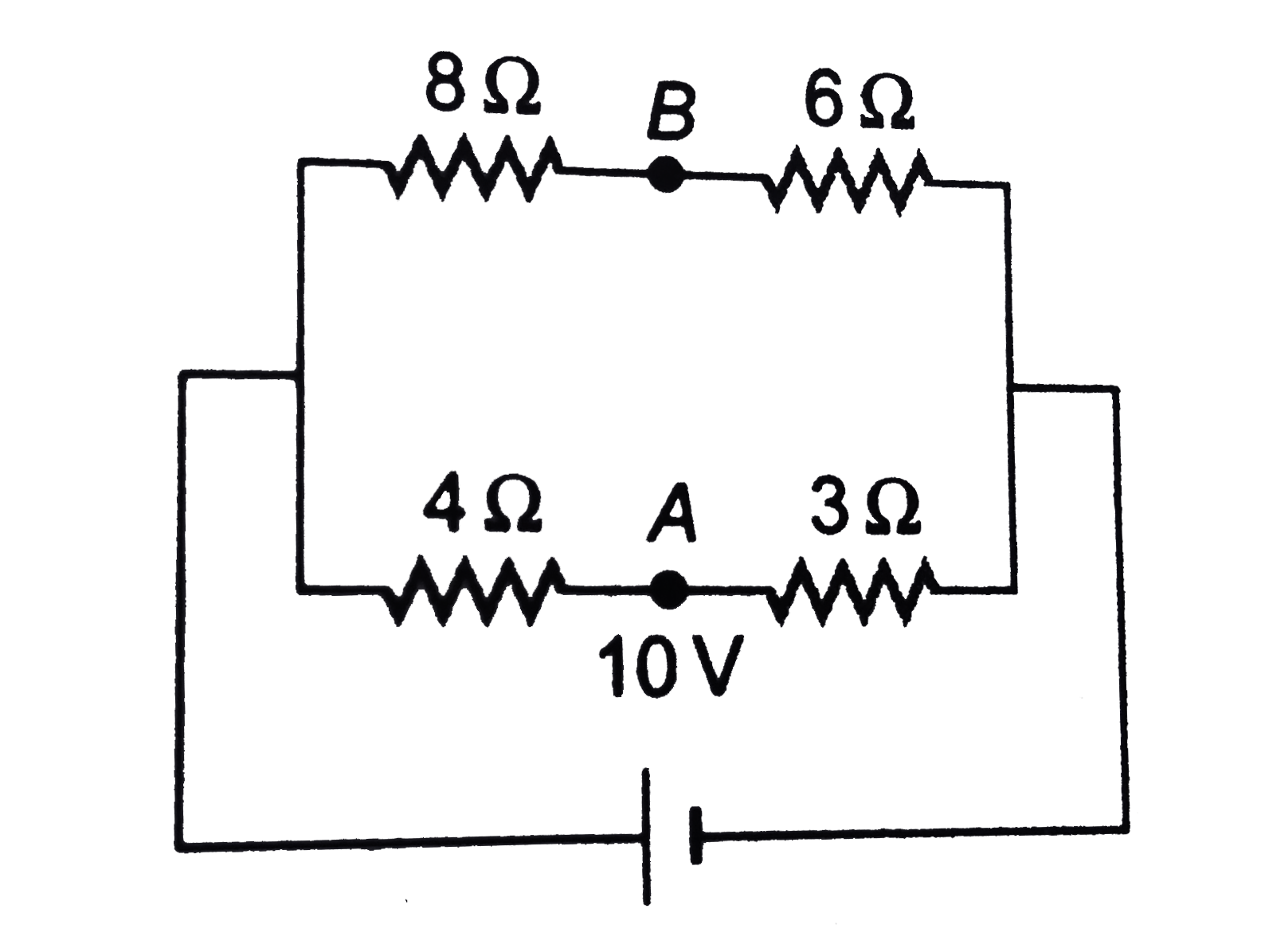
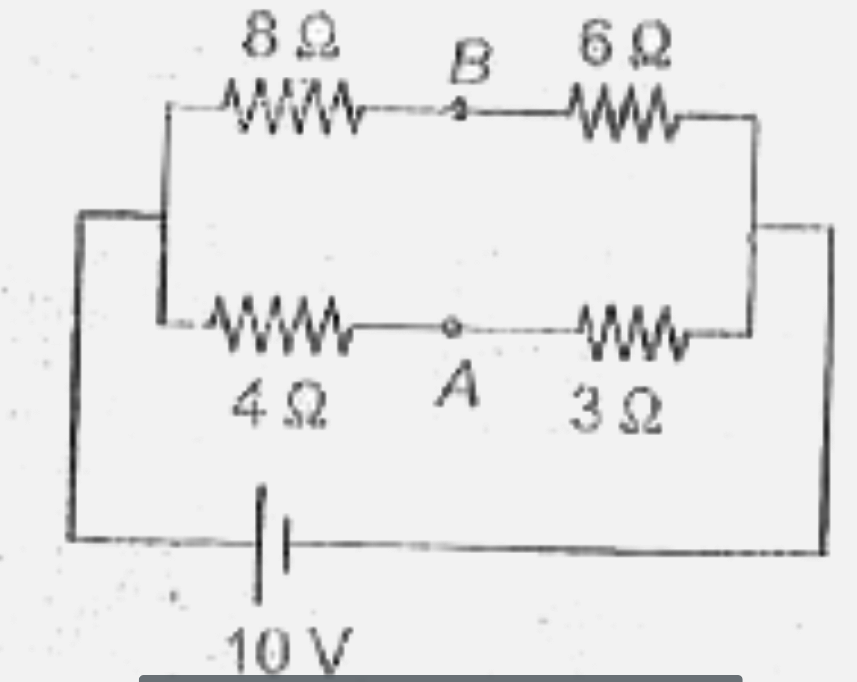
In the given circuit the potential at point B is zero, the potential at points A and D will be
 AVA=4V,VD=9VBVA=3V,VD=4VCVA=9V,VD=3VDVA=4V,VD=3V
AVA=4V,VD=9VBVA=3V,VD=4VCVA=9V,VD=3VDVA=4V,VD=3V
The potential difference between points A and B is
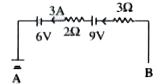
View SolutionThe potential difference between the points A and B in the given circuit is
View SolutionA,B and C are three points in a unifrom electric field. The electric potential is

View SolutionIn the circuit shown, the point B is earthed. The potential at the point 'A' is
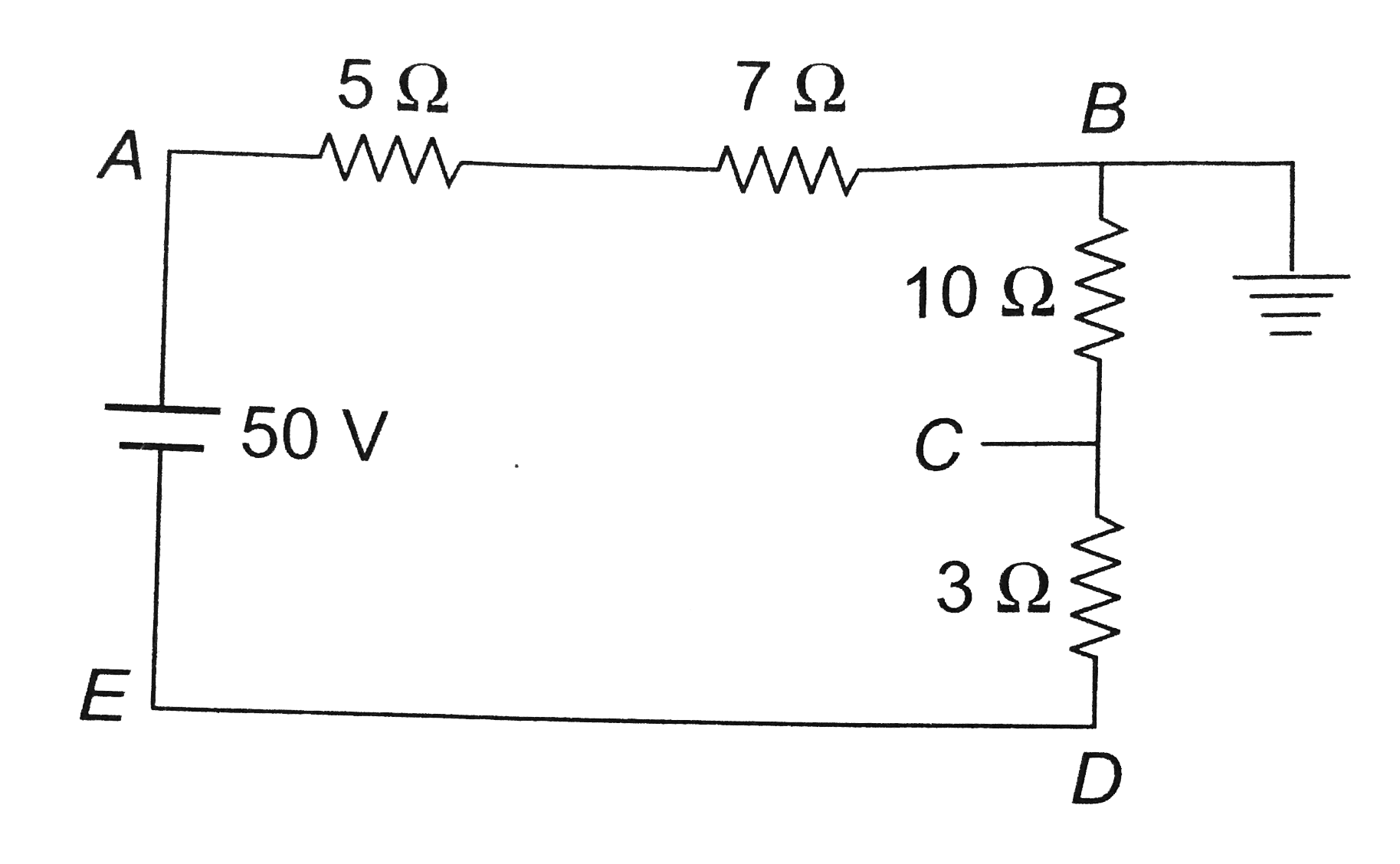
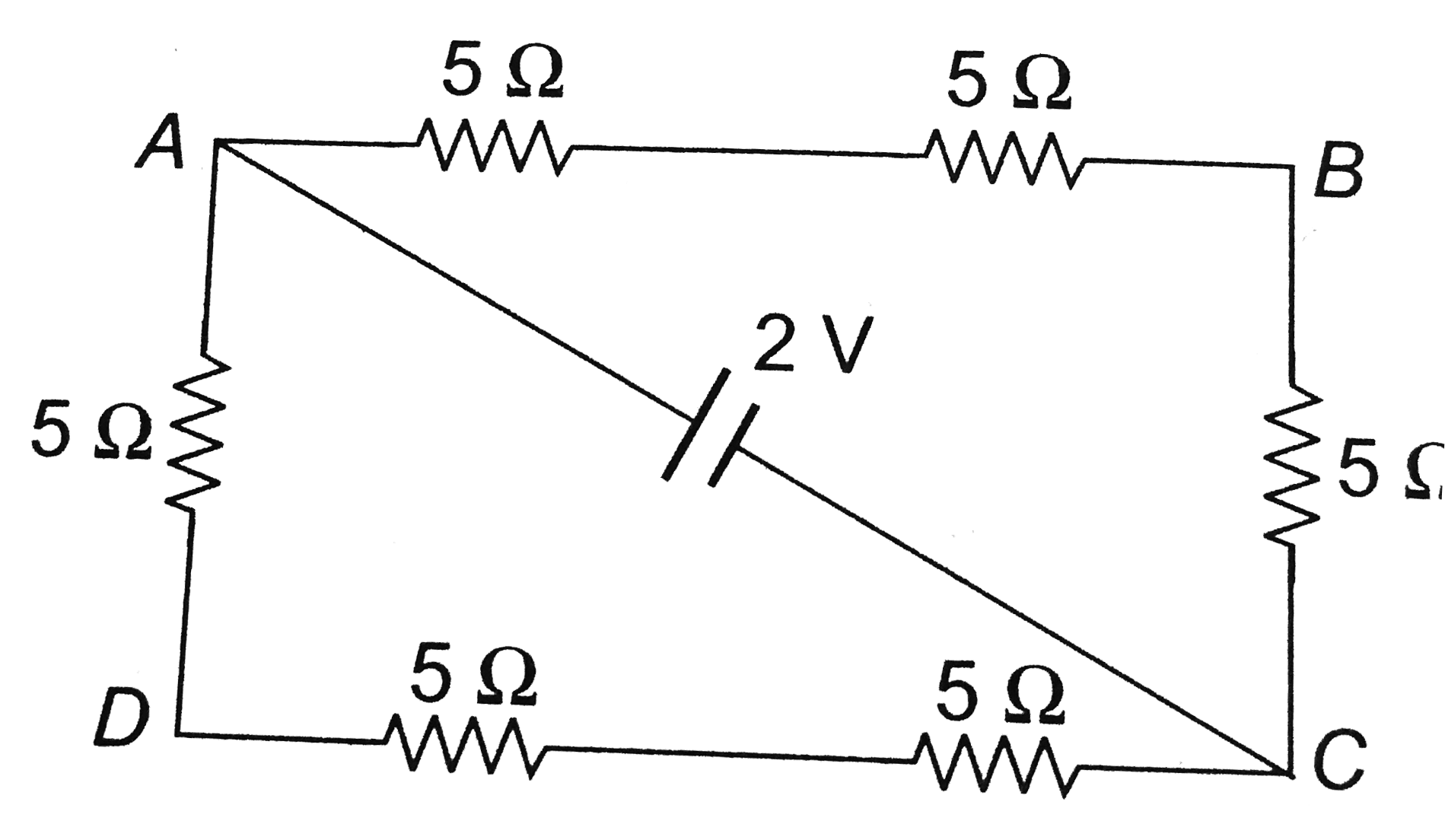
View SolutionThe potential difference between points A and B adjoining figure is
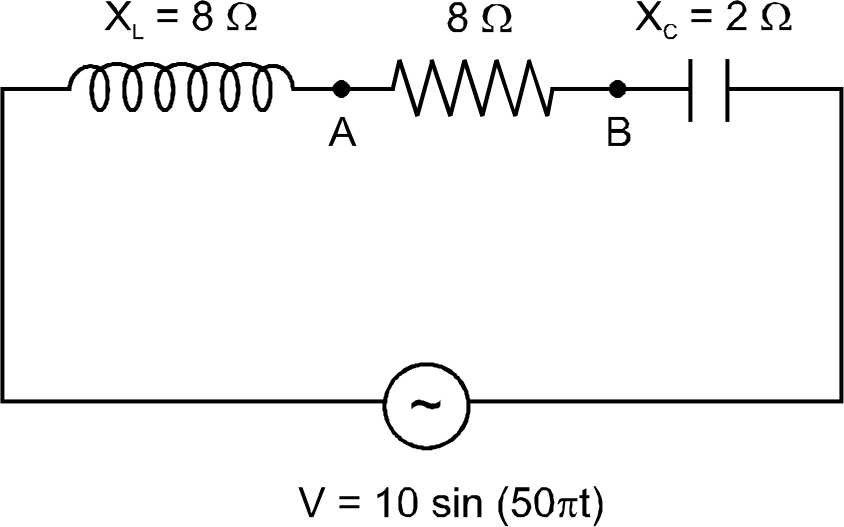
View SolutionThe instantaneous potential differece between points A and B is :
View SolutionWhen a positive q charge is taken from lower potential to a higher potential point, then its potential energy will
View Solution