The electric field at the origin is alo,n,g the positive x-axis. A small circle is drawn with the centre at the origin cutting the axes at points A, B, C and D having coordinates (a,0), (0,a), (-a,0),(0,-a) respectively. Out of the points on the periphery of the circle, the potential is minimum at
A
B
C
D
To solve the problem step-by-step, we will analyze the electric potential at points A, B, C, and D on the periphery of the circle centered at the origin, given that the electric field at the origin is along the positive x-axis.
Step 1: Understanding the Electric Field
The electric field at the origin is given as E=E0^i, which means it points along the positive x-axis.
Step 2: Identifying the Points
The points on the periphery of the circle are:
- Point A: (a,0)
- Point B: (0,a)
- Point C: (−a,0)
- Point D: (0,−a)
Step 3: Formula for Electric Potential
The electric potential V at a point can be calculated using the formula:
V=−E⋅dr
where dr is the displacement vector from the reference point (origin) to the point of interest.
Step 4: Calculating Potential at Each Point
1. Potential at Point A (VA):
- Displacement vector dr=a^i
- Calculation:
VA=−E⋅dr=−E0^i⋅(a^i)=−E0a
2. Potential at Point B (VB):
- Displacement vector dr=a^j
- Calculation:
VB=−E⋅dr=−E0^i⋅(a^j)=0
3. Potential at Point C (VC):
- Displacement vector dr=−a^i
- Calculation:
VC=−E⋅dr=−E0^i⋅(−a^i)=E0a
4. Potential at Point D (VD):
- Displacement vector dr=−a^j
- Calculation:
VD=−E⋅dr=−E0^i⋅(−a^j)=0
Step 5: Summary of Potentials
- VA=−E0a
- VB=0
- VC=E0a
- VD=0
Step 6: Identifying the Minimum Potential
From the calculated potentials:
- VA<VB=VD<VC
Thus, the potential is minimum at point A.
Final Answer
The potential is minimum at point A, which has coordinates (a,0).
---
The electric field at the origin is given as E=E0^i, which means it points along the positive x-axis.
The points on the periphery of the circle are:
- Point A: (a,0)
- Point B: (0,a)
- Point C: (−a,0)
- Point D: (0,−a)
The electric potential V at a point can be calculated using the formula:
V=−E⋅dr
where dr is the displacement vector from the reference point (origin) to the point of interest.
- Displacement vector dr=a^i
- Calculation:
VA=−E⋅dr=−E0^i⋅(a^i)=−E0a
- Displacement vector dr=a^j
- Calculation:
VB=−E⋅dr=−E0^i⋅(a^j)=0
- Displacement vector dr=−a^i
- Calculation:
VC=−E⋅dr=−E0^i⋅(−a^i)=E0a
- Displacement vector dr=−a^j
- Calculation:
VD=−E⋅dr=−E0^i⋅(−a^j)=0
- VA=−E0a
- VB=0
- VC=E0a
- VD=0
From the calculated potentials:
- VA<VB=VD<VC
The potential is minimum at point A, which has coordinates (a,0).
Topper's Solved these Questions
- ELECTRIC FIELD AND POTENTIALBOOK - HC VERMA ENGLISHCHAPTER - ELECTRIC FIELD AND POTENTIALEXERCISE - Objective 2
7 Videos
- ELECTRIC FIELD AND POTENTIALBOOK - HC VERMA ENGLISHCHAPTER - ELECTRIC FIELD AND POTENTIALEXERCISE - question for short answer
14 Videos
- ELECTRIC CURRENT THROUGH GASESBOOK - HC VERMA ENGLISHCHAPTER - ELECTRIC CURRENT THROUGH GASESEXERCISE - Short answer
6 Videos
- ELECTROMAGNETIC INDUCTIONBOOK - HC VERMA ENGLISHCHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - Questions for short answer
9 Videos
Similar Questions
Knowledge Check
In the rectangular coordinate system shown, ABCD is a parallogram. If the coordinates of the points A,B,C and D are (0,2),(a,b),(a,2) and (0,0), respectively, then b =
 A0B2C3D4
A0B2C3D4If a circle passes through the point (0,0), (a,0) and (0,b), then the coordinates of its centre are
A(a,b)B(−a2,−b2)C(a2,b2)D(-a, -b)
Consider a circles S with centre at the origin and radius 4. Four circles A, B, C and D each with radius unity and centres (−3,0),(−1,0),(1,0) and (3,0) respectively are drawn. A chord PQ of the circle S and passes through the centre of the circle C. If the length of this chord can be expressed as √x , find x.
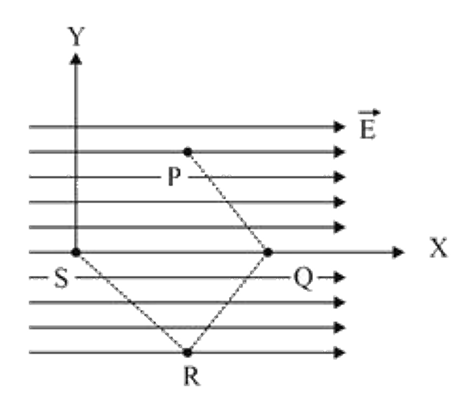
View SolutionPoint charge q moves from point P to point S along the path PQRS (figure shown) in a uniform electric field E pointing co-parallel to the positive direction of the x-axis. The coordinates of the points P, Q, R and S are (a,b,0),(2a,0,0),(a,−b,0)and(0,0,0) respectively. The work done by the field in the above process is given by the expression.
View SolutionIn a uniform electric field, the potential is 10V at the origin of coordinates , and 8V at each of the points (1, 0, 0), (0, 1, 0) and (0, 0, 1). The potential at the point (1, 1,1 ) will be .
View SolutionIf a circle passes through the points (0,0),(a,0)and(0,b), then find the coordinates of its centre.
View SolutionA circle having its centre in the first quadrant touches the y-axis at the point (0,2) and passes through the point (1,0). Find the equation of the circle
View SolutionTwo point charges q and –q are at positions (0,0,d) and (0,0, –d) respectively . What is the electric field at (a,0,0 ) ?
View Solution
