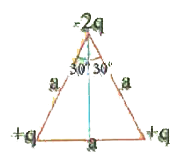
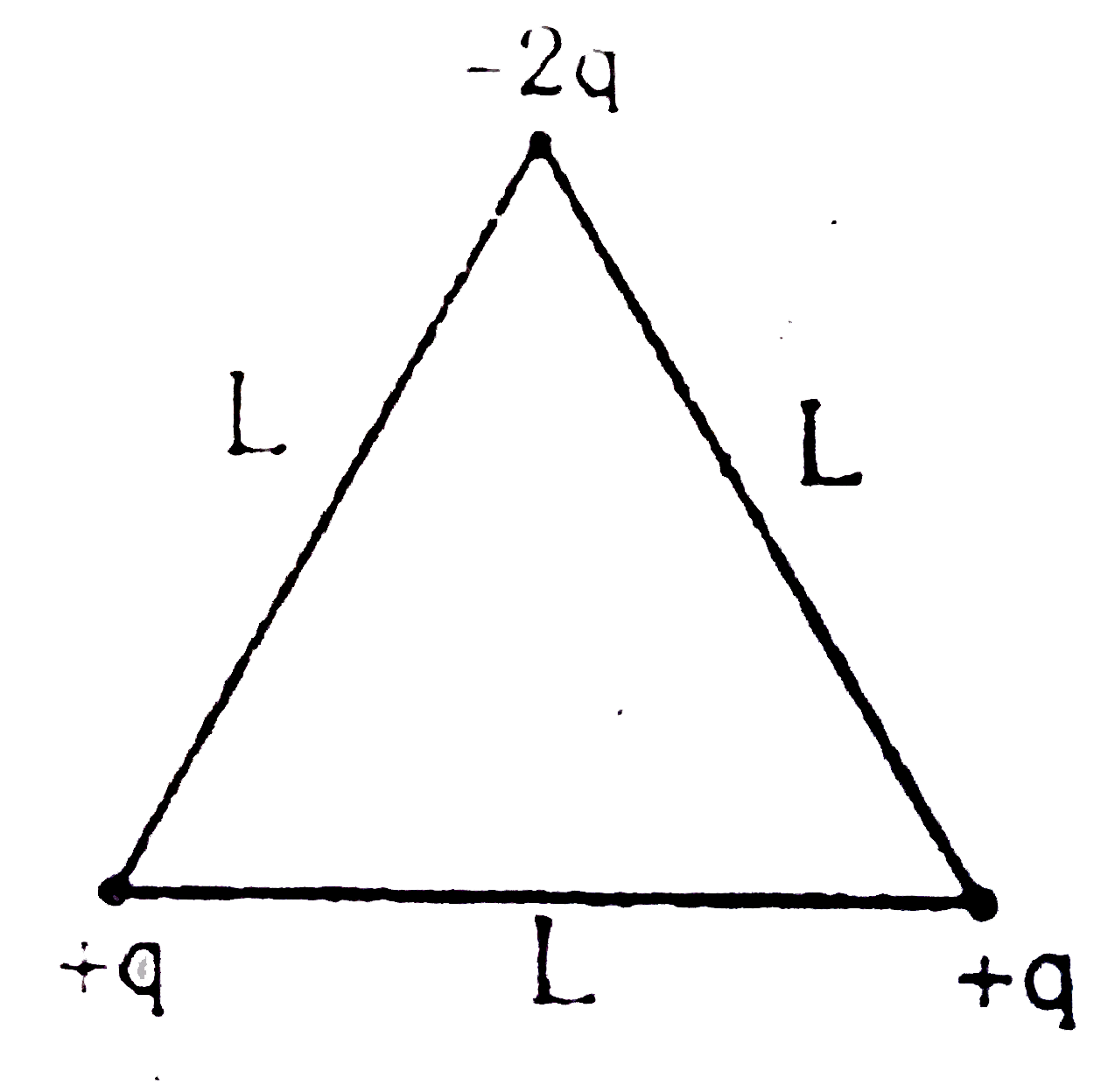
Three charges are arranged on the vertices of an equilateral triangle as shown in figure (29.E6) find the dipole moment of the combination.

Let−qand−qareplacedatAandC
where 2q on B
So,≤n>hofA=d
So, thedipo≤moment=(q×d)=P
So, resultant dipole moment
P=[(qd)2+(qd)2+2qdqdcos60]12
=[d2q2+d2q2+2d2q2×12]12
=[3q2d2]12=√3qd
Topper's Solved these Questions
- BOOK - HC VERMA ENGLISHCHAPTER - ELECTRIC FIELD AND POTENTIALEXERCISE - question for short answer14videos
ELECTRIC FIELD AND POTENTIAL
- BOOK - HC VERMA ENGLISHCHAPTER - ELECTRIC FIELD AND POTENTIALEXERCISE - Objective 19videos
ELECTRIC FIELD AND POTENTIAL
- BOOK - HC VERMA ENGLISHCHAPTER - ELECTRIC FIELD AND POTENTIALEXERCISE - worked out Examples19videos
ELECTRIC FIELD AND POTENTIAL
- BOOK - HC VERMA ENGLISHCHAPTER - ELECTRIC CURRENT THROUGH GASESEXERCISE - Short answer6videos
ELECTRIC CURRENT THROUGH GASES
- BOOK - HC VERMA ENGLISHCHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - Questions for short answer9videos
ELECTROMAGNETIC INDUCTION
Similar Questions
Knowledge Check
- Question 1 - Select One
Three charges of (+2q),(−q) and (−q) are placed at the corners A,B and C of an equilateral triangle of side a as shown in the adjoining figure. Then the dipole moment of this combination is
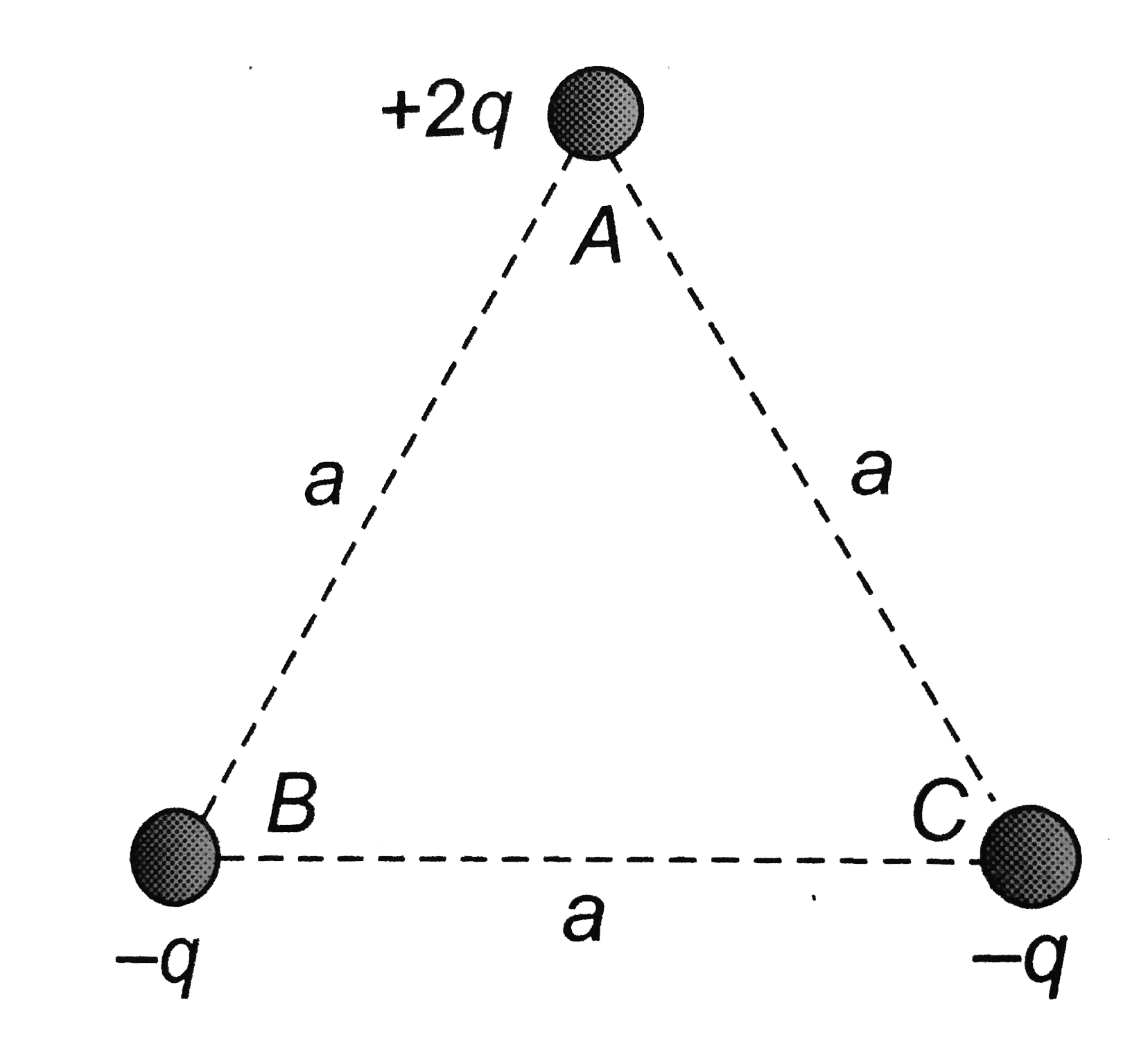 AqaBZeroCqa√3D2√3qa
AqaBZeroCqa√3D2√3qa - Question 2 - Select One
Three charges are placed at the vertices of an equilateral trianlge of side a as shown in the following figure. The force experienced by the charge placed at the vertex A in a direction normal to BC is
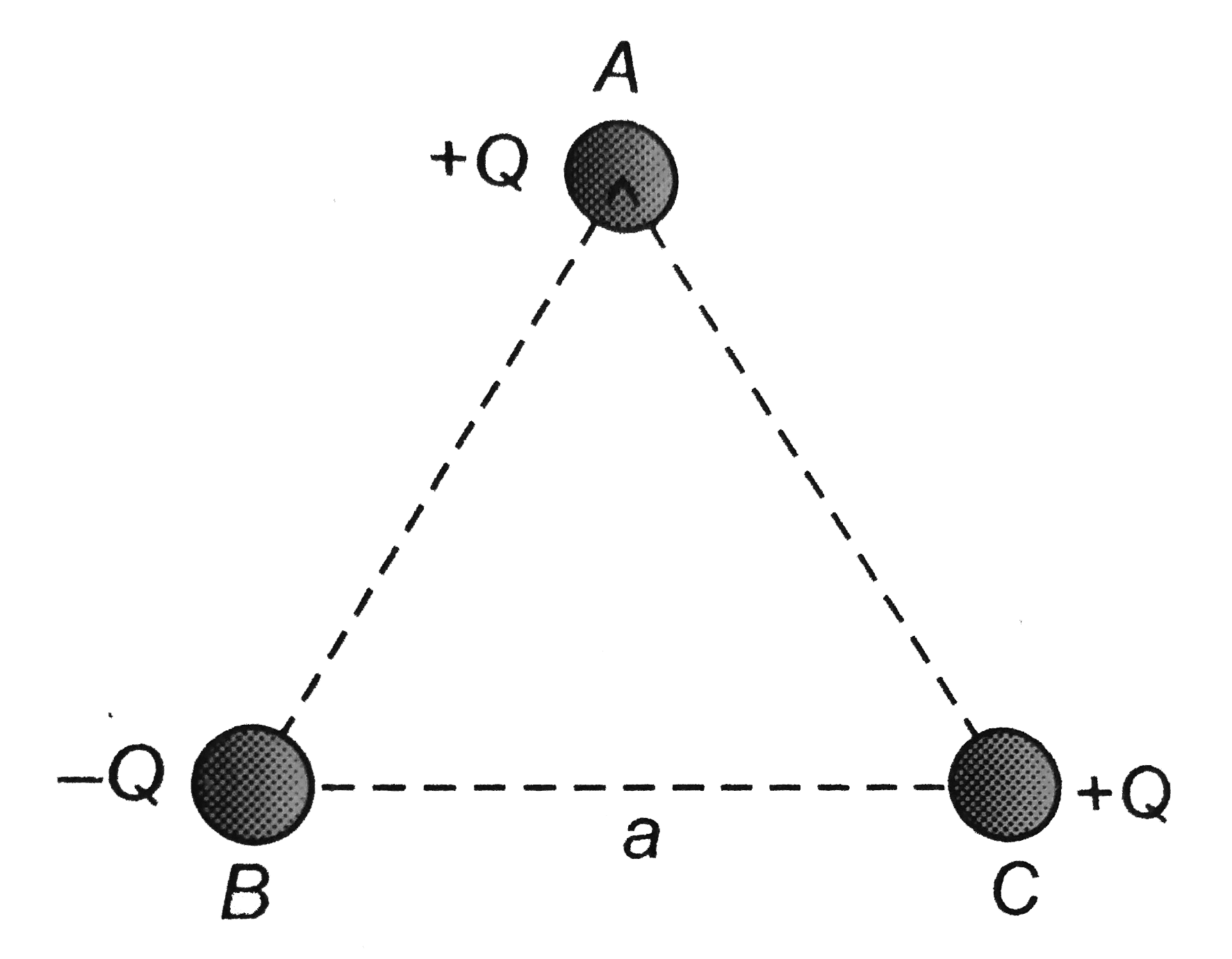 AQ24πε0a2B−Q24πε0a2CzeroDQ22πε0a2
AQ24πε0a2B−Q24πε0a2CzeroDQ22πε0a2
Find the coordinates of the vertices of an equilateral triangle of side 2a as shown in Figure.
View SolutionThree charges are placed at the vertex of an equilateral triangle as shown in figure. The value of Q, for which the electrostatic potential energy of the system is zero, is
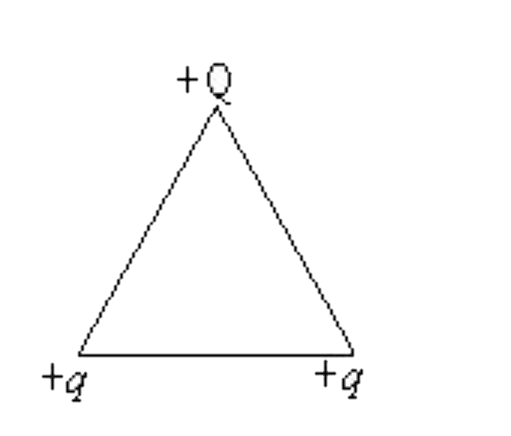 View Solution
View SolutionThree points charges are placed at the corners of an equilateral triangle of side L as shown in the figure:
 View Solution
View SolutionThree charges of (+2q),(−q) and (−q) are placed at the corners A,B and C of an equilateral triangle of side a as shown in the adjoining figure. Then the dipole moment of this combination is
 View Solution
View SolutionThree identical positive charges Q are arranged at the vertices of an equilateral triangle. The side of the triangle is a. Find the intensity of the field at the vertex of a regular tetrahedron of which the triangle is the base.
View SolutionThree identical positive charges Q are arranged at the vertices of an equilateral triangle. The side of the triangle is a. Find the intensity of the field at the vertex of a regular tetrahedron of which the triangle is the base.
View Solution