A cylindrical capacitor is constructed using two coaxial cylinders of the same length 10cm of radii 2mm and 4mm. (a) calculate the capacitance (b) another capacitor of the same length is constructed with cylinders of radii 4mm and 8mm. Calculate the capacitance .
To solve the problem of calculating the capacitance of two cylindrical capacitors, we will follow these steps:
Given Data:
1. Length of both capacitors, l=10cm=0.1m
2. For the first capacitor:
- Inner radius, a=2mm=0.002m
- Outer radius, b=4mm=0.004m
3. For the second capacitor:
- Inner radius, a=4mm=0.004m
- Outer radius, b=8mm=0.008m
Formula for Capacitance of a Cylindrical Capacitor:
The capacitance C of a cylindrical capacitor can be calculated using the formula:
C=2πϵ0lln(b/a)
where:
- ϵ0 is the permittivity of free space, ϵ0≈8.85×10−12F/m
- l is the length of the capacitor
- b is the outer radius
- a is the inner radius
(a) Calculate the Capacitance for the First Capacitor:
1. Substituting the values into the formula:
C1=2π(8.85×10−12)(0.1)ln(0.004/0.002)
2. Calculate the natural logarithm:
ln(0.004/0.002)=ln(2)≈0.693
3. Plugging in the values:
C1=2π(8.85×10−12)(0.1)0.693
4. Calculating the capacitance:
C1≈5.57×10−120.693≈8.04×10−12F
5. Converting to picoFarads:
C1≈8.04pF≈8pF
(b) Calculate the Capacitance for the Second Capacitor:
1. Using the same formula:
C2=2π(8.85×10−12)(0.1)ln(0.008/0.004)
2. Calculate the natural logarithm:
ln(0.008/0.004)=ln(2)≈0.693
3. Plugging in the values:
C2=2π(8.85×10−12)(0.1)0.693
4. Calculating the capacitance:
C2≈5.57×10−120.693≈8.04×10−12F
5. Converting to picoFarads:
C2≈8.04pF≈8pF
Final Answers:
- (a) The capacitance of the first capacitor is approximately 8pF.
- (b) The capacitance of the second capacitor is also approximately 8pF.
1. Length of both capacitors, l=10cm=0.1m
2. For the first capacitor:
- Inner radius, a=2mm=0.002m
- Outer radius, b=4mm=0.004m
3. For the second capacitor:
- Inner radius, a=4mm=0.004m
- Outer radius, b=8mm=0.008m
The capacitance C of a cylindrical capacitor can be calculated using the formula:
C=2πϵ0lln(b/a)
where:
- ϵ0 is the permittivity of free space, ϵ0≈8.85×10−12F/m
- l is the length of the capacitor
- b is the outer radius
- a is the inner radius
1. Substituting the values into the formula:
C1=2π(8.85×10−12)(0.1)ln(0.004/0.002)
ln(0.004/0.002)=ln(2)≈0.693
C1=2π(8.85×10−12)(0.1)0.693
C1≈5.57×10−120.693≈8.04×10−12F
C1≈8.04pF≈8pF
1. Using the same formula:
C2=2π(8.85×10−12)(0.1)ln(0.008/0.004)
ln(0.008/0.004)=ln(2)≈0.693
C2=2π(8.85×10−12)(0.1)0.693
C2≈5.57×10−120.693≈8.04×10−12F
C2≈8.04pF≈8pF
- (a) The capacitance of the first capacitor is approximately 8pF.
- (b) The capacitance of the second capacitor is also approximately 8pF.
Topper's Solved these Questions
- CAPACITORSBOOK - HC VERMA ENGLISHCHAPTER - CAPACITORSEXERCISE - short answer
7 Videos
- CAPACITORSBOOK - HC VERMA ENGLISHCHAPTER - CAPACITORSEXERCISE - OBJECTIVE 2
6 Videos
- BOHR'S MODEL AND PHYSICS OF THE ATOMBOOK - HC VERMA ENGLISHCHAPTER - BOHR'S MODEL AND PHYSICS OF THE ATOMEXERCISE - Short Answer
10 Videos
- DISPERSION AND SPECTRABOOK - HC VERMA ENGLISHCHAPTER - DISPERSION AND SPECTRAEXERCISE - Question for short Answer
6 Videos
Similar Questions
A cylindrical capacitor has has two co-axial cylinders of length 20 cm and radii 2r and r, inner cylinder is gliven a charge 10 μC and and outer cylinder a charge of - 10 μC. the potential difference between the two cylinders will be
View SolutionCalculate the capacitance of a parallel-plate capacitor having 20 cm x 20 cm square plates deparated by a distance of 1.0 mm.
View Solution
Knowledge Check
A cylindrical capacitor has two co-axial cylinders of length 20 cm and radii 1.5 cm and 1.6 cm. The outer cylinder is earthed and inner cylinder is given a charge 4μC. The capacitance of the system is (neglect end effect)
A2.8×10−8FB4.2×10−14FC1.7×10−10FD3.4×10−12F
Two wires of the same material and same length have radii 1 mm and 2 mm respectively. Compare :
their specific resistance.
View SolutionTwo wires of the same material and same length have radii 1 mm and 2 mm respectively. Compare :
their resistances,
View SolutionThe lengths of two steel wires are 100 cm and 200cm and their radii are 6 and 3 mm. nder the same stretching force, what is the ratio of the elongations produced in them.
View SolutionCalculate the ratio of capacitance of two capacitors of same dimensions but of different values K and K4 arranged in two ways as shown in Fig. (i) and (ii).

View SolutionA cylinder whose height is two thirds of its diameter, has the same volume as a sphere of radius 4cm. Calculate the radius of the base of the cylinder.
View SolutionA sphercial capacitor is made of two conducting spherical shells of radii a and b.The space between the shells is filled with a dielectric constant Kup to a radius c as shown in figure. Calculate the capacitance .
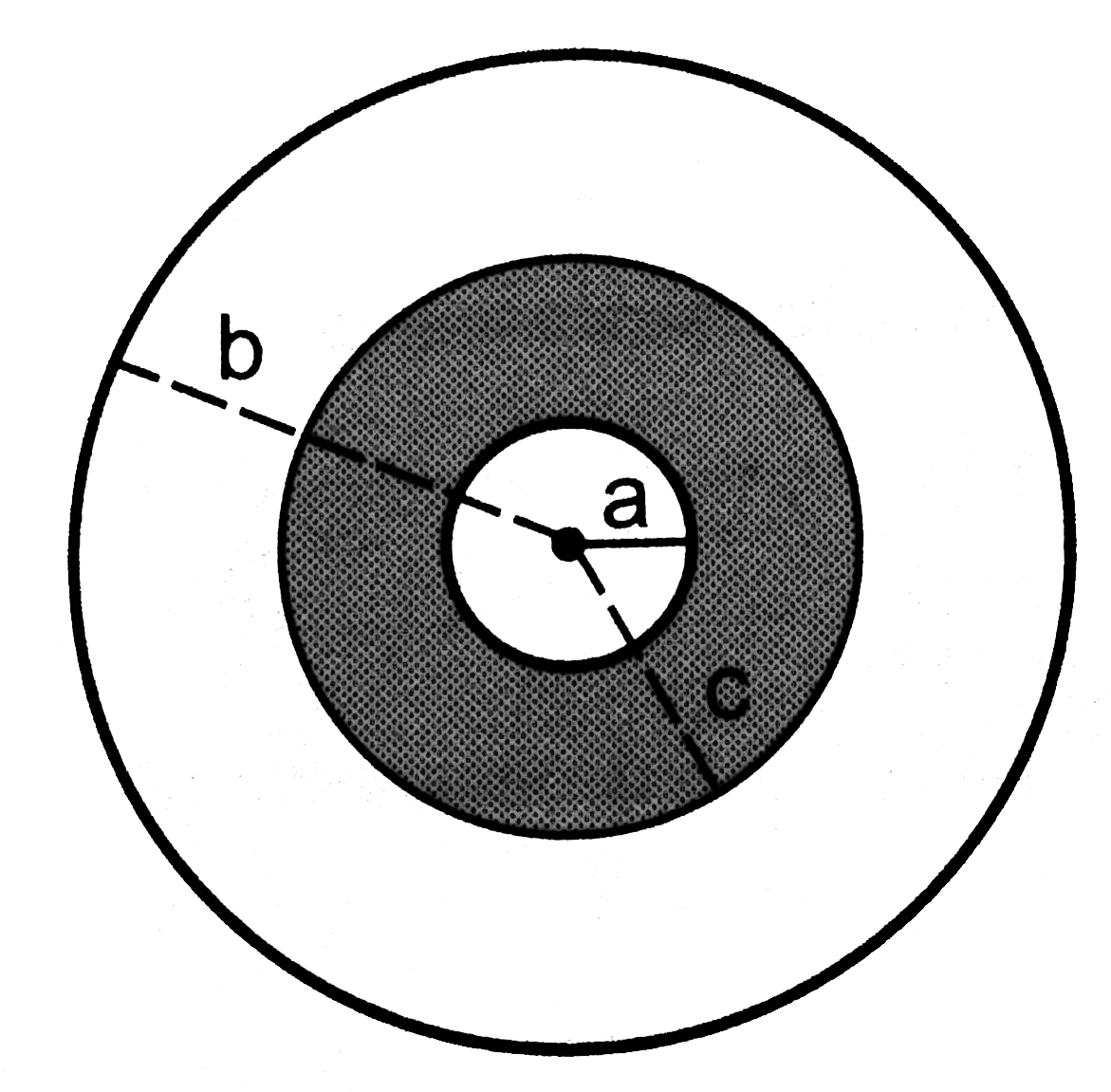
View SolutionIn a parallel plate capacitor with air between the plates, each plate has an area of 6×10−3m2 and distance between the plates is 3mm. Calculate the capacitance. If this capacitance is connected to a 100V supply, what is the charge on each plate of the capacitor ?
View Solution
