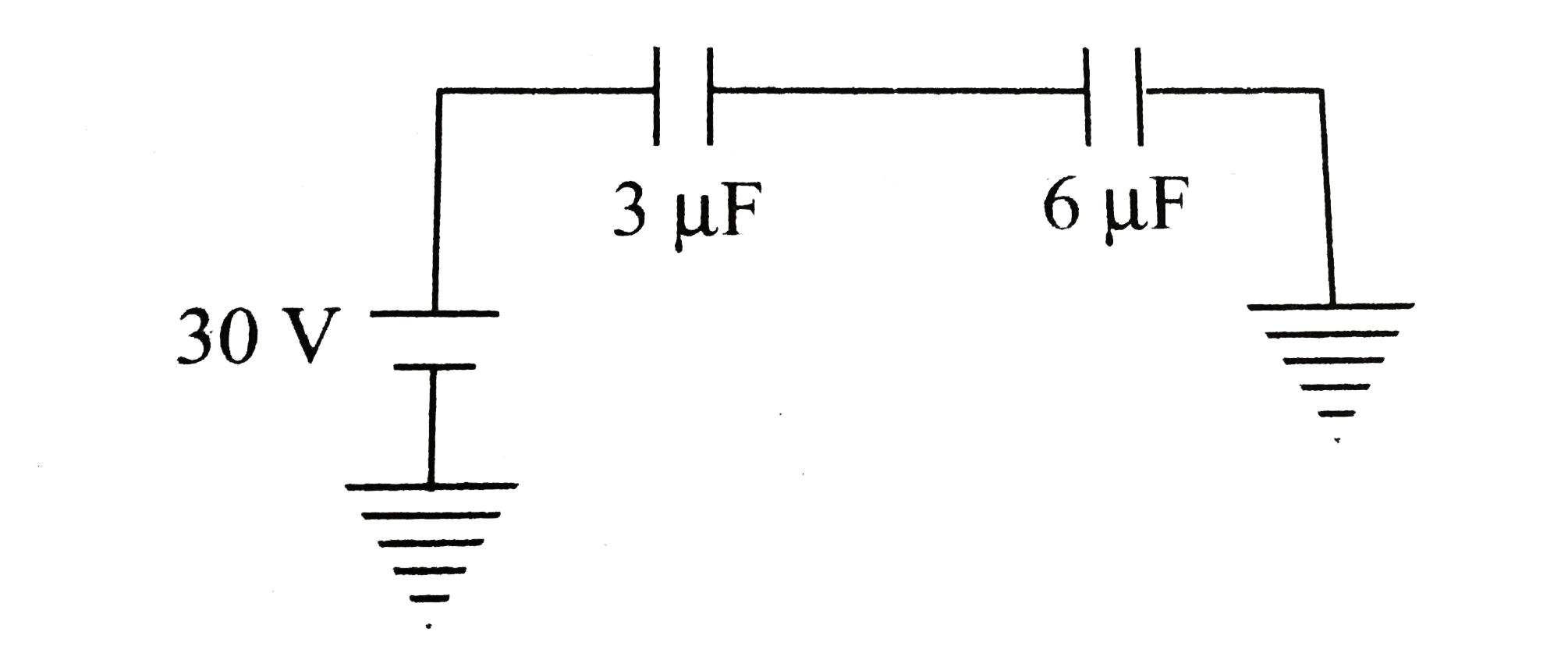
In the circuit shown in figure, the charge stored on a capacitor of capacitance 3μF is
zero
40μC
60μC
90μC
The correct Answer is:C
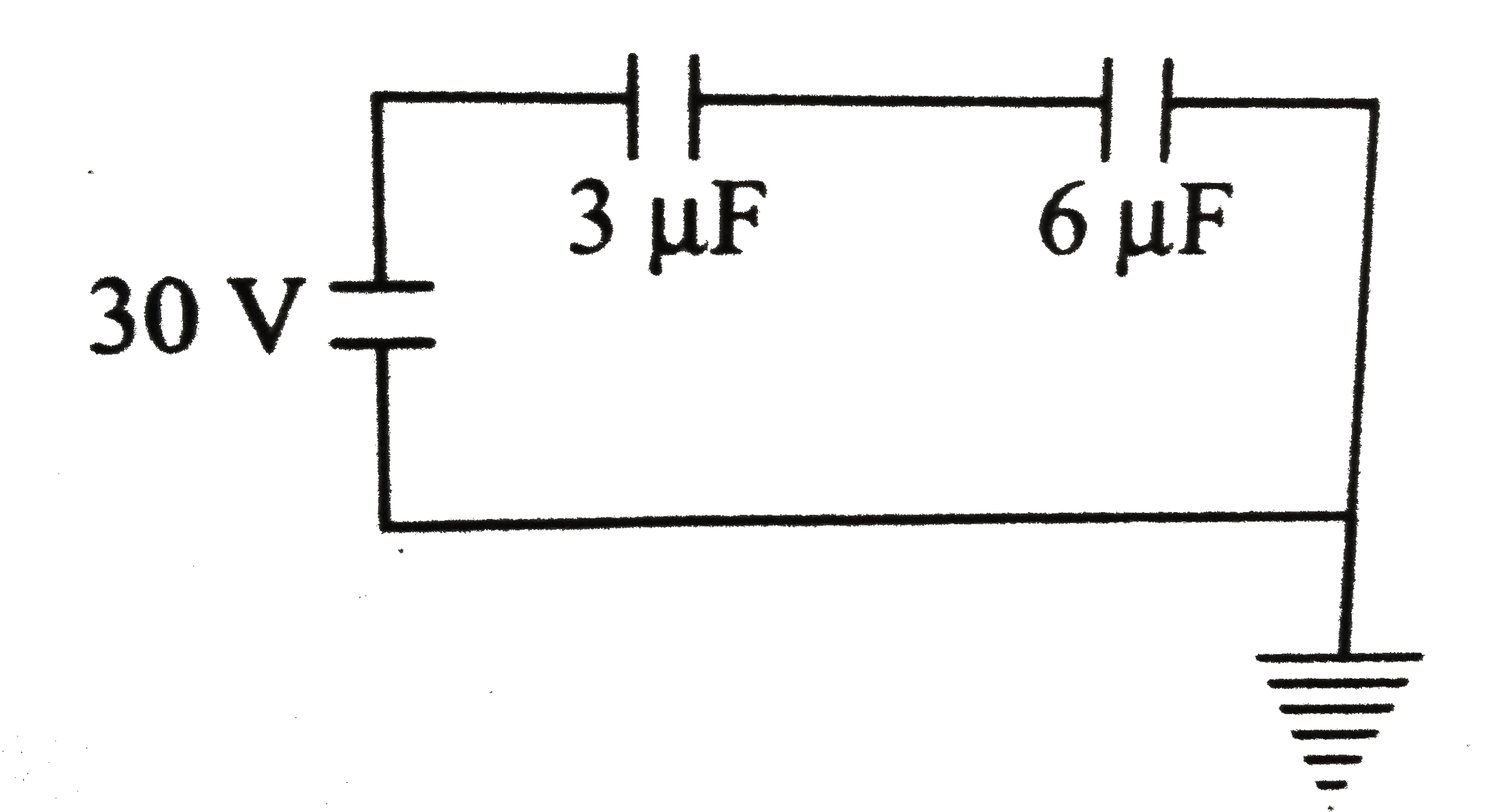
Circuit is redrawn as shown in Fig. SA1.21. Equvalent capacity of combination is
Caq=3×69=2μF
Hence, charge
q=CeqV=2μF×30V=60μC
Topper's Solved these Questions
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - MISCELLANEOUS VOLUME 3EXERCISE - Assertion and Reason Type8videos
MISCELLANEOUS VOLUME 3
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - MISCELLANEOUS VOLUME 3EXERCISE - Comprehension Type94videos
MISCELLANEOUS VOLUME 3
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - MAGNETIC FIELD AND MAGNETIC FORCESEXERCISE - Multiple Correct Answer type2videos
MAGNETIC FIELD AND MAGNETIC FORCES
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - MISCELLANEOUS VOLUME 5EXERCISE - Integer12videos
MISCELLANEOUS VOLUME 5
Similar Questions
In the circuit shown in figure charge stored in the capacitor of capacity 5μf is
View SolutionIn the ciruit shown in, C=6μF. The charge stored in the capacitor of capacity C is
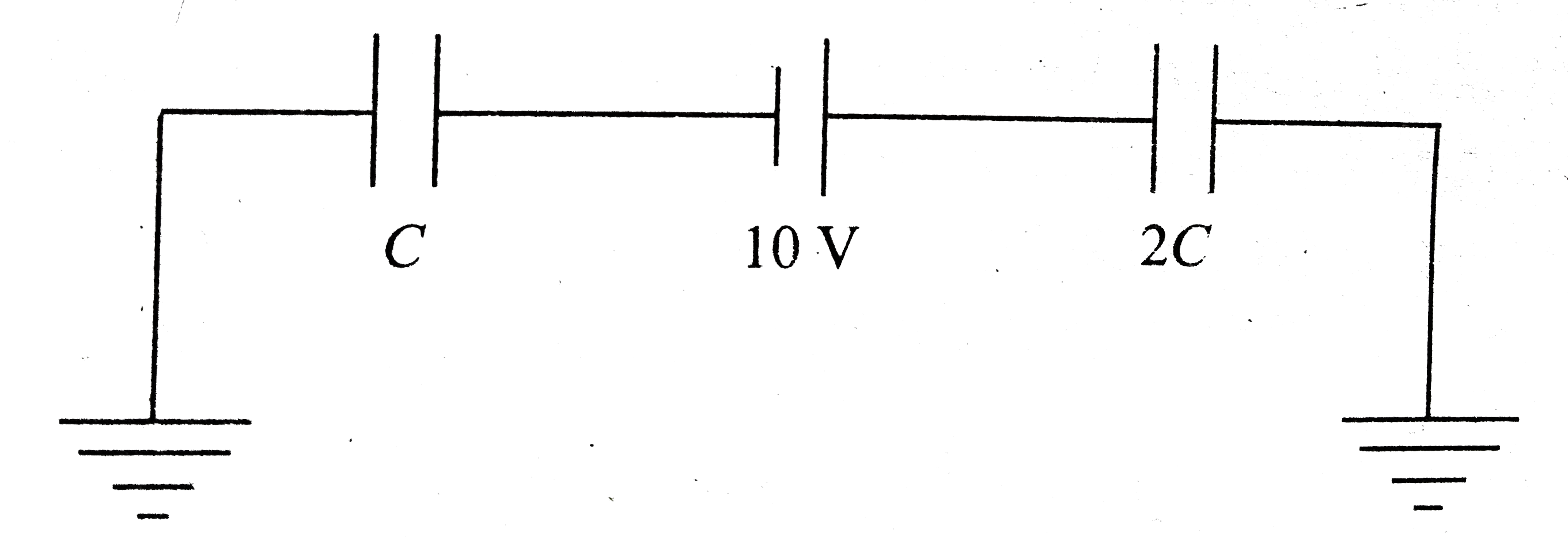. View SolutionIn the ciruit shown in, C=6μF. The charge stored in the capacitor of capacity C is
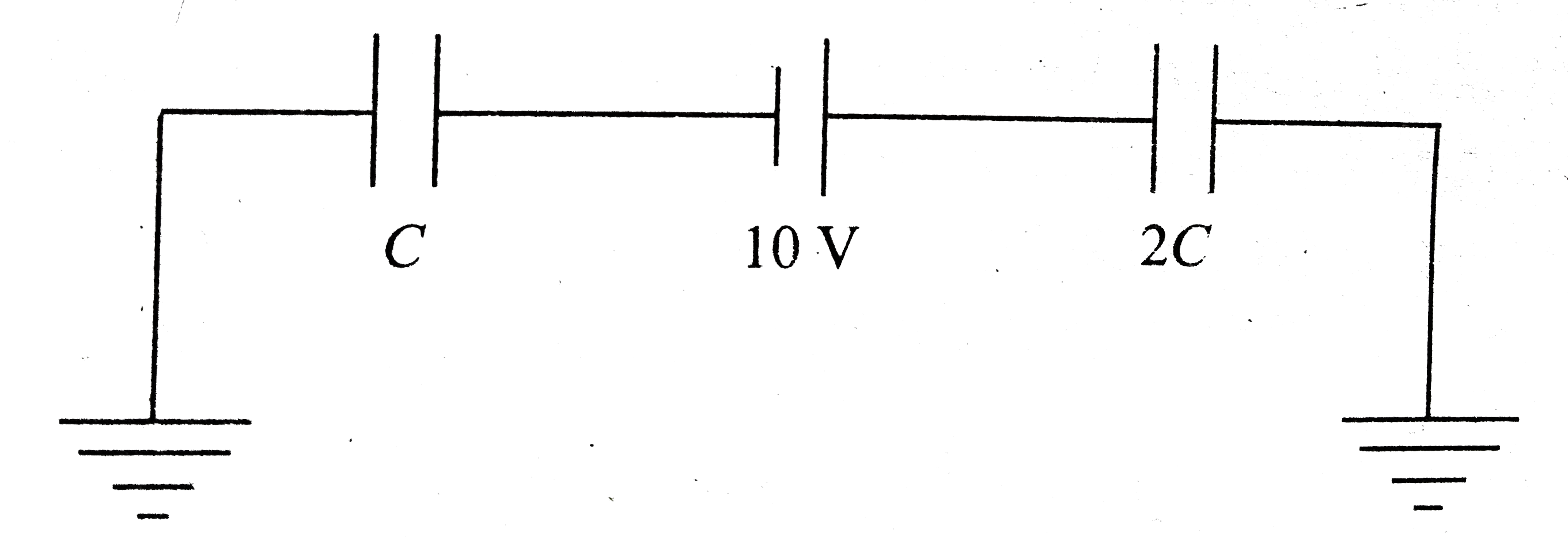. View SolutionIn the circuit as shown in figure, energy stored in capacitor at steady state is
View SolutionIn the circuit shown below, the charge on the 60μF capacitor is
View SolutionFor the circuit shown in the figure, find the charge stored on capacitor in steady state.
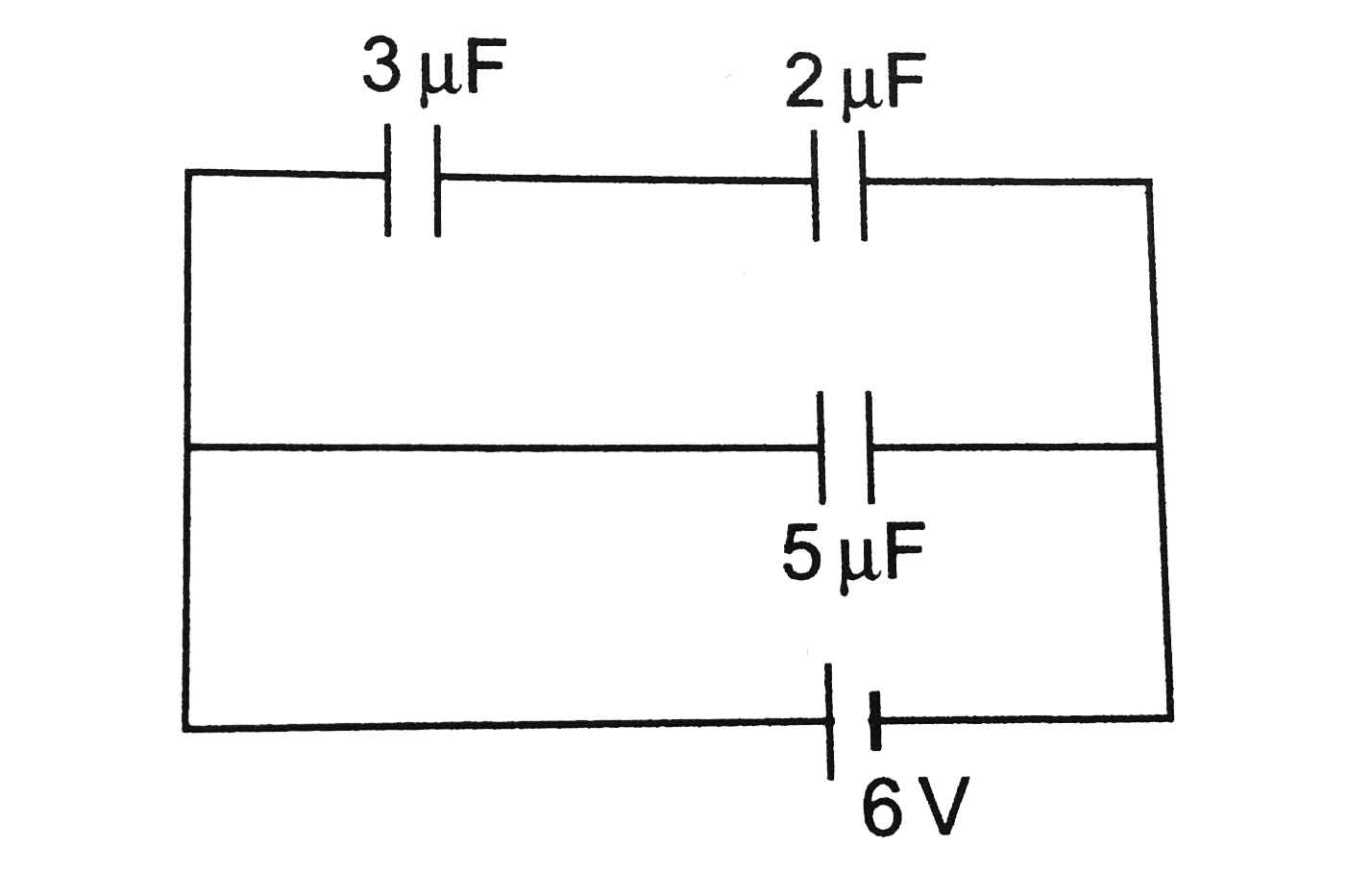
View SolutionIn the circuit shown in figure, the ratio of charge on 5μF and 2μF capacitor is
View SolutionIn the circuit shown in figure. Charge stored in 6μF capacitor will be (C=6μF)
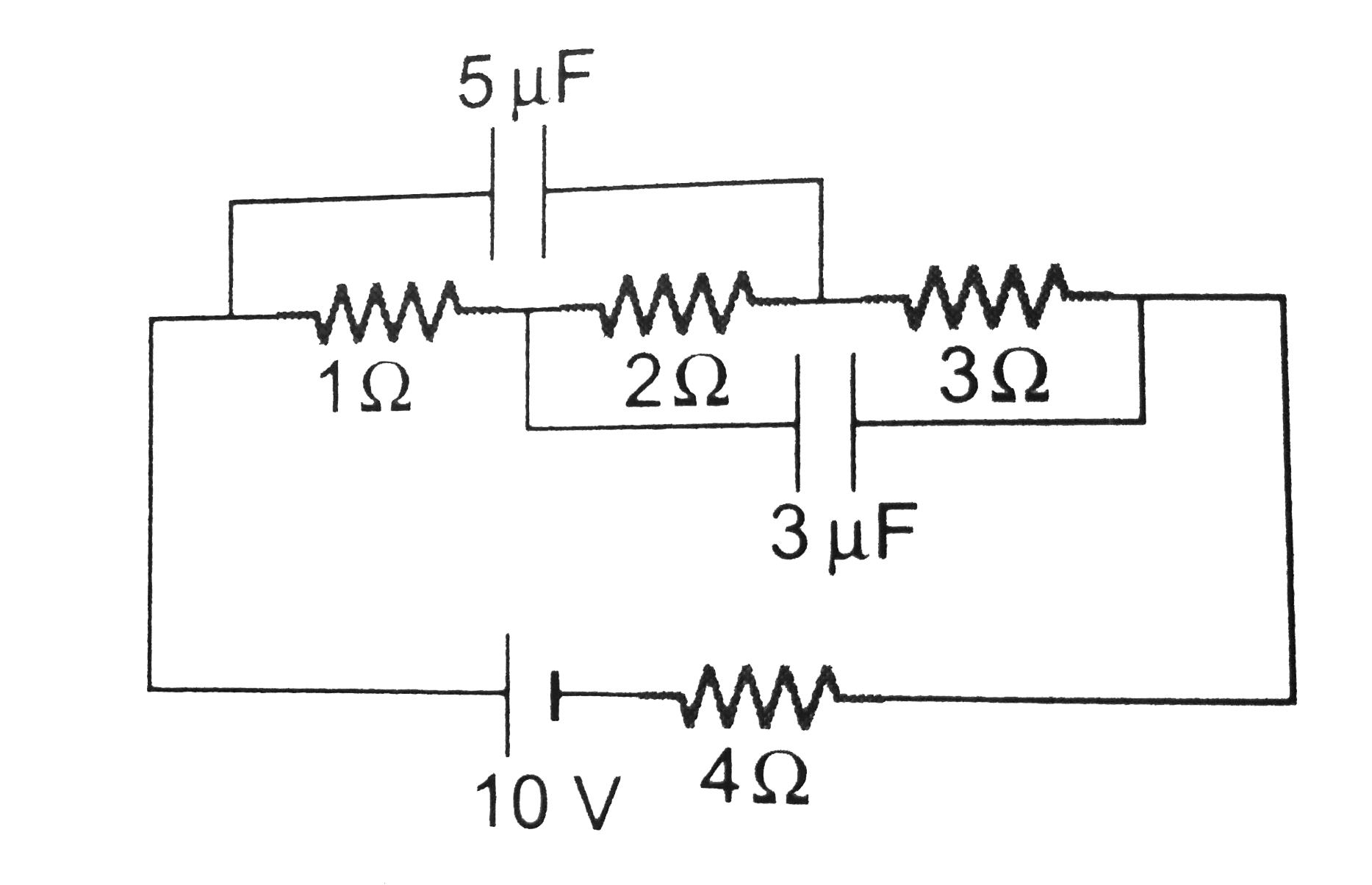
View SolutionIn the shown network, find the charges on capacitors of capacitances 5μF and 3μF, in steady state.
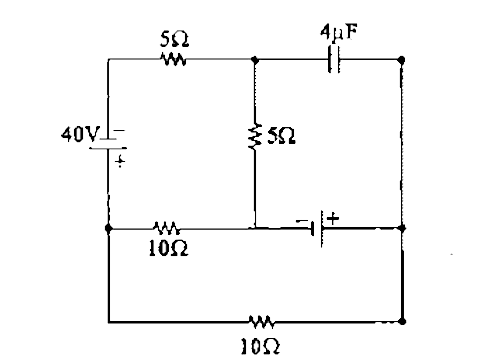
View SolutionIn the circuit shown in figure 3.141, find the energy stored in 4μF capacitor in steady state.
View Solution