A capacitor having a capacitance of 100μf is changed to a potential difference of 50V.(a) What is the magnitude of the charge on each plate? (b)The charging battery is disconnected and a dielectric of dielectric constant 2.5 is inserted . Calculate the new potential difference between the plate .
To solve the problem step by step, we will break it down into two parts as given in the question.
Part (a): Finding the Magnitude of the Charge on Each Plate
1. Identify the Given Values:
- Capacitance, C=100μF=100×10−6F
- Potential difference, V=50V
2. Use the Formula for Charge:
The charge Q on the capacitor can be calculated using the formula:
Q=C×V
3. Substitute the Values:
Q=(100×10−6F)×(50V)
4. Calculate the Charge:
Q=100×50×10−6=5000×10−6C=5×10−3C
Thus, the magnitude of the charge on each plate is:
Q=5mC
Part (b): Finding the New Potential Difference After Inserting the Dielectric
1. Identify the Dielectric Constant:
- Dielectric constant, k=2.5
2. Calculate the New Capacitance:
The new capacitance C′ when a dielectric is inserted is given by:
C′=k×C
Substituting the values:
C′=2.5×(100×10−6F)=250×10−6F
3. Use the Charge from Part (a):
The charge Q remains the same as the battery is disconnected:
Q=5×10−3C
4. Calculate the New Potential Difference:
The new potential difference V′ across the plates can be calculated using:
V′=QC′
Substituting the values:
V′=5×10−3C250×10−6F
5. Calculate the New Potential Difference:
V′=5250×103=150×103=20V
Thus, the new potential difference between the plates after inserting the dielectric is:
V′=20V
Summary of Answers:
- (a) The magnitude of the charge on each plate is 5mC.
- (b) The new potential difference between the plates is 20V.
- Capacitance, C=100μF=100×10−6F
- Potential difference, V=50V
The charge Q on the capacitor can be calculated using the formula:
Q=C×V
Q=(100×10−6F)×(50V)
Q=100×50×10−6=5000×10−6C=5×10−3C
Thus, the magnitude of the charge on each plate is:
Q=5mC
- Dielectric constant, k=2.5
The new capacitance C′ when a dielectric is inserted is given by:
C′=k×C
Substituting the values:
C′=2.5×(100×10−6F)=250×10−6F
The charge Q remains the same as the battery is disconnected:
Q=5×10−3C
The new potential difference V′ across the plates can be calculated using:
V′=QC′
Substituting the values:
V′=5×10−3C250×10−6F
V′=5250×103=150×103=20V
V′=20V
- (a) The magnitude of the charge on each plate is 5mC.
- (b) The new potential difference between the plates is 20V.
Topper's Solved these Questions
- BOOK - HC VERMA ENGLISHCHAPTER - CAPACITORSEXERCISE - short answer7videos
CAPACITORS
- BOOK - HC VERMA ENGLISHCHAPTER - CAPACITORSEXERCISE - OBJECTIVE 26videos
CAPACITORS
- BOOK - HC VERMA ENGLISHCHAPTER - BOHR'S MODEL AND PHYSICS OF THE ATOMEXERCISE - Short Answer10videos
BOHR'S MODEL AND PHYSICS OF THE ATOM
- BOOK - HC VERMA ENGLISHCHAPTER - DISPERSION AND SPECTRAEXERCISE - Question for short Answer6videos
DISPERSION AND SPECTRA
Similar Questions
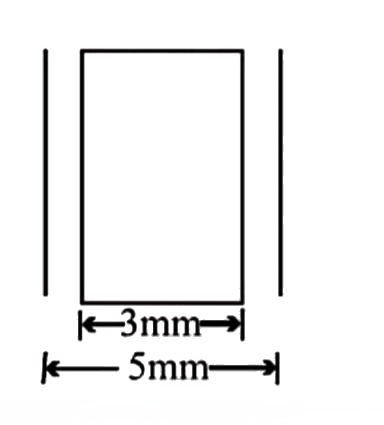
Separation between the plates of parallel plate capacitor is 5 mm. this capacitor, having air as the dielectric medium between the plates, is charged to a potential difference 25 V using a battery. The battery is then disconnected and a dielectric slab of thickness 3mm and dielectric constant K=10 is placed between the plates as shown. potential difference between the plates after the dielectric slab has been introduced is-
 View Solution
View SolutionA parallel plate capacitor having capacitance 12pF is charged bya battery to a potential difference of 10V between its plates. The charging battery is now disonnected and a porcelain slab of dielectric constant 6.5 is slipped between the plates. The work done by the capacitor on the slab is
View Solution
Knowledge Check
- Question 1 - Select One
A parallel plate air capacitor is charged to a potential difference of V volts. After disconnecting the charging battery the distance between the plates of the capacitor is increased using an isulating handle. As a result the potential difference between the plates
AincreasesBdecreaseCdoes not chargeDbecomes zero
A capacitor with plate separation d is charged to V volts. The battry is disconnected and a dielectric slab of thickness d2 and dlelectric constant '2' is inserted between the plates. The potential difference across its terminals becomes
View SolutionFigure shows a parallel plate capacitor with plate area A and plate separation d. A potential difference is being applied between the plates. The battery is then disconnected and a dielectric slab of dieletric constant K is placed in between the plates of the capacitor as shown.

The electric field in the gaps between the plates and the electric slab will beView SolutionTwo parallel plate capacitors of capacitances C and 2C are connected in parallel and charged to a potential difference V. The battery is then disconnected and the region between the plates of the capacitor C is completely filled with a material of dielectric constant K. The potential differences across the capacitors now becomes...........
View SolutionThe potential enery of a charged parallel plate capacitor is U0. If a slab of dielectric constant K is inserted between the plates, then the new potential energy will be
View SolutionThe potential enery of a charged parallel plate capacitor is U0. If a slab of dielectric constant K is inserted between the plates, then the new potential energy will be
View SolutionA parallel plate air capacitor is charged to a potential difference of V volts. After disconnecting the charging battery the distance between the plates of the capacitor is increased using an isulating handle. As a result the potential difference between the plates
View SolutionA parallel plate air capacitor is charged to a potential difference of V volts. After disconnecting the charging battery the distance between the plates of the capacitor is increased using an isulating handle. As a result the potential difference between the plates
View Solution

