Is work dome by a battery always equal to the thermal energy develop in electrical circuits? What happens if a capacitor is connected in the circuit?
To answer the question, "Is work done by a battery always equal to the thermal energy developed in electrical circuits? What happens if a capacitor is connected in the circuit?", we will analyze the situation step by step.
Step 1: Understanding Work Done by the Battery
The work done by a battery in an electrical circuit is the energy supplied by the battery to move charges through the circuit. This work can be calculated using the formula:
W=Q⋅V
where W is the work done, Q is the charge, and V is the voltage (or electromotive force, EMF) of the battery.
Step 2: Thermal Energy in the Circuit
In a circuit, the work done by the battery can be converted into thermal energy due to the resistances present in the circuit. The thermal energy developed in the circuit can be expressed as:
Q=I2⋅R⋅t
where I is the current, R is the resistance, and t is the time for which the current flows.
Step 3: Non-Ideal vs. Ideal Battery
- Non-Ideal Battery: In the case of a non-ideal battery, there is internal resistance (let's denote it as r). The total thermal energy developed will be the sum of the thermal energy in the internal resistance and the external resistance:
W=I2⋅(R+r)⋅t
Here, the work done by the battery is equal to the thermal energy developed in both resistances.
- Ideal Battery: In the case of an ideal battery, there is no internal resistance. Therefore, the work done by the battery is equal to the thermal energy developed only in the external resistance R:
W=I2⋅R⋅t
Step 4: Effect of Connecting a Capacitor
When a capacitor is connected in the circuit, the scenario changes:
- The energy supplied by the battery is stored in the capacitor and can be calculated as:
U=12CV2
where U is the energy stored in the capacitor, C is the capacitance, and V is the voltage across the capacitor.
- In this case, when the capacitor charges, half of the energy supplied by the battery is stored in the capacitor, and the other half is dissipated as thermal energy in the circuit (due to resistances):
Energy supplied by battery=U+Thermal Energy
W=12CV2+12CV2
Conclusion
1. The work done by a battery is not always equal to the thermal energy developed in the circuit. It depends on whether the battery is ideal or non-ideal.
2. When a capacitor is connected, the energy supplied by the battery is divided between the energy stored in the capacitor and the thermal energy dissipated in the circuit.
The work done by a battery in an electrical circuit is the energy supplied by the battery to move charges through the circuit. This work can be calculated using the formula:
W=Q⋅V
where W is the work done, Q is the charge, and V is the voltage (or electromotive force, EMF) of the battery.
In a circuit, the work done by the battery can be converted into thermal energy due to the resistances present in the circuit. The thermal energy developed in the circuit can be expressed as:
Q=I2⋅R⋅t
where I is the current, R is the resistance, and t is the time for which the current flows.
- Non-Ideal Battery: In the case of a non-ideal battery, there is internal resistance (let's denote it as r). The total thermal energy developed will be the sum of the thermal energy in the internal resistance and the external resistance:
W=I2⋅(R+r)⋅t
Here, the work done by the battery is equal to the thermal energy developed in both resistances.
W=I2⋅R⋅t
When a capacitor is connected in the circuit, the scenario changes:
- The energy supplied by the battery is stored in the capacitor and can be calculated as:
U=12CV2
where U is the energy stored in the capacitor, C is the capacitance, and V is the voltage across the capacitor.
Energy supplied by battery=U+Thermal Energy
W=12CV2+12CV2
1. The work done by a battery is not always equal to the thermal energy developed in the circuit. It depends on whether the battery is ideal or non-ideal.
2. When a capacitor is connected, the energy supplied by the battery is divided between the energy stored in the capacitor and the thermal energy dissipated in the circuit.
Topper's Solved these Questions
- ELECTRIC CURRENT IN CONDUCTORSBook:HC VERMA ENGLISHChapter:ELECTRIC CURRENT IN CONDUCTORSExercise:Exercises
Explore 84 Videos
- DISPERSION AND SPECTRABook:HC VERMA ENGLISHChapter:DISPERSION AND SPECTRAExercise:Question for short Answer
Explore 6 Videos
- ELECTRIC CURRENT THROUGH GASESBook:HC VERMA ENGLISHChapter:ELECTRIC CURRENT THROUGH GASESExercise:Short answer
Explore 6 Videos
Similar Questions
What is an electric circuit ?
View SolutionA nonideal battery is connected to a resistor. Is work done by thr battery equal to the hermal energy developed in the resistor?Does your answer change If the battery is ideal?
View SolutionFuse is connected in an electric circuit.
View SolutionFind total energy stored in capacitors given in the circuit
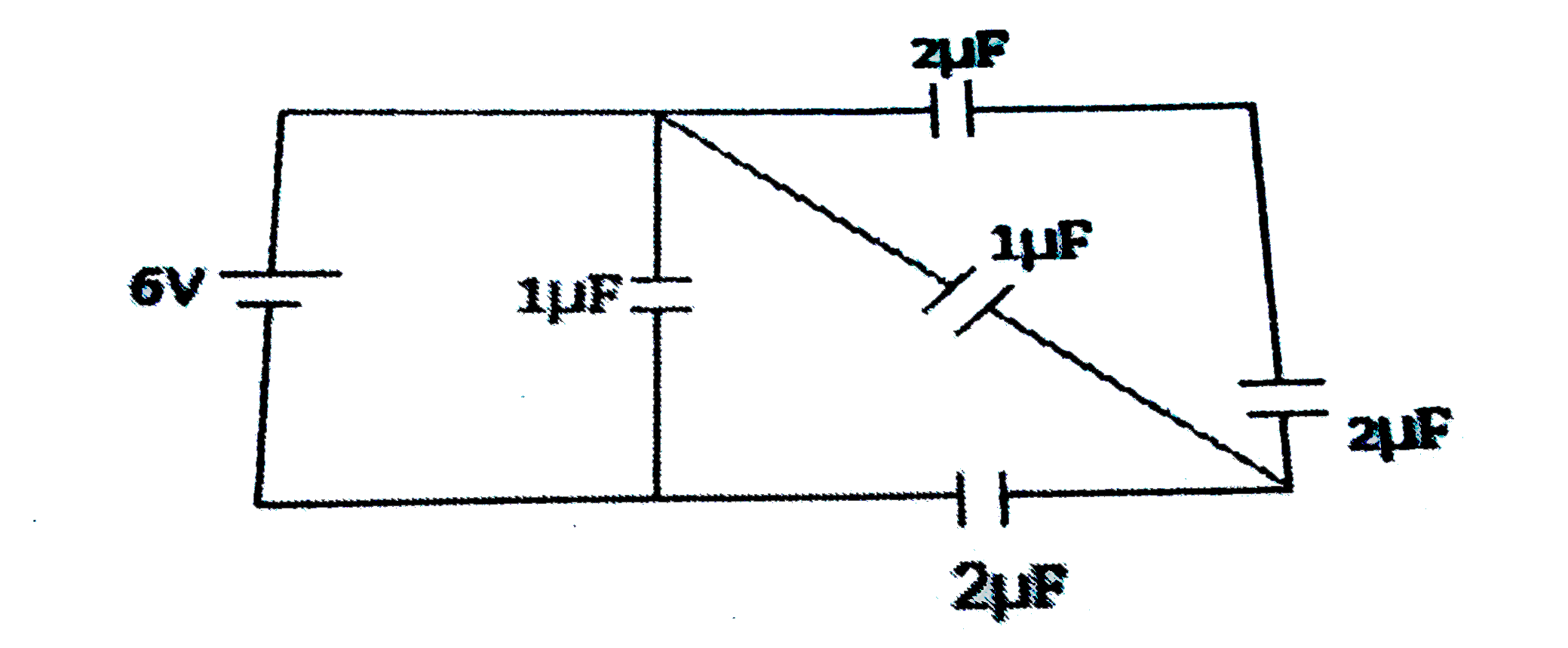
View SolutionDo "work done by the battery" and "the thermal energy developed"represent two names of the same physical quantity?
View SolutionFor the given circuit, the total energy stored in the circuit when a 12V battery is connected.(C=10μF)
_PHY_E05_125 _Q01.png)
View SolutionA student in a lab took a coil and connected it to a 12VDC source. He measures the steady state current in the circuit to be 4A. He then replaced the 12VDC source by a 12V,(ω=50rad/s)AC source and observes that the reading in the AC ammeter is 2.4A. He then decides to connect a 2500μF capacitor in series with the coil and calculate the average power developed in the circuit. Further he also decides to study the variation in current in the circuit (with the capacitor and the battery in series).
The power developed in te circuit when the capcitor of 2500 μF is connected in sereis with the coil is
View SolutionIn an electric circuit shown alongside, find
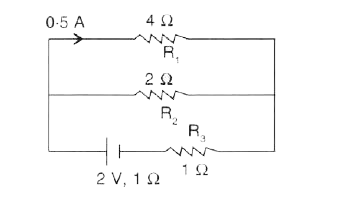
terminal voltage of the battery
View SolutionAn LC circuit contains a 20 mH inductor and a 50μF capacitor with an initial charge of 10 mC. The resistance of the circuit is negligible. Let the instant the circuit is closed be t = 0.
(a) What is the total energy stored initially ? Is it conserved during the oscillalions?
(b) What is the natural frequency of the circuit?
(c ) At what time is the energy stored? (i) Completely electrical ? (ii) Completely magnetic ?
(d) At what time is the total energy shared equally between the inductor and the capacitor ?
(e) If a resistor is inserted in the circuit, how much energy is eventually dissipated as heat ?
View SolutionA student in a lab took a coil and connected it to a 12VDC source. He measures the steady state current in the circuit to be 4A. He then replaced the 12VDC source by a 12V,(ω=50rads)AC source and observes that the reading in the AC ammeter is 2.4A. He then decides to connect a 2500μF capacitor in series with the coil and calculate the average power developed in the circuit. Further he also decides to study the variation in current in the circuit (with the capacitor and the battery in series).
Which of the following graph roughly matches the variation of current in the circuit (with the coil and capacitor connected in the series) when the angulr frequency is decreased from 50 rad/s to 25 rad/s?
View Solution