The thermal energy developed in a current-carrying resistor is given by U=I2Rt and also by U=VIt.should we say that U is proportional to I2or to I ?
To determine whether the thermal energy U developed in a current-carrying resistor is proportional to I2 or I, we will analyze the two given expressions for thermal energy.
Step 1: Analyze the first expression
The first expression for thermal energy is given by:
U=I2Rt
In this expression, U is expressed in terms of I2, R, and t. Here, R (resistance) and t (time) are constants when considering the thermal energy for a given resistor over a specific time period.
Step 2: Determine the proportionality from the first expression
From the first expression, we can see that:
U∝I2
This means that thermal energy U is proportional to the square of the current I.
Step 3: Analyze the second expression
The second expression for thermal energy is given by:
U=VIt
In this expression, U is expressed in terms of V (voltage), I (current), and t (time).
Step 4: Determine the relationship between V and I
According to Ohm's Law, the voltage V across a resistor is related to the current I and resistance R by:
V=IR
This indicates that V is dependent on I. Therefore, we cannot treat V as an independent variable when analyzing the proportionality of U in the second expression.
Step 5: Determine the proportionality from the second expression
Since V depends on I, we cannot directly conclude the proportionality of U from the second expression. However, if we substitute V in the second expression:
U=(IR)It=I2Rt
This brings us back to the first expression, confirming that:
U∝I2
Conclusion
Thus, we can conclude that the thermal energy U developed in a current-carrying resistor is proportional to I2 rather than I.
The first expression for thermal energy is given by:
U=I2Rt
In this expression, U is expressed in terms of I2, R, and t. Here, R (resistance) and t (time) are constants when considering the thermal energy for a given resistor over a specific time period.
From the first expression, we can see that:
U∝I2
This means that thermal energy U is proportional to the square of the current I.
The second expression for thermal energy is given by:
U=VIt
In this expression, U is expressed in terms of V (voltage), I (current), and t (time).
According to Ohm's Law, the voltage V across a resistor is related to the current I and resistance R by:
V=IR
This indicates that V is dependent on I. Therefore, we cannot treat V as an independent variable when analyzing the proportionality of U in the second expression.
Since V depends on I, we cannot directly conclude the proportionality of U from the second expression. However, if we substitute V in the second expression:
U=(IR)It=I2Rt
This brings us back to the first expression, confirming that:
U∝I2
Thus, we can conclude that the thermal energy U developed in a current-carrying resistor is proportional to I2 rather than I.
Topper's Solved these Questions
- ELECTRIC CURRENT IN CONDUCTORSBOOK - HC VERMA ENGLISHCHAPTER - ELECTRIC CURRENT IN CONDUCTORSEXERCISE - Exercises
84 Videos
- DISPERSION AND SPECTRABOOK - HC VERMA ENGLISHCHAPTER - DISPERSION AND SPECTRAEXERCISE - Question for short Answer
6 Videos
- ELECTRIC CURRENT THROUGH GASESBOOK - HC VERMA ENGLISHCHAPTER - ELECTRIC CURRENT THROUGH GASESEXERCISE - Short answer
6 Videos
Similar Questions
The potential energy U(x) of a particle moving along x - axis is given by U(x)=ax−bx2. Find the equilibrium position of particle.
View SolutionThe energy stored in coil carrying current I is U. If current is halved, then energy stored in the coil will be (a) U/2 (b) U/4 (c) 2U (d) 4U
View SolutionThe energy stored in coil carrying current I is U. If current is halved, then energy stored in the coil will be (a) U/2 (b) U/4 (c) 2U (d) 4U
View SolutionA nuclear reactor using .235U generates 250MW of electric power. The efficiency of the reactor (i.e., efficiency of conversion of thermal energy into electrical energy) is 25%. What is the amount of .235U used in the reactor per year? The thermal energy released per fission of .235U is 200MeV.
View SolutionA current i1=i0sinωt passes through a resistor of resistance R. How much thermal energy is produced in one time period? A current i2=−i0sinωt passes through the resistor. How much thermal energy is produced in one time period? If i1andi2 both pass through the resistor simultaneously, how much thermal energy is produced? Is the principle of superposition obeyed in this case?
View SolutionIn the given cirucit diagram the current through the 1ohm resistor is I. Find the value of 2I (in A)?
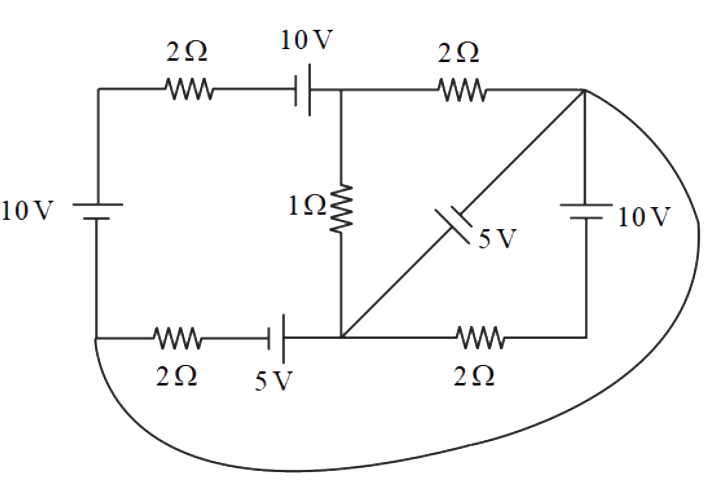
View SolutionA conductor is being charged by connecting it in series with a resistance and an ideal battery. The battery supplies energy at a rate u(t), the thermal energy of the resistor Increases at a rate Ur(t) and the capacitor stores energy at a rate Uc(t).What can be concluded about the relationship between UR(t) and U_(c)(t) at different stages of charging of condenser.
View SolutionLet gravitational potential energy U is given by U=A√xB+x2, where x is distance. The dimensional formula of A/B is
View SolutionA resistor develops 400J of thermal energy in 10 s when a current of 2A is pased through it. (a) Find its resistance . (b) If the current is increased to 4 A, what will be the energy developed in 10 s.
View SolutionFind the dimensional formulae of
a the charge Q.
the potential V,
c. the capacitance C and
d the resistance R.
Some of the equations containing these quantities are <br>Q=It, U=VIt, Q=CV and V=RI,
where I denotes the electric current, t is time and U is energy.
View Solution
