A 20(μ)Fcapacitor is joined to a battery of emf 6.0V through a resistance of 100(Ω).find the charge on the capacitor 2.0ms after the connections are made .
To solve the problem of finding the charge on a capacitor after a certain time when connected to a battery through a resistor, follow these steps:
Step 1: Identify the given values
- Capacitance, C=20μF=20×10−6F
- EMF of the battery, V=6.0V
- Resistance, R=100Ω
- Time, t=2.0ms=2.0×10−3s
Step 2: Calculate the time constant τ
The time constant τ for an RC circuit is given by the formula:
τ=R×C
Substituting the values:
τ=100Ω×20×10−6F=2×10−3s
Step 3: Use the formula for charge on the capacitor at time t
The charge Q on the capacitor at time t is given by the formula:
Q(t)=C⋅V⋅(1−e−tτ)
Substituting the known values:
Q(2ms)=20×10−6F⋅6.0V⋅(1−e−2×10−32×10−3)
Step 4: Simplify the exponent
Since 2×10−32×10−3=1:
Q(2ms)=20×10−6F⋅6.0V⋅(1−e−1)
Step 5: Calculate e−1
Using the approximate value of e−1:
e−1≈0.3679
Thus,
1−e−1≈1−0.3679=0.6321
Step 6: Calculate the charge Q
Now substituting this back into the equation:
Q(2ms)=20×10−6F⋅6.0V⋅0.6321
Calculating:
Q(2ms)=120×10−6⋅0.6321≈75.85×10−6C
or
Q(2ms)≈75.85μC
Final Answer
The charge on the capacitor 2.0 ms after the connections are made is approximately 75.85μC.
---
- Capacitance, C=20μF=20×10−6F
- EMF of the battery, V=6.0V
- Resistance, R=100Ω
- Time, t=2.0ms=2.0×10−3s
The time constant τ for an RC circuit is given by the formula:
τ=R×C
Substituting the values:
τ=100Ω×20×10−6F=2×10−3s
The charge Q on the capacitor at time t is given by the formula:
Q(t)=C⋅V⋅(1−e−tτ)
Substituting the known values:
Q(2ms)=20×10−6F⋅6.0V⋅(1−e−2×10−32×10−3)
Since 2×10−32×10−3=1:
Q(2ms)=20×10−6F⋅6.0V⋅(1−e−1)
Using the approximate value of e−1:
e−1≈0.3679
Thus,
1−e−1≈1−0.3679=0.6321
Now substituting this back into the equation:
Q(2ms)=20×10−6F⋅6.0V⋅0.6321
Calculating:
Q(2ms)=120×10−6⋅0.6321≈75.85×10−6C
or
Q(2ms)≈75.85μC
The charge on the capacitor 2.0 ms after the connections are made is approximately 75.85μC.
Topper's Solved these Questions
- BOOK - HC VERMA ENGLISHCHAPTER - ELECTRIC CURRENT IN CONDUCTORSEXERCISE - questions for short answer17videos
ELECTRIC CURRENT IN CONDUCTORS
- BOOK - HC VERMA ENGLISHCHAPTER - ELECTRIC CURRENT IN CONDUCTORSEXERCISE - objective 29videos
ELECTRIC CURRENT IN CONDUCTORS
- BOOK - HC VERMA ENGLISHCHAPTER - DISPERSION AND SPECTRAEXERCISE - Question for short Answer6videos
DISPERSION AND SPECTRA
- BOOK - HC VERMA ENGLISHCHAPTER - ELECTRIC CURRENT THROUGH GASESEXERCISE - Short answer6videos
ELECTRIC CURRENT THROUGH GASES
Similar Questions
A parallel-plalte capacitor has plate area 20cm2,plate separation 1.0mm and a dielectric slab of dielaectric constant 5.0 filling up the space between the plates.This capacitor is joined to a battery of emf 6.0V through a 100k(Ω)resistor.find the energy of the capacitor 8.9(μ)safter the connections are made.
View SolutionA capacitor of capacitance 8.0(μ)F is connected to a bettery of emf 6.0V through a resistance of 24(Ω).Find the current in the circuit (a)just after the connections are made and (b)one time constant after the connections are made.
View SolutionThe plates of a 50(μ)F capacitor charged to 400(μ)C are connected through a resistance of 1.0k(ohm). Find the charge remaining on the capacitor 1s after the connection is made.
View SolutionA parallel-plate capacitor of plate area 40cm2 and separation between the plates 0.10mm is connected to a battery of emf2.0V through a 16Ω resistor. Find the electric field in the capacitor 10ns after the connections are made.
View SolutionAn LR circuit with a battery connected at t =0. Which of the following quantities will be zero just after the connection?
View SolutionA capacitor of capacitance 12(μ)Fis connected to a battery of emf 6.00V and internal resistance 1.00(Ω)through resistanceless leads. 12.0(mu)s after the connections are made, what will be (a) the current in the circuit, (b)the power delivered by the battery ,(c)the power dissipated in heat and (d)the rate at which the energy stored in the capacitor is increasing.
View SolutionA capacitor of capacitance as C is given a charge Q. At t=0,it is connected to an ideal battery of emf (ε)through a resistance R. Find the charge on the capacitor at time t.
View SolutionA capacitor of capacitance as C is given a charge Q. At t=0,it is connected to an ideal battery of emf (ε)through a resistance R. Find the charge on the capacitor at time t.
View SolutionFind the charge on each of the capacitor 0.20ms after the switch S is closed in Figure.
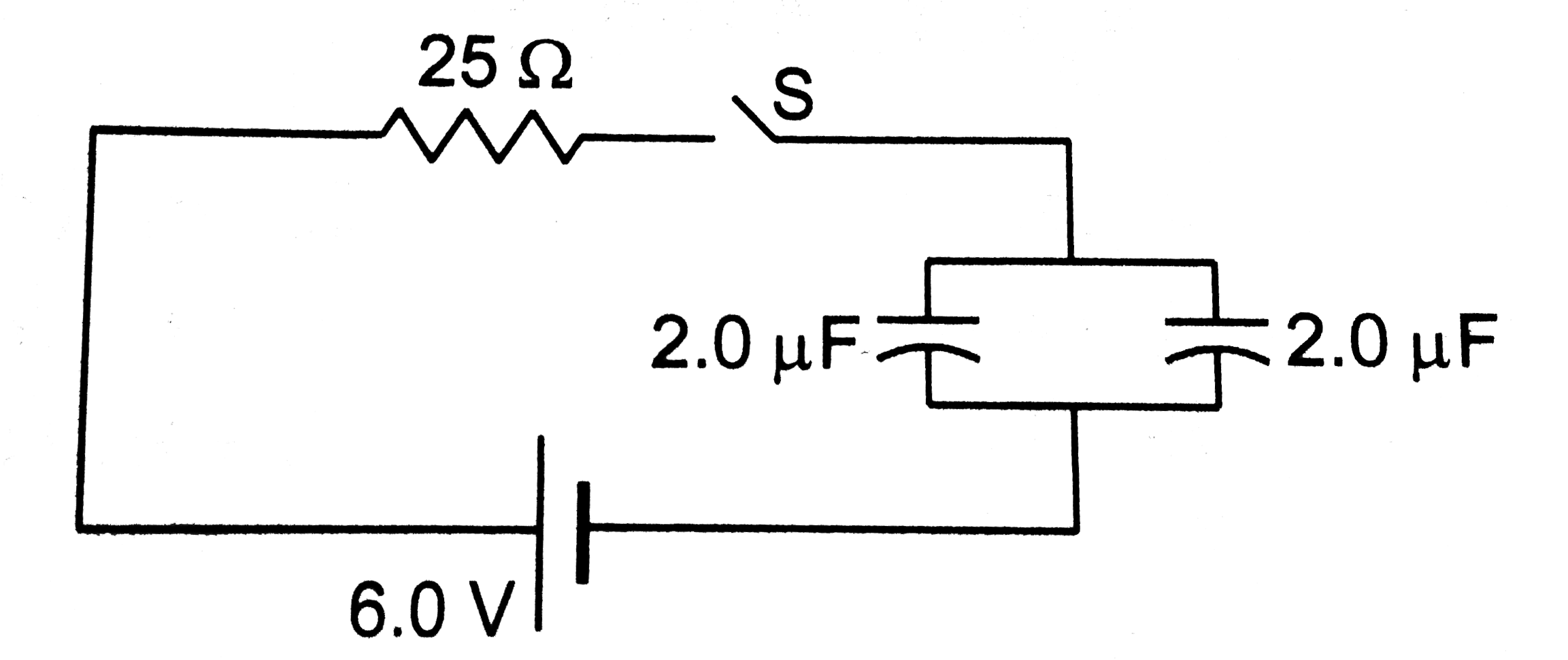 View Solution
View SolutionAn uncharged capacitor of capacitance 100μF is connected to a battery of emf 20V at t = 0 through a resistance 10Ω, then
(ii) time at which the rate has time miximum value isView Solution

