Prove that the force acting on a current carrying wire, joining two fixed points a and b in a uniform magnetic field, is independent of the shape of the wire.
To prove that the force acting on a current-carrying wire, joining two fixed points A and B in a uniform magnetic field, is independent of the shape of the wire, we can follow these steps:
Step 1: Understand the Force on a Current-Carrying Wire
The force F acting on a current-carrying wire in a magnetic field is given by the formula:
F=IL×B
where:
- I is the current flowing through the wire,
- L is the length vector of the wire in the direction of the current,
- B is the magnetic field vector.
Step 2: Define the Length Vector
The length vector L is defined as the vector that connects the two fixed points A and B. If we denote the distance between A and B as X, then:
L=X^n
where ^n is the unit vector in the direction from A to B.
Step 3: Calculate the Force
Substituting the expression for L into the force equation, we have:
F=I(X^n)×B
This simplifies to:
F=IX(^n×B)
The magnitude of the force can be expressed as:
F=IXBsin(θ)
where θ is the angle between the direction of the current (along ^n) and the magnetic field B.
Step 4: Independence from Shape
The key point here is that the length X and the angle θ are determined solely by the endpoints A and B and the orientation of the magnetic field. The shape of the wire does not affect the length X or the angle θ as long as the wire connects points A and B.
Thus, regardless of how the wire is shaped (whether it is straight, curved, or zigzagged), as long as it connects points A and B, the force F remains:
F=IXBsin(θ)
This shows that the force is independent of the shape of the wire.
Conclusion
Therefore, we have proven that the force acting on a current-carrying wire joining two fixed points A and B in a uniform magnetic field is independent of the shape of the wire.
---
The force F acting on a current-carrying wire in a magnetic field is given by the formula:
F=IL×B
where:
- I is the current flowing through the wire,
- L is the length vector of the wire in the direction of the current,
- B is the magnetic field vector.
The length vector L is defined as the vector that connects the two fixed points A and B. If we denote the distance between A and B as X, then:
L=X^n
where ^n is the unit vector in the direction from A to B.
Substituting the expression for L into the force equation, we have:
F=I(X^n)×B
This simplifies to:
F=IX(^n×B)
The magnitude of the force can be expressed as:
F=IXBsin(θ)
where θ is the angle between the direction of the current (along ^n) and the magnetic field B.
The key point here is that the length X and the angle θ are determined solely by the endpoints A and B and the orientation of the magnetic field. The shape of the wire does not affect the length X or the angle θ as long as the wire connects points A and B.
F=IXBsin(θ)
This shows that the force is independent of the shape of the wire.
Therefore, we have proven that the force acting on a current-carrying wire joining two fixed points A and B in a uniform magnetic field is independent of the shape of the wire.
Topper's Solved these Questions
- MAGNETIC FIELDBook:HC VERMA ENGLISHChapter:MAGNETIC FIELDExercise:QUESTIONS FOR SHORT ASNWER
Explore 10 Videos
- MAGNETIC FIELDBook:HC VERMA ENGLISHChapter:MAGNETIC FIELDExercise:objective2
Explore 9 Videos
- MAGNETIC FIELDBook:HC VERMA ENGLISHChapter:MAGNETIC FIELDExercise:objective 1
Explore 10 Videos
- LIGHT WAVESBook:HC VERMA ENGLISHChapter:LIGHT WAVESExercise:Question for short Answer
Explore 11 Videos
- MAGNETIC FIELD DUE TO CURRENTBook:HC VERMA ENGLISHChapter:MAGNETIC FIELD DUE TO CURRENTExercise:questions for short answer
Explore 12 Videos
Similar Questions
The force between two parallel current carrying wires is independent of
View Solutionthe force on current carrying wire placed in uniform magnetic field B as shown in figure is
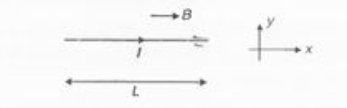
View SolutionCalculate the force on a current carrying wire in a uniform magnetic field as shown in Fig. 1.59.

View SolutionNo net force acts on a rectangular coil carrying a steady current when suspended freely in a uniform magnetic field.
View SolutionNo net force acts on a rectangular coil carrying a steady current when suspended freely in a uniform magnetic field.
View SolutionFind magnetic field at C by the system of current carrying wire.
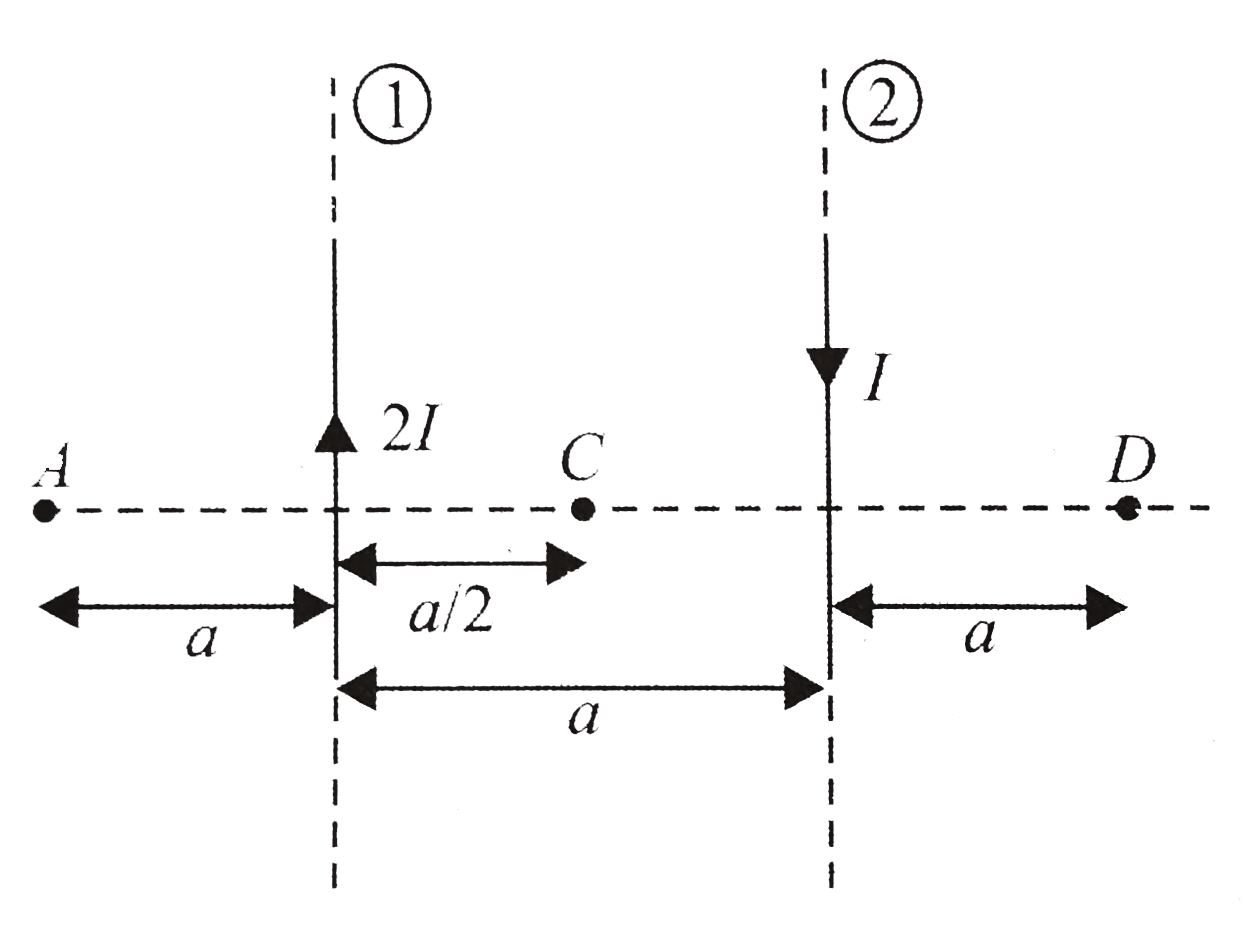

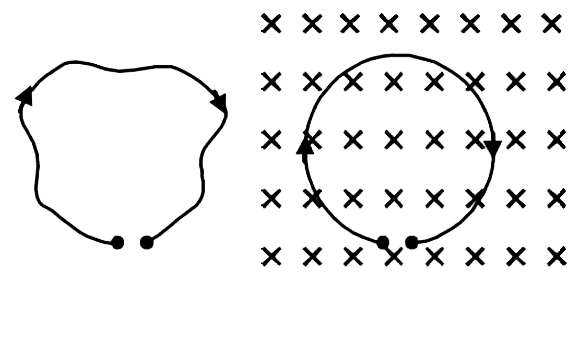
View SolutionA thin wire of length L is connected to two adjacent fixed points and carries a current I in the clockwise direction , as shown in the figure. When the system is put in a uniform magnetic field of strength B going into the plane of the paper , the wire takes the shape of a circle . The tension in the wire is
View SolutionA long current carrying wire is bent as shown. The magnetic field induction at O is

View SolutionA thin flexible wire of length L is connected to two adjacent fixed points and carries a current I in the clockwise direction, as shown in the figure. When the system is put in a uniform magnetic field of strength B going into the plane of the paper, the wire takes the shape of a circle. The tension in the wire is :

View SolutionA wire is bent in the form of a V shape and placed in a horizontal plane.There exists a uniform magnetic field B perpendicular to the plane of the wire. A uniform conducting rod starts sliding over the V shaped wire with a constant speed v as shown in the figure. If the wire no resistance, the current in rod wil
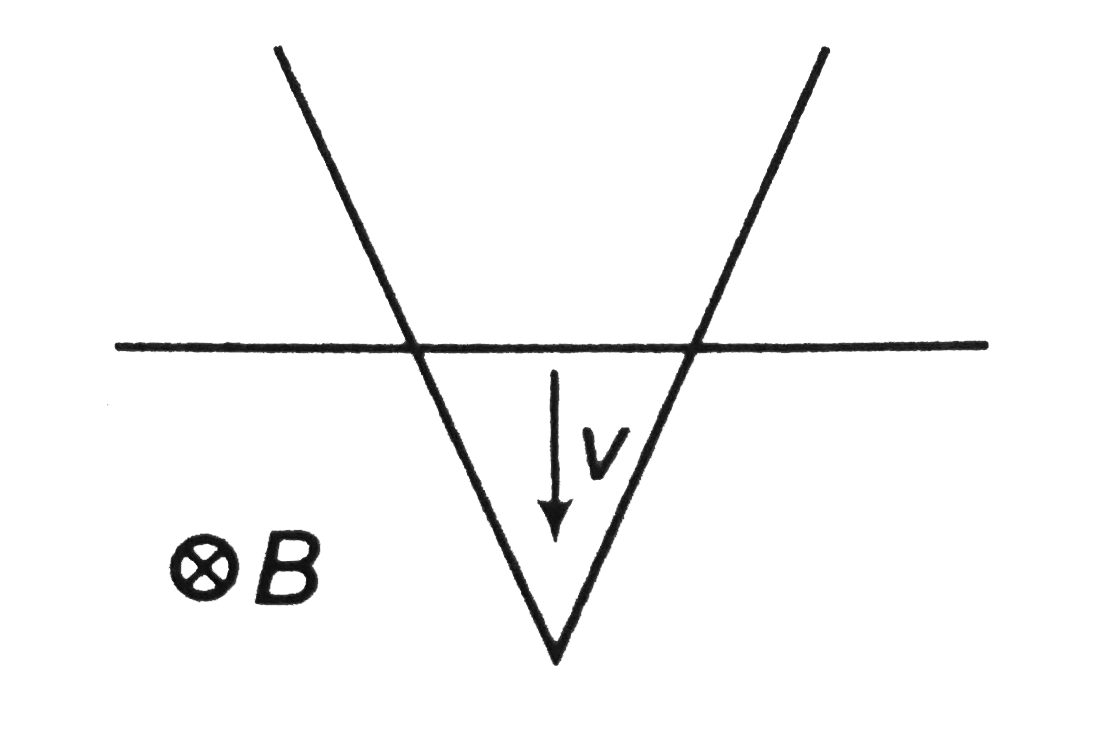
View Solution