A long , straight wire carries a current i. A particle having a positive charge q and mass m, kept at a distance x_0 from the wire is projected towards it with a speed v. Find the minimum separation between the wire and the particle.
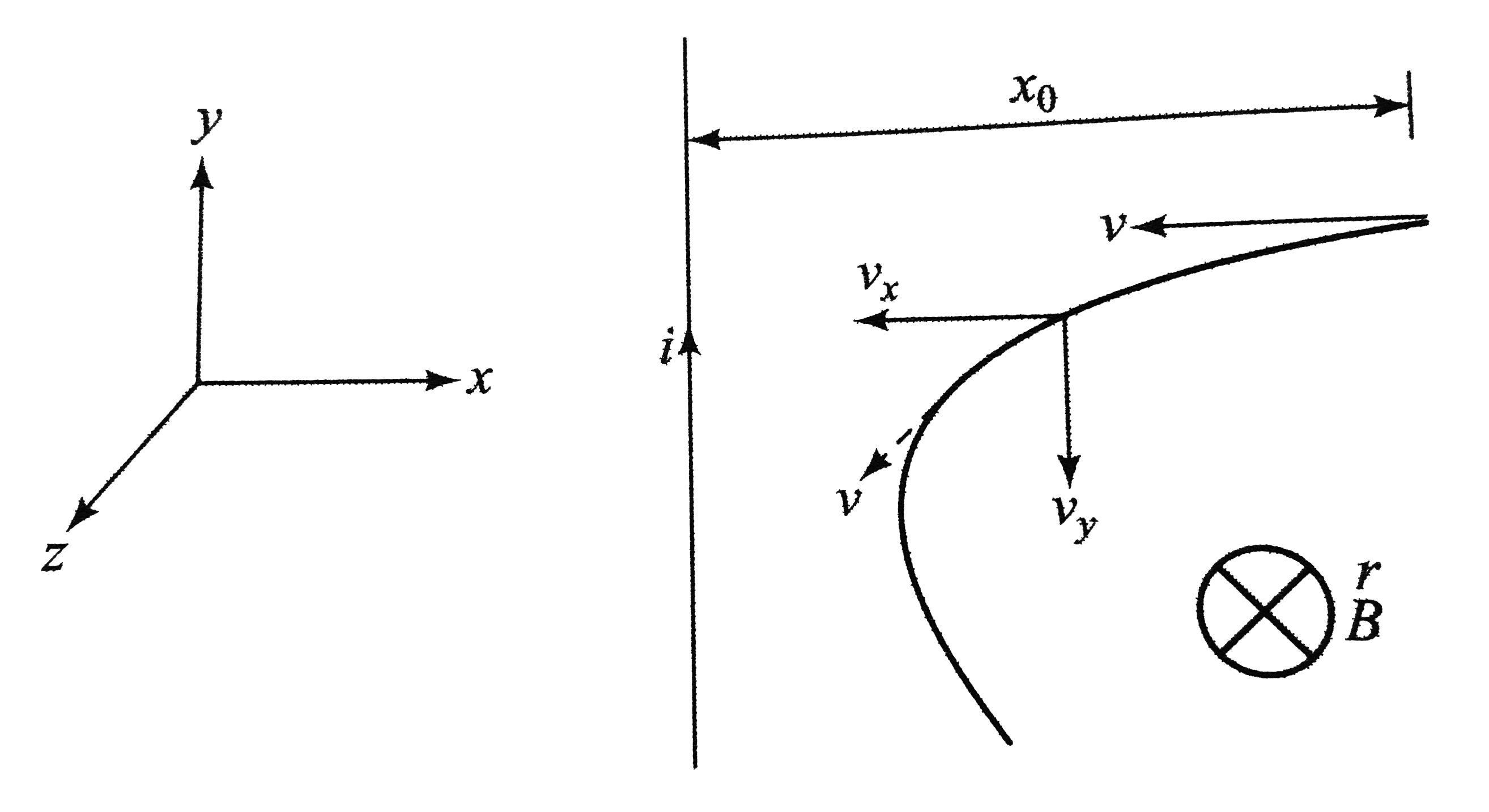
Solution: Let the particle be initially at P. Take
the wire as the y axis and the foot of perpendicular from
P to the wire as the origin. Take the line OP as the
x−aξs.Wehave,OP=x0.Themag≠ticfieldBatany<br>p∮→therightofthewireisalongthe¬ativez−aξs.<br>Themag≠ticforceonthepartic≤is,∴,∈the<br>x−ypla≠.Asthereisno∈itialvelocityalongthez−aξs,<br>themotionwillbe∈thex−ypla≠.Also,itsspeed<br>rema∈sunchan≥d.Asthemag≠ticfieldis¬<br>uniform,thepartic≤does¬goalonga∘≤.<br>Theforceattimetis( vec F)= (vec qv) xx (vec B)<br> = q((vec i)vx + (vec j)vy) xx (- (mu_0)i/2 pi x) vec k)<br> = ((vec j) q(v_x)) ((mu_0)i/2pi x) - (( vec i ) (qv_y)((mu_0)i/2 pi x)<br>Thusax=(Fxm)=−((μ0)qi2πm)(vyx)=−λ(Vyx).......(i)
whereλ=((μ0)qi2πm).
Also,ax=(dvxdt)=(dvxdx)(dxdt)=((vx)dvxdx)..........(ii)
As((vx)2)+((vy)2)=v2,
(2vx)(dvx)+((2vy)(dvy))=0
giv∈g((vx)(dvx))=−(vy)(dvy).....(iii)
From(i),(ii)and(iii),
((vy)dvydx)=λ(vy)x
or,dxx=(dvyλ).
Initiallyx=x0andvy=0.Atminiμmseparationom
thewire,vx=0sotˆvy=−v.
Thus(∫xx0)(dxx)=((∫0)−v)(dvyλ)
or,In(xx0)=(−vλ)
or, x = (x_0) (e^(-v/lambda))= (x_0) (e ^(- 2pi m v /((mu_0)qi))
Topper's Solved these Questions
- MAGNETIC FIELD DUE TO CURRENTBOOK - HC VERMA ENGLISHCHAPTER - MAGNETIC FIELD DUE TO CURRENTEXERCISE - Objective 1
12 Videos
- MAGNETIC FIELD DUE TO CURRENTBOOK - HC VERMA ENGLISHCHAPTER - MAGNETIC FIELD DUE TO CURRENTEXERCISE - Objective 2
7 Videos
- MAGNETIC FIELD DUE TO CURRENTBOOK - HC VERMA ENGLISHCHAPTER - MAGNETIC FIELD DUE TO CURRENTEXERCISE - questions for short answer
12 Videos
- MAGNETIC FIELDBOOK - HC VERMA ENGLISHCHAPTER - MAGNETIC FIELDEXERCISE - objective2
9 Videos
- MAGNETIC PROPERTIES OF MATTERBOOK - HC VERMA ENGLISHCHAPTER - MAGNETIC PROPERTIES OF MATTEREXERCISE - Short Answer
6 Videos
Similar Questions
A long straight wire carries a current i. A particle having a positive charge q and mass m, kept at distance x0 from the wire is projected towards it with speed v. Find the closest distance of approach of charged particle to the wire.

View SolutionA long straight wire carries a current i. A particle having a positive charge q and mass m, kept at distance x0 from the wire is projected towards it with speed v. Find the closest distance of approach of charged particle to the wire.


View Solution
Knowledge Check
A long straight wire carries a charge with linear density λ. A particle of mass m and a charge q is released at a distance r from the the wire. The speed of the particle as it crosses a point distance 2r is
A√qλlnrπm∈0B√qλln2πm∈0C√qλln22πm∈0D√qλln2πm∈0
A long straight wire carries a current I0=100amp , a particle having a positive charge q=100C and mass m=10gms is kept at a distance x0=10m from the axis of the wire is projected away from it with a speed v0=10m/sec. Find the maximum separation between particle and wire is found to be y×10m Find y.
View SolutionA positive point charge q of mass m, kept at a distance x0(in the same plane) from a fixed very long straight current is projected normally away from it with speed v.Find the maximum separation between the wire and the particle.
View SolutionA positive point charge q of mass m, kept at a distance x0(in the same plane) from a fixed very long straight current is projected normally away from it with speed v.Find the maximum separation between the wire and the particle.
View SolutionA long straight wire carries a charge with linear density λ. A particle of mass m and a charge q is released at a distance r from the the wire. The speed of the particle as it crosses a point distance 2r is
View Solutiona very long straight wire carries a current I. at the instant when are charge -Q at point P has velocity v as shown in figure the force on the charge is

View SolutionA straight wire carries a current of 10A. An electron moving at 103 m/s is at distance 2.0 cm from the wire. Find the force acting on the electron if its velocity is directed toward the wire?
View SolutionA straight wire carries a current of 10A. An electron moving at 103 m/s is at distance 2.0 cm from the wire. Find the force acting on the electron if its velocity is directed toward the wire?
View Solution
