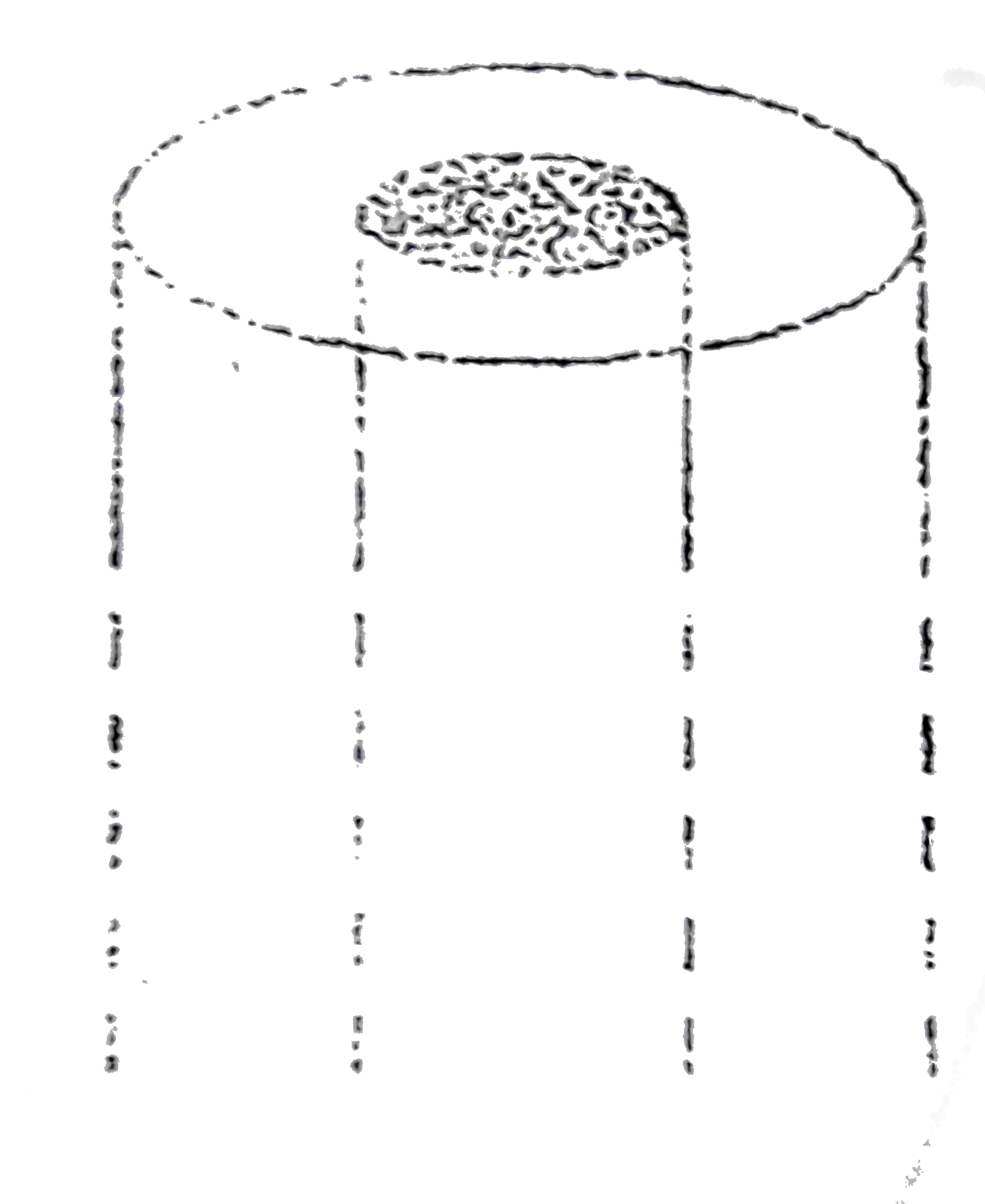
Consider a coaxial cable which consists of an inner wire of radius a surrounded by an outer shell of inner and outer radii b and c respectively. The inner wire carries an electric current (i_0) and the outer shell carries an equal current in opposite direction. Find the magnetic field at a distance x from the axis where (a) xlta, (b) altxltb, (c) bltxltc and (d)xgtc. Assume that the current density is uniform in the inner wire and also uniform in the outer shell.

Text Solution

Verified by Experts

Solution: A cross section of the cable is shown in figure.
Draw a circle of radius x with the centre at the axis of
the cable. The parts a,b,c and d of the figure
correspond to the four parts of the problem.By
symmetry, the magnetic field at each point of a circle
will have the same magnitude and will be tangential to
it. The circulation of B along this circle is, therefore,
$\oint (\to B) . \to d l = B 2 π x$
in each of the four parts of the figure.
$(a) T h e c u r r e n t e n c l o s e d w i t h \in t h e \circ \leq \in p a r t a i s$
$\frac{i_{0}}{{(π a)}^{2}} . π x^{2} = ((\frac{i_{0}}{a^{2}}) x^{2}) .$
$A m p e r e' s l a w \oint (\to B) . (\to d l) = (μ_{0}) i g i v e s$
$B 2 π x = ((m_{0}) (i_{0}) \frac{x^{3}}{a^{2}}) or B = (\frac{(μ_{0}) (i_{0}) x}{{(2 π a)}^{2}})$
The area of cross section of the outer shell is
$π c^{2} - π b^{2} . T h e a r e a o f c r o s s sec t i o n o f t h e o u t e r s h e l l$
$w i t h \in t h e \circ \leq \in p a r t c o f t h e f i g u r e i s (π x^{2} - π b^{2}) .$
$T h u s, t h e c u r r e n t t h r o u g h t h i s p a r t i s (\frac{i_{0} (x^{2} - b^{2})}{c^{2} - b^{2}}) . T h i s i s$
$\in t h e o p p o s i t e d i r e c t i o n \to t h e c u r r e n t (i_{0}) \in t h e \in \neq r$
$w i r e . T h u s, t h e \neq t c u r r e n t e n c l o s e d b y t h e \circ \leq i s$
$(i_{0}) - (\frac{i_{0} (x^{2} - b^{2})}{c^{2} - b^{2}}) = (\frac{i_{0} (c^{2} - x^{2})}{c^{2} - b^{2}})$ .
From Ampere's law,
$B 2 π x = ((μ_{0}) (i_{0}) \frac{c^{2} - x^{2}}{c^{2} - b^{2}})$
$or, B = ((μ_{0}) (i_{0}) \frac{c^{2} - x^{2}}{2 π x (c^{2} - b^{2})}) .$
$(d) T h e \neq t c u r r e n t e n c l o s e d b y t h e \circ \leq \in p a r t d o f$
the figure is zero and hence
$B 2 π x = 0 or, B = 0 .$

Updated on:21/07/2023