Figure shows a square loop of edge a made of a uniform wire. A current i enters the loop at the point A and leaves it at the point C. Find the magnetic field at the point P which is on the perpendicular bisector of AB at a distance a/4 from it.
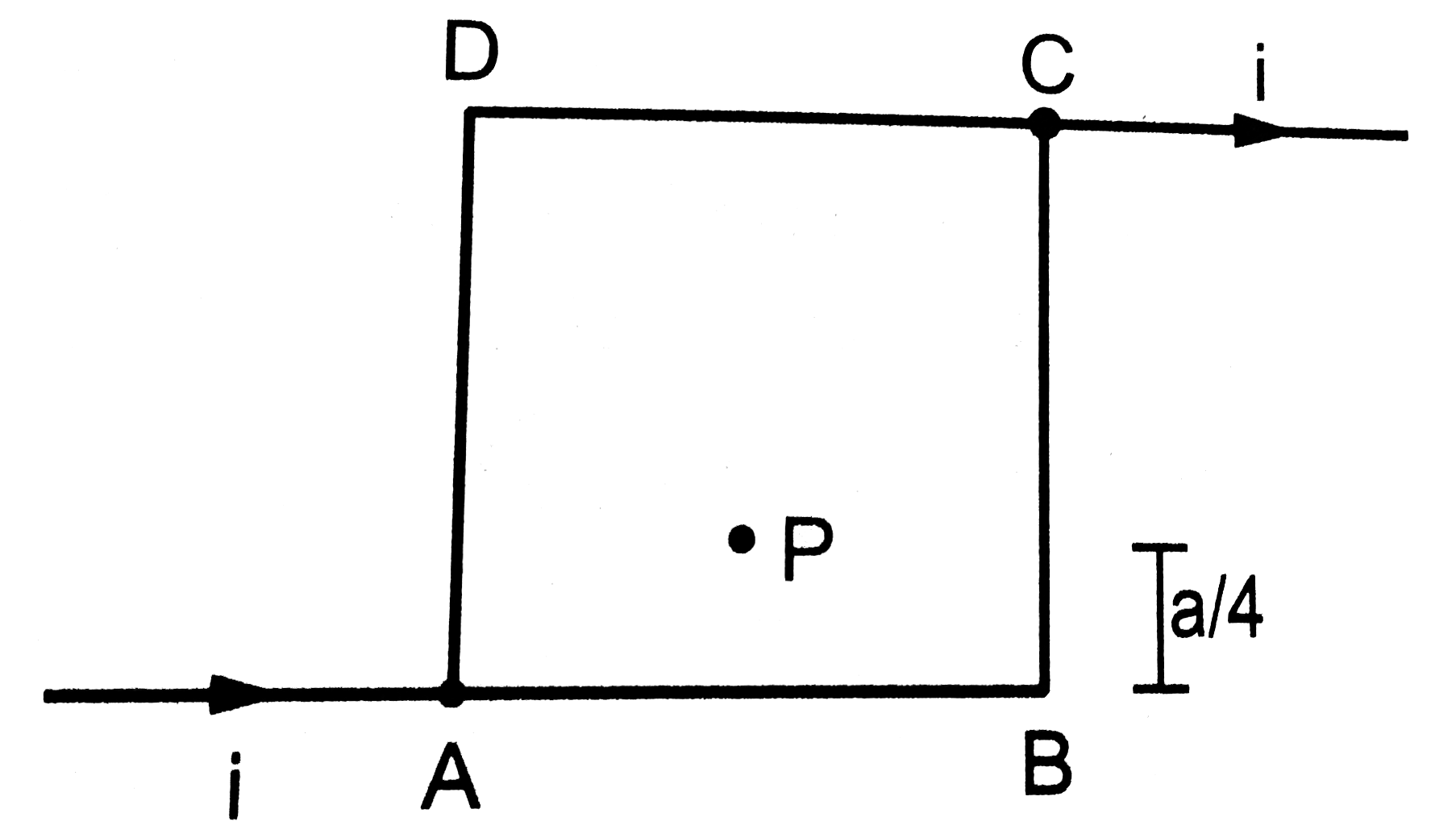
B at P due to AD =μo4π.i2.4a2.a⎡⎢
⎢
⎢
⎢⎣(a2)√(a2)2+(a4)2+(a2)√(a2)2+(3a4)2⎤⎥
⎥
⎥
⎥⎦along
=μoi2πa⎡⎢
⎢
⎢
⎢⎣(a2)√(a2)2+(a4)2+(a2)√(a2)2+(3a4)2⎤⎥
⎥
⎥
⎥⎦ along<br>BatPdue→AC=(mu_o)/(4pi).(i)/(2). (16)/(9a^2.a 2.[(((3a)/(4)))/(sqrt(((3a)/(4))^2 + ((a)/(2))^2))<br>(4mu_oi)/(9pia) [(((3a)/(4)))/(sqrt(((a)/(4))^2 +((3a)/(2))^2))]along<br>B at P due to AB = (mu_oi)/(4pi).(i)/(2) . (16)/(9a^2). a. 2 [(((a)/(4)))/sqrt(((a)/(4))^2 + ((a)/(2))^2 along<br>BatPdue→BC = (mu_o)/(4pi).(i)/(2). (4)/(a^2).a. [(((a)/(2)))/ sqrt(((a)/(2))^2 + ((a)/(2))^2) +(((a)/(2)))/sqrt(((a)/(2))^2 + ((3a)/(4))^2)] along<br>=(um_oi)/(2pia)[(((a)/(2)))/sqrt(((a)/(2))^2 +((a)/(2))^2) + (((a)/(2)))/(sqrt(((a)/(2))^2 +((3a)/(4))^2))]along⊗<br>so,net B=4μoiπa⎡⎢
⎢
⎢
⎢⎣(a4)√(a2)2+(a4)2⎤⎥
⎥
⎥
⎥⎦−4μoi9πa⎡⎢
⎢
⎢
⎢⎣(3a4)√(a2)2+(3a4)2⎤⎥
⎥
⎥
⎥⎦
=4μoiπa.14⎡⎢
⎢⎣1√14+116−4μoi9πa.34⎡⎢
⎢⎣1√14+916⎤⎥
⎥⎦
=4μoiπa[4√5]−μoi3πa[4√13][4√13]along
=4μoi2πa[1√5−13√13]along=2πoiπa[1√5−13√13]along.
Topper's Solved these Questions
- MAGNETIC FIELD DUE TO CURRENTBOOK - HC VERMA ENGLISHCHAPTER - MAGNETIC FIELD DUE TO CURRENTEXERCISE - questions for short answer
12 Videos
- MAGNETIC FIELD DUE TO CURRENTBOOK - HC VERMA ENGLISHCHAPTER - MAGNETIC FIELD DUE TO CURRENTEXERCISE - Objective 2
7 Videos
- MAGNETIC FIELDBOOK - HC VERMA ENGLISHCHAPTER - MAGNETIC FIELDEXERCISE - objective2
9 Videos
- MAGNETIC PROPERTIES OF MATTERBOOK - HC VERMA ENGLISHCHAPTER - MAGNETIC PROPERTIES OF MATTEREXERCISE - Short Answer
6 Videos
Similar Questions
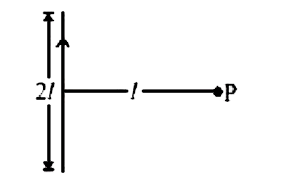
Find the magnetic field at a point P on the perpendicular bisector of the current carrying conductor :-
View SolutionConsider the situation described in the previous problem. Suppose the current I enters the loop at the point A and leaves it at the point B. Find the magnetic field at the centre of the loop.
View Solution
Knowledge Check
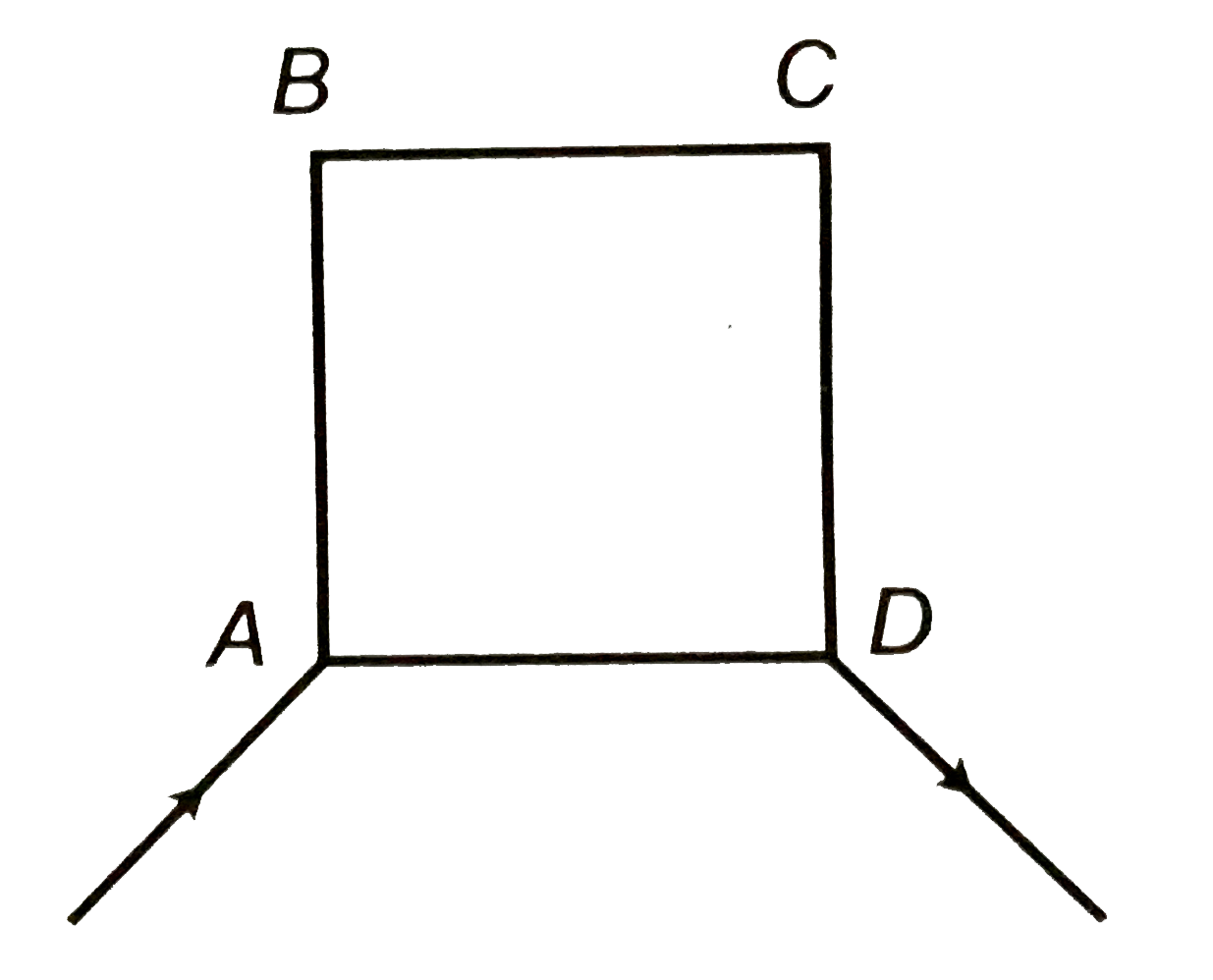
ABCD is a square loop made of a uniform conducting wire. A current enters the loop at A and leaves at D. The magnetic field is
 Azero only at the centre of the loopBmaximum at the centre of the loopCzero at all point outside the centre loopDzero at all points inside the loop
Azero only at the centre of the loopBmaximum at the centre of the loopCzero at all point outside the centre loopDzero at all points inside the loopPQRS is a square loop of a conducting wire. A current I enters the loop at Pand leaves the loop at S. The magnitude of magnetic field at the centre o of the square is
 Aμ04π2√2IaBμ04π4√2IaCμ04π4√2IaDzero
Aμ04π2√2IaBμ04π4√2IaCμ04π4√2IaDzero
Figure shows a square loop made from a uniform wire. If a battery is connected between the pionts A and C. What will be the magnetic field at the centre O of the square?
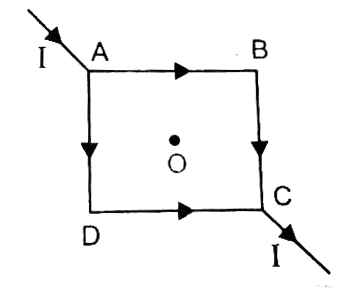
View SolutionFigure shows a square loop made from a uniform
wire. Find the magnetic field at the centre of the square
if a battery is connected between the points A and C.

View SolutionFigure shows a square loop made from a uniform
wire. Find the magnetic field at the centre of the square
if a battery is connected between the points A and C.

View SolutionIn the figure, the current l enters the circular loop of uniform wire of radius r at A and leaves it at B. The magnetic field of the centre of circular loop is

View SolutionIn the figure, the current l enters the circular loop of uniform wire of radius r at A and leaves it at B. The magnetic field of the centre of circular loop is

View SolutionFigure shows a square loop made from a uniform wire. Find the magnetic field at the centre of the square if a battary is connected between points A and C.

View Solution
