The magnetic field energy in an inductor changes from maximum value to minimum value in 5.0ms when connected to an AC source. The frequency of the source is
20 Hz
50 Hz
200Hz
500Hz.
The correct Answer is:B
To find the frequency of the AC source when the magnetic field energy in an inductor changes from maximum to minimum value in 5.0 ms, we can follow these steps:
Step 1: Understand the relationship between energy and current in an inductor
The energy stored in an inductor (E) is given by the formula:
E=12LI2
where L is the inductance and I is the current.
Step 2: Express current in terms of time
The current in an inductor connected to an AC source can be expressed as:
I(t)=Ipsin(ωt)
where Ip is the peak current and ω is the angular frequency.
Step 3: Determine the maximum and minimum energy states
The maximum energy occurs when sin2(ωt)=1 and the minimum energy occurs when sin2(ωt)=0. The transition from maximum to minimum energy occurs over a quarter of the AC cycle.
Step 4: Relate the time taken to the frequency
The time taken to go from maximum energy to minimum energy is:
Δt=T4
where T is the period of the AC signal. The period T is related to frequency f by:
T=1f
Thus,
Δt=14f
Step 5: Set up the equation with the given time
Given that Δt=5.0ms=5.0×10−3s, we can set up the equation:
5.0×10−3=14f
Step 6: Solve for frequency f
Rearranging the equation gives:
f=14×5.0×10−3=10.02=50Hz
Conclusion
The frequency of the AC source is 50Hz.
---
The energy stored in an inductor (E) is given by the formula:
E=12LI2
where L is the inductance and I is the current.
The current in an inductor connected to an AC source can be expressed as:
I(t)=Ipsin(ωt)
where Ip is the peak current and ω is the angular frequency.
The maximum energy occurs when sin2(ωt)=1 and the minimum energy occurs when sin2(ωt)=0. The transition from maximum to minimum energy occurs over a quarter of the AC cycle.
The time taken to go from maximum energy to minimum energy is:
Δt=T4
where T is the period of the AC signal. The period T is related to frequency f by:
T=1f
Thus,
Δt=14f
Given that Δt=5.0ms=5.0×10−3s, we can set up the equation:
5.0×10−3=14f
Rearranging the equation gives:
f=14×5.0×10−3=10.02=50Hz
The frequency of the AC source is 50Hz.
Topper's Solved these Questions
- ALTERNATING CURRENTBOOK - HC VERMA ENGLISHCHAPTER - ALTERNATING CURRENTEXERCISE - Objective 2
7 Videos
- ALTERNATING CURRENTBOOK - HC VERMA ENGLISHCHAPTER - ALTERNATING CURRENTEXERCISE - Exercise
19 Videos
- ALTERNATING CURRENTBOOK - HC VERMA ENGLISHCHAPTER - ALTERNATING CURRENTEXERCISE - Workder Examples
8 Videos
- BOHR'S MODEL AND PHYSICS OF THE ATOMBOOK - HC VERMA ENGLISHCHAPTER - BOHR'S MODEL AND PHYSICS OF THE ATOMEXERCISE - Short Answer
10 Videos
Similar Questions
A variable inductor inductor is connected to an AC source. When inductance increases, The reactance
View SolutionThe magnetic field at a point inside a 2.0 mH inductor coil becomes 0.80 of its maximum value in 20μs when the inductor is joined to a battery. Find the resistance of the circuit.
View Solution
Knowledge Check
An inductor of 30 mH is connected to a 220 V, 100 Hz ac source. The inductive reactance is
A10.58ΩB12.64ΩC18.85ΩD22.67Ω
The magnetic field at a point inside a 2.0 mH inductor coil becomes 0.80 of its maximum value in 20μs when the inductor is joined to a battery. Find the resistance of the circuit.
View SolutionA bulb and a conender are connected in series with an A.C source. On increasing the frequency of the source its brightness will
View SolutionAn ideal inductor of inductance 50μH is connected to an AC source of 220V, 50 Hz. Find the inductive reactance.
View SolutionWhen an a.c source is connected across a resistor
View SolutionAn inductor wire has some resistnce R when connected to dc. It is connected to an ac source. Now the impedance of the wire will be more than R. (ture/false)
View SolutionAnswer the following:
(a) What do you understand by 'sharpness of resonance' for a series LCR resonant circuit? How is it related with the quality factor 'Q' of the circuit? Using the graphs given in the diagram, explain the factors which affect it. For which graph is the resistance (R ) minimum?
(b) A 2μF capacitor, 100Ω resistor and 8H inductor are connected in series with an ac source. Find the frequency of the ac source for which the current drawn in the circuit is maximum.
If the peak value of emf of the source is 200 V, calculate the (i) maximum current, and (ii) inductive and capacitive reactance of the circuit at resonance.
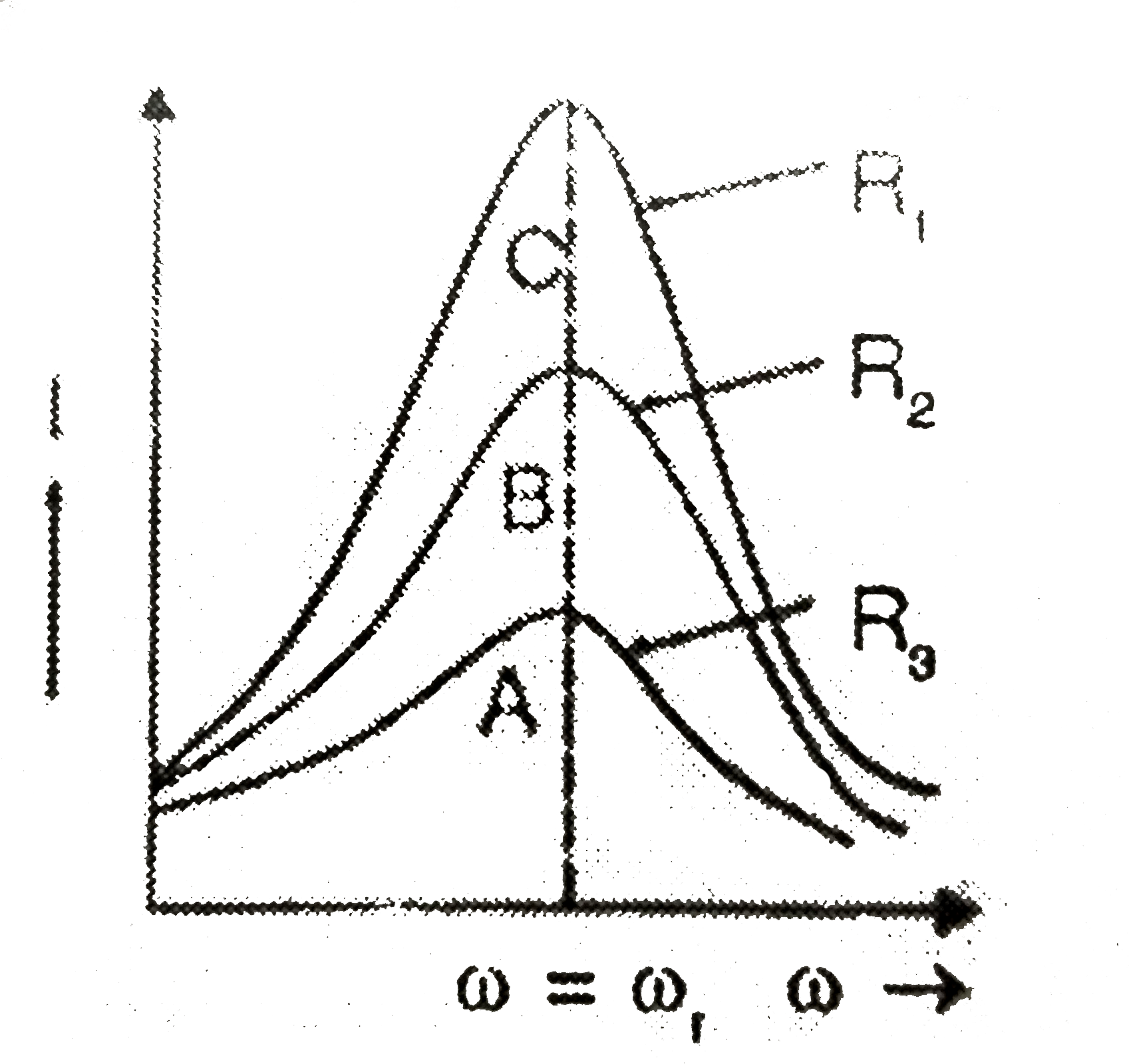
View SolutionAn inductor-coil , a capacitor and an AC source of rms voltage 24V are connected in series. When the frequency of the source is varied, a maximum rms current of 6.0A is observed. If this inductor coil is connected to a battery of emf12V and internal resistance 4.0Ω, what will be the current?
View Solution
