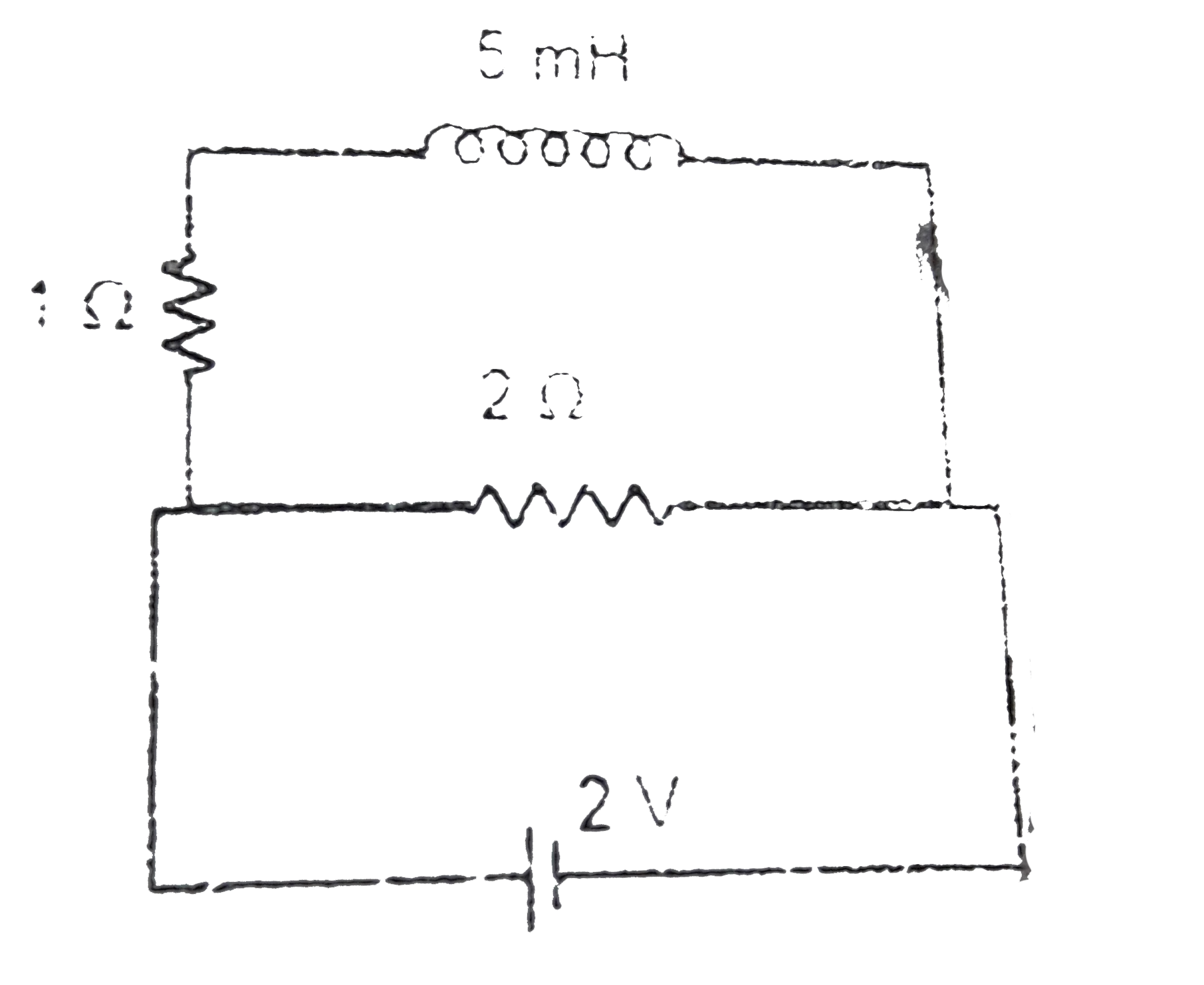
The magnetic field at a point inside a 2.0 mH inductor coil becomes 0.80 of its maximum value in 20μs when the inductor is joined to a battery. Find the resistance of the circuit.
To solve the problem step by step, we will use the relationship between the magnetic field in an inductor, the time constant, and the resistance of the circuit.
Step 1: Understand the given values
- Inductance L=2.0mH=2×10−3H
- Time interval t=20μs=20×10−6s
- The magnetic field reaches 0.8 of its maximum value.
Step 2: Write the expression for current in an inductor
The current I(t) in an inductor as it is connected to a battery is given by:
I(t)=I0(1−e−tτ)
where τ is the time constant defined as:
τ=LR
Step 3: Relate the magnetic field to the current
The magnetic field B inside the inductor can be expressed as:
B(t)=B0(1−e−tτ)
where B0 is the maximum magnetic field.
Step 4: Set up the equation using the given condition
At t=20μs, it is given that:
B(20μs)=0.8B0
Substituting this into the equation for B(t):
0.8B0=B0(1−e−20×10−6τ)
Dividing both sides by B0:
0.8=1−e−20×10−6τ
Step 5: Solve for the exponential term
Rearranging the equation gives:
e−20×10−6τ=1−0.8=0.2
Step 6: Take the natural logarithm of both sides
Taking the natural logarithm:
−20×10−6τ=ln(0.2)
This simplifies to:
20×10−6τ=−ln(0.2)
Step 7: Express τ in terms of L and R
Substituting τ=LR into the equation gives:
20×10−6RL=−ln(0.2)
Step 8: Rearranging to find R
Rearranging for R:
R=L⋅−ln(0.2)20×10−6
Step 9: Substitute the values
Substituting L=2×10−3H:
R=2×10−3⋅−ln(0.2)20×10−6
Step 10: Calculate R
Calculating −ln(0.2):
−ln(0.2)≈1.6094
Now substituting this value:
R=2×10−3⋅1.609420×10−6=3.2188×10−320×10−6=160.94Ω
Final Answer
The resistance of the circuit is approximately:
R≈160.9Ω
---
- Inductance L=2.0mH=2×10−3H
- Time interval t=20μs=20×10−6s
- The magnetic field reaches 0.8 of its maximum value.
The current I(t) in an inductor as it is connected to a battery is given by:
I(t)=I0(1−e−tτ)
where τ is the time constant defined as:
τ=LR
The magnetic field B inside the inductor can be expressed as:
B(t)=B0(1−e−tτ)
where B0 is the maximum magnetic field.
At t=20μs, it is given that:
B(20μs)=0.8B0
Substituting this into the equation for B(t):
0.8B0=B0(1−e−20×10−6τ)
Dividing both sides by B0:
0.8=1−e−20×10−6τ
Rearranging the equation gives:
e−20×10−6τ=1−0.8=0.2
Taking the natural logarithm:
−20×10−6τ=ln(0.2)
This simplifies to:
20×10−6τ=−ln(0.2)
Substituting τ=LR into the equation gives:
20×10−6RL=−ln(0.2)
Rearranging for R:
R=L⋅−ln(0.2)20×10−6
Substituting L=2×10−3H:
R=2×10−3⋅−ln(0.2)20×10−6
Calculating −ln(0.2):
−ln(0.2)≈1.6094
Now substituting this value:
R=2×10−3⋅1.609420×10−6=3.2188×10−320×10−6=160.94Ω
The resistance of the circuit is approximately:
R≈160.9Ω
Topper's Solved these Questions
- BOOK - HC VERMA ENGLISHCHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - Questions for short answer9videos
ELECTROMAGNETIC INDUCTION
- BOOK - HC VERMA ENGLISHCHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - Objective 210videos
ELECTROMAGNETIC INDUCTION
- BOOK - HC VERMA ENGLISHCHAPTER - ELECTRIC FIELD AND POTENTIALEXERCISE - Objective 27videos
ELECTRIC FIELD AND POTENTIAL
- BOOK - HC VERMA ENGLISHCHAPTER - ELECTROMAGNETIC WAVESEXERCISE - Exercise8videos
ELECTROMAGNETIC WAVES
Similar Questions
Knowledge Check
- Question 1 - Select One
An LC circuit contains a 20 mH inductor and a 50μF capacitor with an initial charge of 10 mC. The resistance of the circuit is negligible. Let the instant at which the circuit which is closed be t=0. At what time the energy stored is completely magnetic ?
At = 0Bt=1.54msCt=3.14msDt=6.28ms
The magnetic field energy in an inductor changes from maximum value to minimum value in 5.0ms when connected to an AC source. The frequency of the source is
View SolutionAn inductor coil stores 16 joules of energy and dissipates energy as heat at the rate of 320W when a current of 2 Amp is passed through it. When the coil is joined across a battery of emf 20V and internal resistance 20Ω the time constant for the circuit is τ. Find 100τ ( in seconds).
View SolutionA capacitor is connected across an inductor. At time t = 0 charge on the capacitor is equal to 1√2qmax, where qmax is the maximum charge on the capacitor. The time t, at which the energy stored in the capacitor is equal to the energy stored in the inductor is (The inductance of the inductor is L and capacitance of the capacitor is C. Resistance of the circuit is zero)
View SolutionAn average emf of 20 V is induced in an inductor when the current in it is changed from 2.5A in one direction to the same valute in the opposite direction in 0.1 s. Find the self inductance of the inductor.
View SolutionThe potential difference across a 150mH inductor as a function of time is shown in figure. Assume that the initial value of the current in the inductor is zero. What is the current when t=2.0ms? and t=4.0ms ?
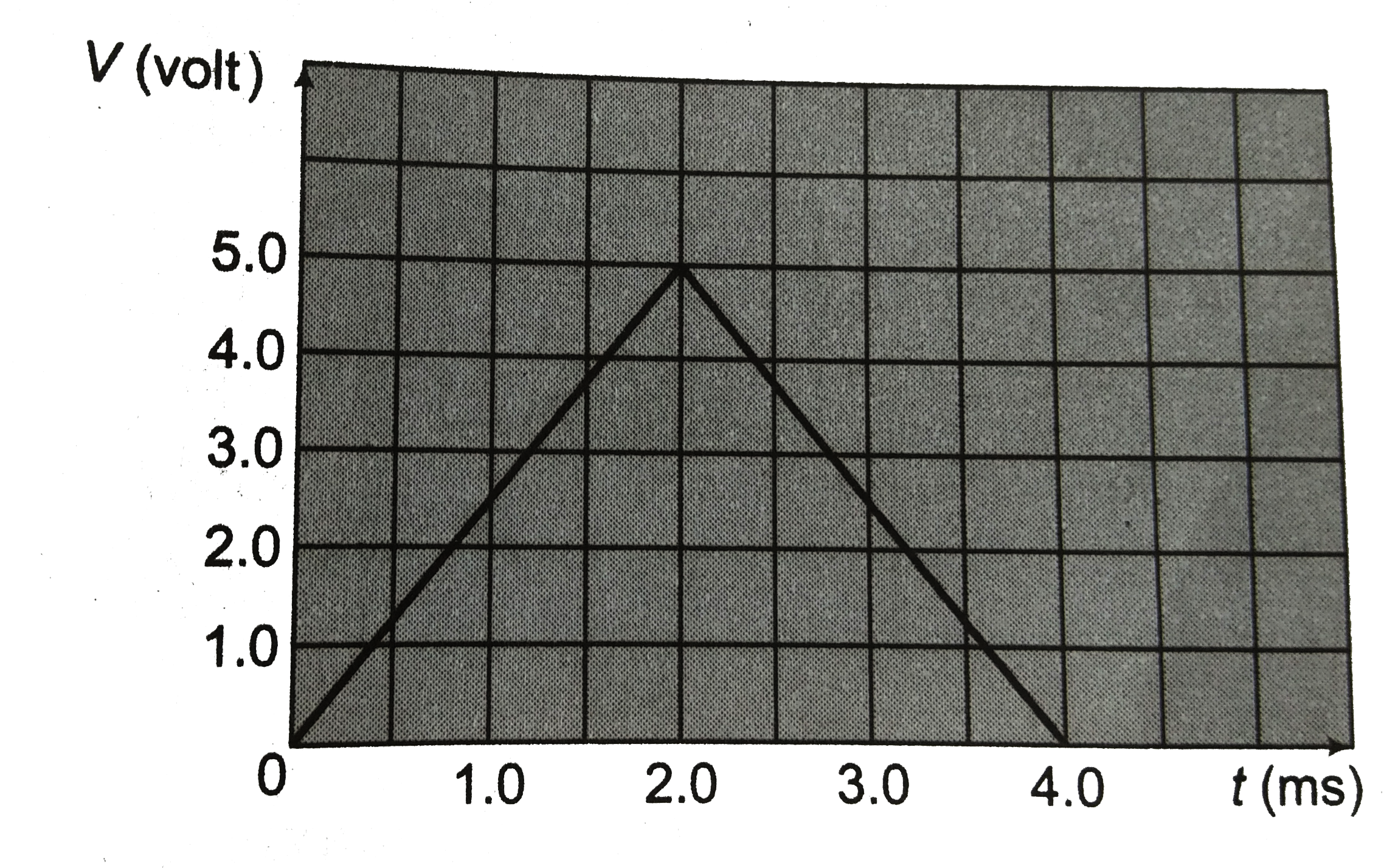 View Solution
View SolutionAn inductor coil stores 32 J of magnetic field energy and dissiopates energy as heat at the rate of 320 W when a current of 4 A is passed through it. Find the time constant of the circuit when this coil is joined across on ideal battery.
View SolutionAn inductor-coil , a capacitor and an AC source of rms voltage 24V are connected in series. When the frequency of the source is varied, a maximum rms current of 6.0A is observed. If this inductor coil is connected to a battery of emf12V and internal resistance 4.0Ω, what will be the current?
View Solution