An electric field (vec E) and a magnetic field (vec B)exist in a region . The fields are not perpendicular to each other.
This is not possible
No electromagnetic wave is passing through the region.
An electromagnetic wave may be passing through the region
An electromagnetic wave is certainly passing through the region.
The correct Answer is:C
Step by step video & image solution for An electric field (vec E) and a magnetic field (vec B)exist in a region . The fields are not perpendicular to each other. by Physics experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Topper's Solved these Questions
- ELECTROMAGNETIC WAVESBOOK - HC VERMA ENGLISHCHAPTER - ELECTROMAGNETIC WAVESEXERCISE - objective 2
5 Videos
- ELECTROMAGNETIC WAVESBOOK - HC VERMA ENGLISHCHAPTER - ELECTROMAGNETIC WAVESEXERCISE - Question for short answers
7 Videos
- ELECTROMAGNETIC WAVESBOOK - HC VERMA ENGLISHCHAPTER - ELECTROMAGNETIC WAVESEXERCISE - Worked Out Examples
5 Videos
- ELECTROMAGNETIC INDUCTIONBOOK - HC VERMA ENGLISHCHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - Questions for short answer
9 Videos
- GAUSS LAWBOOK - HC VERMA ENGLISHCHAPTER - GAUSS LAWEXERCISE - Short Question
7 Videos
Similar Questions
In a certain region of space electric field E and magnetic field B are perpendicular to each other and an electron enters region perpendicular to the direction of B and E both and moves undeflected, then velocity of electron is
(a) |E||B| (b) E×B (c) |B||E| (d) E.B
View SolutionIn a certain region of space electric field →E and magnetic field →B are perpendicular to each other and an electron enters in region perpendicular to the direction of →B and →E both and move underflected, then velocity of electron is
View Solution
Knowledge Check
Assertion : Electromagnetic waves are transverse in nature
Reason : The electric and magnetic fields in electromagnetic waves are perpendicular to each other and to the direction of propagation.AIf both assertion and reason are true and reason is the correct explanation of assertionBIf both assertion and reason are true but reason is not the correct explanation of assertionCIf assertion is true but reason is falseDIf both assertion and reason are false
The path of a charged particle in a uniform magnetic field, when the velocity and the magnetic field are perpendicular to each other is a
View SolutionAn electron enters a region where magnetic field (B) and electric field (E ) are mutually perpendicular, then
View Solution(A) : In electromagnetic waves electric field and magnetic field lines are perpendicular to each other. (R) : Electric field and magnetic field are self sustaining.
View SolutionIn a region, steady and uniform electric and magnetic fields are present . These two fields are parallel to each other. A charged particle is released from rest in this region . The path of the particle will be a
View SolutionAn uniform electric field of strength E exists in a region. An electron of mass m enters a point A perpendicular to x - axis with velocity V. It moves through the electric field and exists at point B. The components of velocity at B are shown in (Fig. 3.156). At B the y - component of velocity remain uncharged.
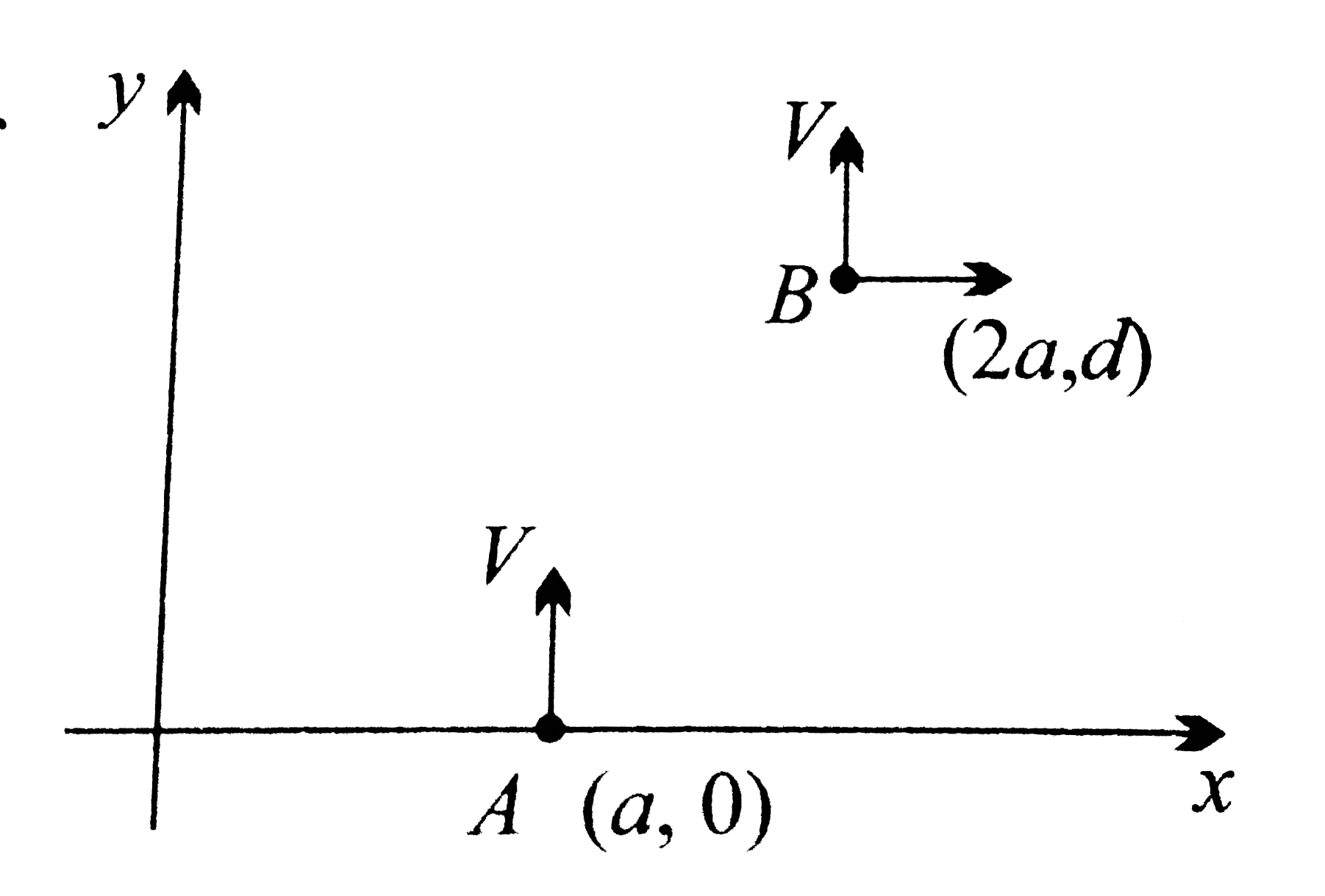 .
.
Find electric field.
View SolutionAn uniform electric field of strength E exists in a region. An electron of mass m enters a point A perpendicular to x - axis with velocity V. It moves through the electric field and exists at point B. The components of velocity at B are shown in (Fig. 3.156). At B the y - component of velocity remain uncharged.
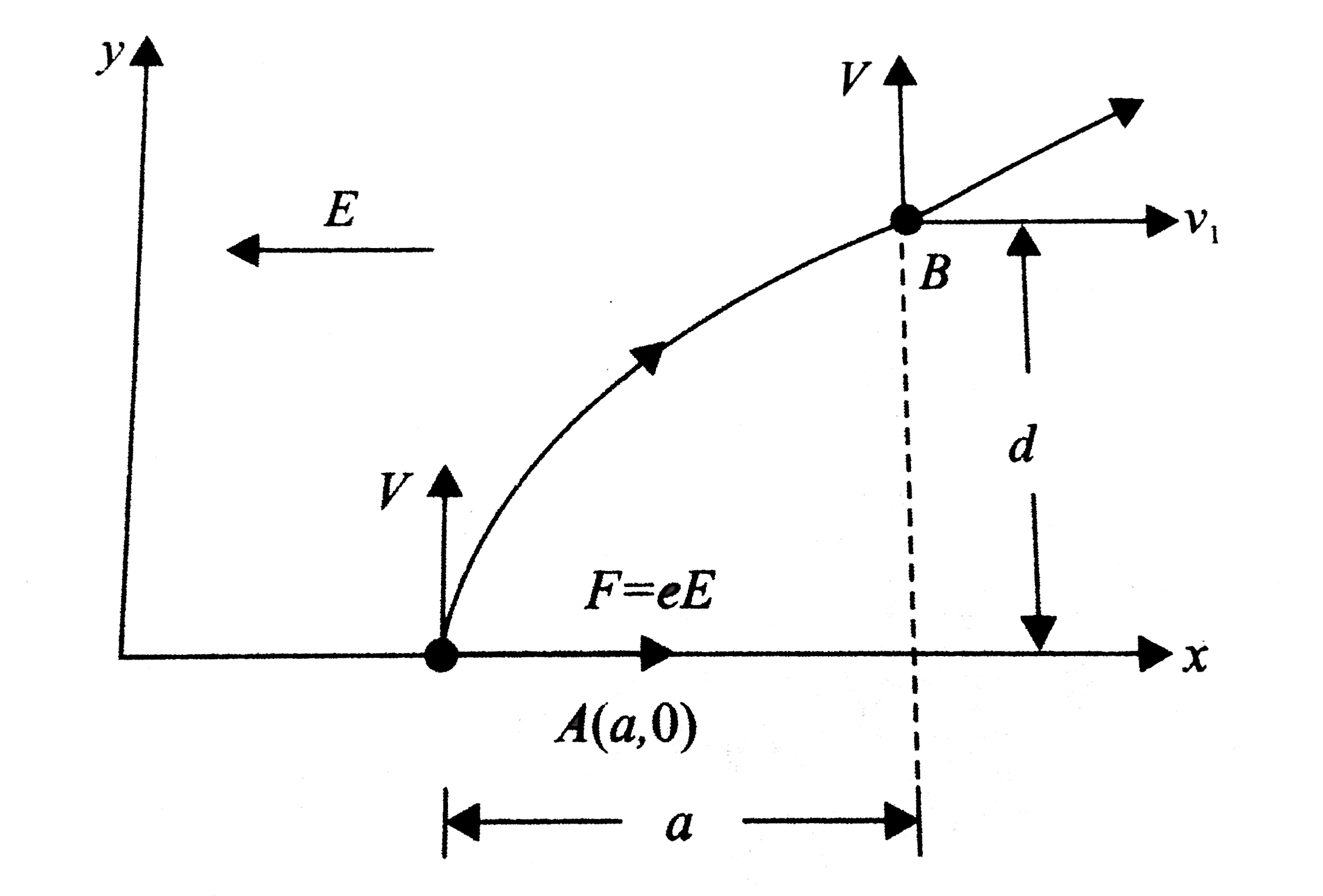 .
.
Find velocity at B.
View SolutionA particle having a mass of 10−2kg carries a charge of 5×10−8C. The particle is given an initial horizontal velocity of 105msec−1 in the presence of electric field →E and magnetic field →B. To keep the particle moving in a horizontal direction, it is necessary that
A. →B should be perpendicular to the direction of velocity and →E should be along the direction of velocity
B. Both →B and →E should be along the direction of velocity
C. Both →B and →E are mutually perpendicular and perpendicular to the direction of velocity
D. →B should be along the direction of velocity and →E should be perpendicular to the direction of velocity
View Solution
