A beam of 450 nm light is incident on a metal having work function 2.0 eV and placed in a magnetic field B. The most energetic electrons emitted perpendicular to the field are bent in circular arcs of radius 20 cm. Find the value of B.
To solve the problem, we will follow a step-by-step approach:
Step 1: Calculate the Energy of the Incident Photons
The energy of the incident photons can be calculated using the formula:
E=hcλ
Where:
- h (Planck's constant) = 4.14×10−15eV s
- c (speed of light) = 3×108m/s
- λ = 450 nm = 450×10−9m
Substituting the values:
E=(4.14×10−15eV s)(3×108m/s)450×10−9m
E=1.242×10−6eV m450×10−9m
E=2.76eV
Step 2: Calculate the Kinetic Energy of the Emitted Electrons
The kinetic energy (K.E) of the emitted electrons can be calculated using the work function (ϕ):
K.E=E−ϕ
Where ϕ=2.0eV:
K.E=2.76eV−2.0eV=0.76eV
Step 3: Convert Kinetic Energy to Joules
To convert the kinetic energy from electron volts to joules:
K.E=0.76eV×1.6×10−19J/eV=1.216×10−19J
Step 4: Calculate the Momentum of the Electrons
The momentum (p) of the electrons can be calculated using:
p=√2mK.E
Where m (mass of an electron) = 9.1×10−31kg:
p=√2×(9.1×10−31kg)×(1.216×10−19J)
p=√2.21×10−49
p≈4.67×10−25kg m/s
Step 5: Relate the Radius of the Circular Path to the Magnetic Field
The radius r of the circular path of the electrons in a magnetic field is given by:
r=mvqB
Where:
- q (charge of an electron) = 1.6×10−19C
- Rearranging gives us:
B=mvqr
Step 6: Substitute Values to Find the Magnetic Field
We know r=0.20m:
B=(9.1×10−31kg)×(v)(1.6×10−19C)×(0.20m)
We need to express v in terms of momentum:
p=mv⇒v=pm
Substituting p:
B=pq⋅r
B=4.67×10−25kg m/s(1.6×10−19C)⋅(0.20m)
B=4.67×10−253.2×10−20
B≈1.46×10−5T
Final Answer
The value of the magnetic field B is approximately:
B≈1.46×10−5T
The energy of the incident photons can be calculated using the formula:
E=hcλ
Where:
- h (Planck's constant) = 4.14×10−15eV s
- c (speed of light) = 3×108m/s
- λ = 450 nm = 450×10−9m
E=(4.14×10−15eV s)(3×108m/s)450×10−9m
E=1.242×10−6eV m450×10−9m
E=2.76eV
The kinetic energy (K.E) of the emitted electrons can be calculated using the work function (ϕ):
K.E=E−ϕ
Where ϕ=2.0eV:
K.E=2.76eV−2.0eV=0.76eV
To convert the kinetic energy from electron volts to joules:
K.E=0.76eV×1.6×10−19J/eV=1.216×10−19J
The momentum (p) of the electrons can be calculated using:
p=√2mK.E
Where m (mass of an electron) = 9.1×10−31kg:
p=√2×(9.1×10−31kg)×(1.216×10−19J)
p=√2.21×10−49
p≈4.67×10−25kg m/s
The radius r of the circular path of the electrons in a magnetic field is given by:
r=mvqB
Where:
- q (charge of an electron) = 1.6×10−19C
- Rearranging gives us:
B=mvqr
We know r=0.20m:
B=(9.1×10−31kg)×(v)(1.6×10−19C)×(0.20m)
p=mv⇒v=pm
Substituting p:
B=pq⋅r
B=4.67×10−25kg m/s(1.6×10−19C)⋅(0.20m)
B=4.67×10−253.2×10−20
B≈1.46×10−5T
The value of the magnetic field B is approximately:
B≈1.46×10−5T
Topper's Solved these Questions
- PHOTO ELECTRIC EFFECT AND WAVE PARTICLE DUALITYBOOK - HC VERMA ENGLISHCHAPTER - PHOTO ELECTRIC EFFECT AND WAVE PARTICLE DUALITYEXERCISE - objective I
14 Videos
- PHOTO ELECTRIC EFFECT AND WAVE PARTICLE DUALITYBOOK - HC VERMA ENGLISHCHAPTER - PHOTO ELECTRIC EFFECT AND WAVE PARTICLE DUALITYEXERCISE - objective II
7 Videos
- PHOTO ELECTRIC EFFECT AND WAVE PARTICLE DUALITYBOOK - HC VERMA ENGLISHCHAPTER - PHOTO ELECTRIC EFFECT AND WAVE PARTICLE DUALITYEXERCISE - question for short answer
13 Videos
- PERMANENT MAGNETSBOOK - HC VERMA ENGLISHCHAPTER - PERMANENT MAGNETSEXERCISE - Short Answer
11 Videos
- PHOTOMETRYBOOK - HC VERMA ENGLISHCHAPTER - PHOTOMETRYEXERCISE - All Questions
38 Videos
Similar Questions
Knowledge Check
A photon of energy E ejects a photoelectron from a metel surface whose work function is ϕ0. If this electron enters into a unifrom magnetic field of induction B in a direction perpendicular to the field and describes a circular path of radius r, then the radius r, is given by, (in the usual notation)
A√2m(E−ϕ0)eBB√(2m(E−ϕ0))eBC√2m(E−ϕ0)mBD√2m(E−ϕ0)eB
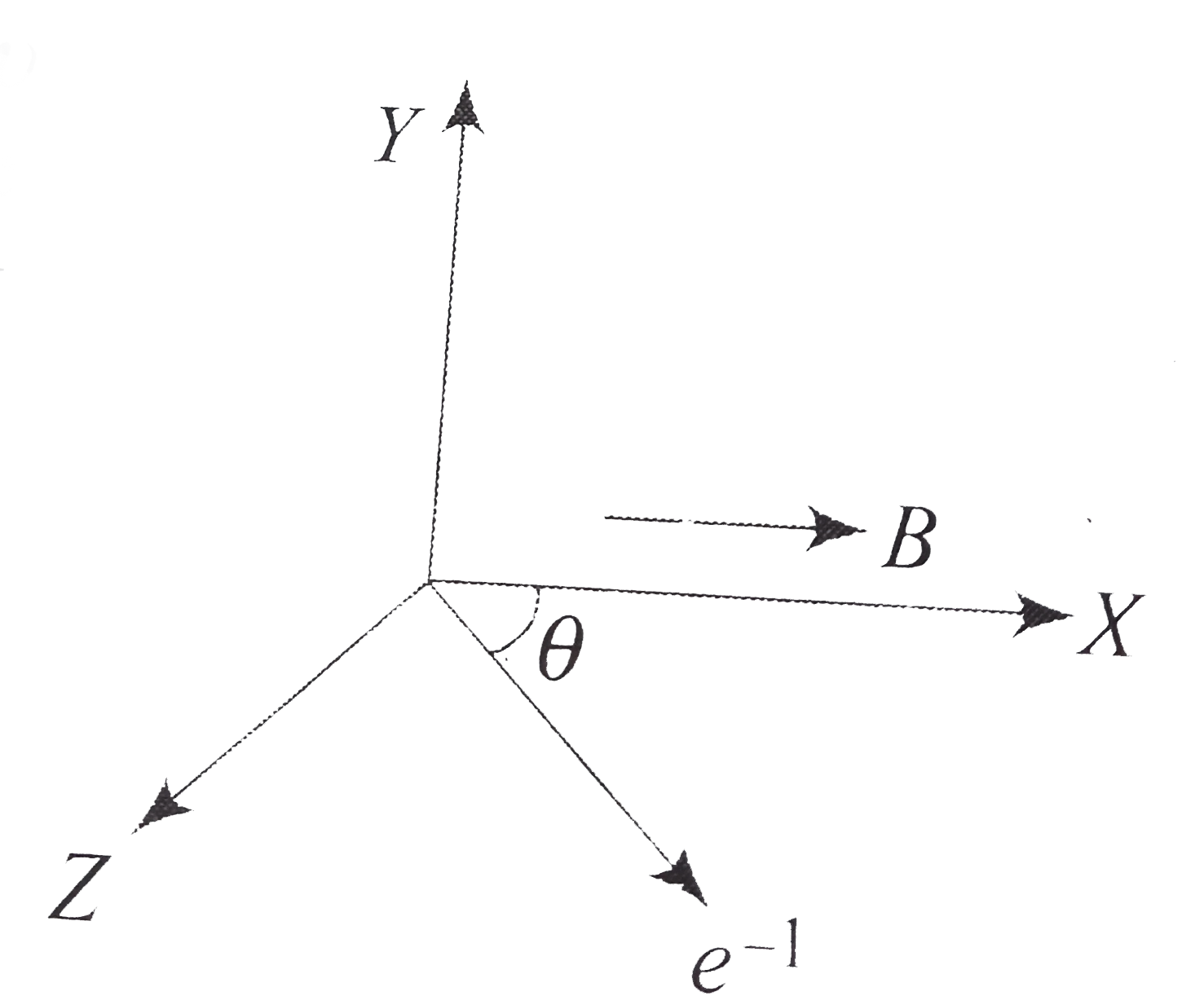
Light having photon energy hυ is incident on a metallic plate having work function ϕ to eject the electrons. The most energetic enectrons are then allowed to enter in a region of uniform magnetic field B as shown in Fig. The electrons are projected In X-Z plane making an angle θ with X-axis and magnetic field is →B=B0ˆi along X-axis maximum pitch of the helix described by an electron is found to be p. Take mass of electron as m and charge as q. Based on the above information, answer the following questions:
Q. The plot between X-coordinate of the location of electron as a function of time for different frequencies υ of the incident light is
View Solution
Light having photon energy hυ is incident on a metallic plate having work function ϕ to eject the electrons. The most energetic enectrons are then allowed to enter in a region of uniform magnetic field B as shown in Fig. The electrons are projected In X-Z plane making an angle θ with X-axis and magnetic field is →B=B0ˆi along X-axis maximum pitch of the helix described by an electron is found to be p. Take mass of electron as m and charge as q. Based on the above information, answer the following questions:
Q. Considering the instant of crossing origin at t=0 ,the Z-coordinate of the location of electron as a function of time is
View Solution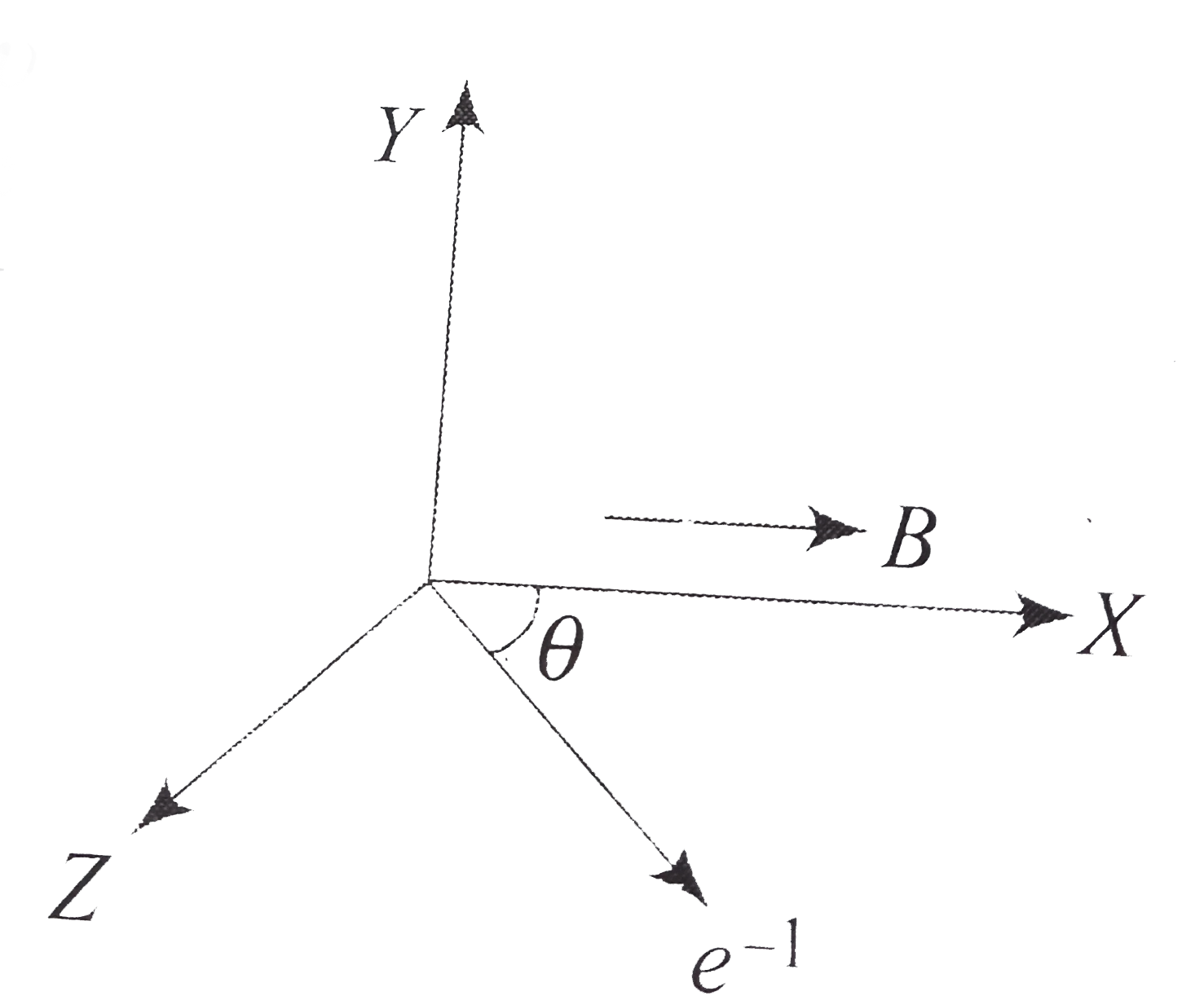
Light having photon energy hυ is incident on a metallic plate having work function ϕ to eject the electrons. The most energetic enectrons are then allowed to enter in a region of uniform magnetic field B as shown in Fig. The electrons are projected In X-Z plane making an angle θ with X-axis and magnetic field is →B=B0ˆi along X-axis maximum pitch of the helix described by an electron is found to be p. Take mass of electron as m and charge as q. Based on the above information, answer the following questions:
Q. The correct relation between p and B0 is
View SolutionIn the figure shown a semicircular wire loop is placed in a uniform magnetic field B=1.0T. The plane of the loop is perpendicular to the magnetic field. Current i=2A flows in the loop in the directions shown. Find the magnitude of the magnetic force in both the cases a and b. The radius of the loop is 1.0 m

View SolutionIn the figure shown a semicircular wire loop is placed in a uniform magnetic field B=1.0T. The plane of the loop is perpendicular to the magnetic field. Current i=2A flows in the loop in the directions shown. Find the magnitude of the magnetic force in both the cases a and b. The radius of the loop is 1.0 m

View SolutionA circular loop is placed in magnetic field B=2t. Find the direction of induced current produced in the loop.

View SolutionCurrent I is flowing through a circular coil of radius r. It is placed in a magnetic field B in such a way that the plane of the circular coil is perpendicular to B. The force acting on it will be -
View Solution
