If decompositon reaction A(g)toB(g) follows first order linetics then the graph of rate of formation (R ) of B against time t will be :

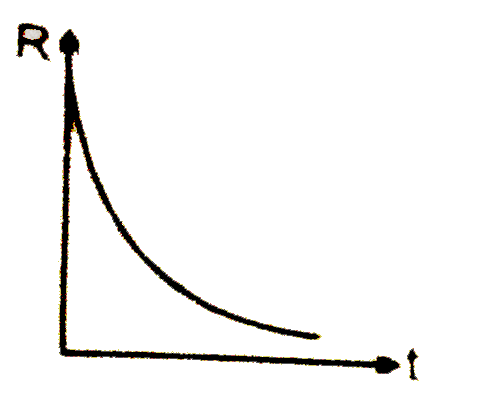
The correct Answer is:C
To solve the problem, we need to analyze the decomposition reaction A(g)→B(g) that follows first-order kinetics. We want to determine the graph of the rate of formation of B against time t.
1. Understanding First-Order Kinetics:
- For a first-order reaction, the rate of reaction is directly proportional to the concentration of the reactant. This can be expressed mathematically as:
−d(A)dt=k(A)
- Here, k is the rate constant, and (A) is the concentration of A.
2. Relating the Formation of B:
- The rate of formation of B is equal to the rate of consumption of A:
d(B)dt=−d(A)dt
- Therefore, we can write:
d(B)dt=k(A)
3. Expressing Concentration of A:
- For a first-order reaction, the concentration of A at any time t can be expressed as:
(A)=(A0)e−kt
- Here, (A0) is the initial concentration of A.
4. Substituting into the Rate Equation:
- Substituting the expression for (A) into the rate of formation of B:
d(B)dt=k(A0)e−kt
- This shows that the rate of formation of B is also an exponential function of time.
5. Graphing the Rate of Formation:
- The equation d(B)dt=k(A0)e−kt indicates that the rate of formation of B decreases exponentially over time.
- Therefore, if we plot the rate of formation of B (on the y-axis) against time t (on the x-axis), we will get a graph that starts at a maximum value (when t=0) and decreases towards zero as time progresses.
Conclusion:
The graph of the rate of formation of B against time t will be an exponential decay curve.
- For a first-order reaction, the rate of reaction is directly proportional to the concentration of the reactant. This can be expressed mathematically as:
−d(A)dt=k(A)
- Here, k is the rate constant, and (A) is the concentration of A.
- The rate of formation of B is equal to the rate of consumption of A:
d(B)dt=−d(A)dt
- Therefore, we can write:
d(B)dt=k(A)
- For a first-order reaction, the concentration of A at any time t can be expressed as:
(A)=(A0)e−kt
- Here, (A0) is the initial concentration of A.
- Substituting the expression for (A) into the rate of formation of B:
d(B)dt=k(A0)e−kt
- This shows that the rate of formation of B is also an exponential function of time.
- The equation d(B)dt=k(A0)e−kt indicates that the rate of formation of B decreases exponentially over time.
- Therefore, if we plot the rate of formation of B (on the y-axis) against time t (on the x-axis), we will get a graph that starts at a maximum value (when t=0) and decreases towards zero as time progresses.
The graph of the rate of formation of B against time t will be an exponential decay curve.
Similar Questions
Knowledge Check
Consider a first order gas phase decomposition reaction given below:
A(g)→B(g)+C(g)
The initial pressure of the system before decomposition of A was pi. After lapse of time 'T', total pressure of the system increased by x units and became 'pt'. The rate constant k for the reaction is given asAk=2.303tlogpipI−xBk=2.303tlog2pipI−xCk=2.303tlogpipI−ptDk=2.303tlogpipi−xConsider a first order gas phase decomposition reaction given below:
A(g)→B(g)+C(g)
The initial pressure of the system before decomposition of A was pi. After lapse of time 'T', total pressure of the system increased by x units and became 'pt'. The rate constant k for the reaction is given asAk=2.303tlogpipI−xBk=2.303tlog2pipI−xCk=2.303tlogpipI−ptDk=2.303tlogpipi−xConsider a first order gas phase decomposition reaction given below:
A(g)→B(g)+C(g)
The initial pressure of the system before decomposition of A was pi. After lapse of time 'T', total pressure of the system increased by x units and became 'pt'. The rate constant k for the reaction is given asAk=2.303tlogpipI−xBk=2.303tlog2pipI−xCk=2.303tlogpipI−ptDk=2.303tlogpipi−x
The rate of decomposition of NH3(g) at 10 atm on platinum surface is zero order . What is rate of formation (in M −1min) of H2(g) , if rate constant of reaction 2NH3(g)→N2(g)+3H2(g) is 2.0 M −1min?
View SolutionThe decomposition of a gaseous substance A yields gaseous products as shown, A(g) →2 B(g) + C(g) . This reaction follows first order kinetics. If the total pressure at the start of the experiment & 9 minutes after the start are 169 mm and 221 mm, what is the value of rate constant?
View SolutionConsider a first order gas phase decompostion reaction gives below
A(g)→B(g)→C(g)
The initial pressure of the system before decomposition of A pi. After lapse of time 't' total pressure of the system increased by x units and became pt. The rate constant K for the reaction is given as....... .
View SolutionConsider a first order gas phase decomposition reaction given below:
A(g)→Bg+Cg
The initial pressure of the system before decomposition of A was pi. After lapse of time t'. Total pressure of the system increased by x units and became Pt. the rate constant k for the reaction is given as
View SolutionA reaction in which reactants (R ) are converted into products (P) follows second order kinetics. If concentration of R is increased by four times, what will be the increase in the rate formation of p?
View Solution
