A radioactiev nuleus X deays to a stable nuleus Y. Then, time graph of rate of formation of Y against time t will be:
The correct Answer is:c
To solve the problem of determining the time graph of the rate of formation of stable nucleus Y from radioactive nucleus X, we can follow these steps:
Step 1: Understand the Decay Process
Radioactive nucleus X decays over time into stable nucleus Y. The decay process can be described by the exponential decay law, which states that the number of radioactive nuclei decreases over time.
Step 2: Write the Decay Law
The number of undecayed nuclei N(t) at time t can be expressed as:
N(t)=N0e−αt
where N0 is the initial number of nuclei, and α is the decay constant.
Step 3: Determine the Rate of Formation of Y
As nucleus X decays, nucleus Y is formed. The rate of formation of Y, RY(t), is equal to the rate of decay of X, which can be expressed as:
RY(t)=−dN(t)dt
Calculating this derivative gives:
RY(t)=αN0e−αt
This shows that the rate of formation of Y is proportional to the number of undecayed nuclei of X.
Step 4: Analyze the Graph of RY(t)
From the equation RY(t)=αN0e−αt, we can see that:
- At t=0, RY(0)=αN0 (maximum rate of formation).
- As time increases, e−αt decreases, leading to a decrease in RY(t).
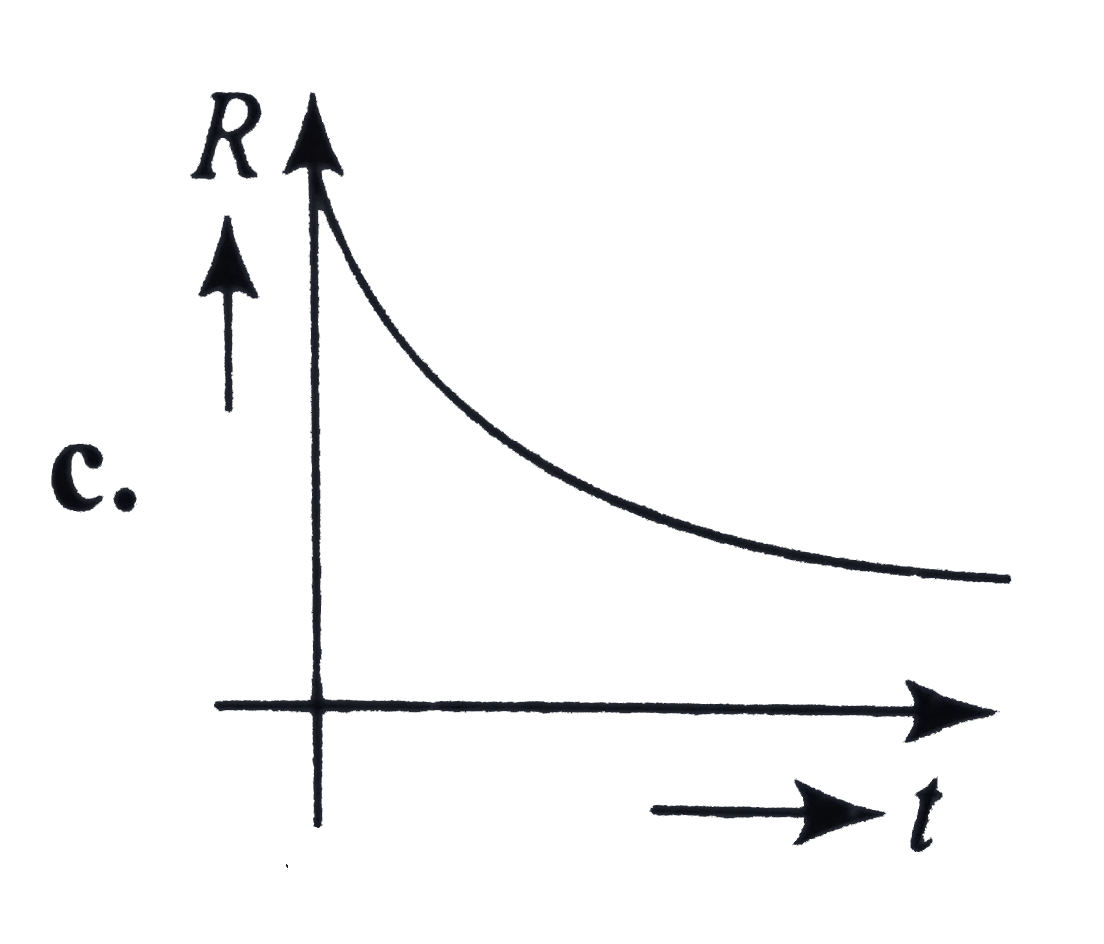
Step 5: Sketch the Graph
The graph of RY(t) against time t will start at a maximum value when t=0 and will decrease exponentially towards zero as time progresses. This graph will resemble a decaying exponential curve.
Conclusion
Thus, the time graph of the rate of formation of Y against time t will show a decreasing exponential trend.
Final Answer
The correct option for the graph of the rate of formation of Y against time is option C.
---
Radioactive nucleus X decays over time into stable nucleus Y. The decay process can be described by the exponential decay law, which states that the number of radioactive nuclei decreases over time.
The number of undecayed nuclei N(t) at time t can be expressed as:
N(t)=N0e−αt
where N0 is the initial number of nuclei, and α is the decay constant.
As nucleus X decays, nucleus Y is formed. The rate of formation of Y, RY(t), is equal to the rate of decay of X, which can be expressed as:
RY(t)=−dN(t)dt
Calculating this derivative gives:
RY(t)=αN0e−αt
This shows that the rate of formation of Y is proportional to the number of undecayed nuclei of X.
From the equation RY(t)=αN0e−αt, we can see that:
- At t=0, RY(0)=αN0 (maximum rate of formation).
- As time increases, e−αt decreases, leading to a decrease in RY(t).
The graph of RY(t) against time t will start at a maximum value when t=0 and will decrease exponentially towards zero as time progresses. This graph will resemble a decaying exponential curve.
Thus, the time graph of the rate of formation of Y against time t will show a decreasing exponential trend.
The correct option for the graph of the rate of formation of Y against time is option C.
Topper's Solved these Questions
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - NUCLEAR PHYSICSEXERCISE - Linked Comprehension29videos
NUCLEAR PHYSICS
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - NUCLEAR PHYSICSEXERCISE - Integer6videos
NUCLEAR PHYSICS
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - NUCLEAR PHYSICSEXERCISE - Subjective35videos
NUCLEAR PHYSICS
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - MISCELLANEOUS VOLUME 5EXERCISE - Integer12videos
MISCELLANEOUS VOLUME 5
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - PHOTOELECTRIC EFFECTEXERCISE - Integer Type4videos
PHOTOELECTRIC EFFECT
Similar Questions
Knowledge Check
- Question 1 - Select One
A radioactive element X with half life 2 h decays giving a stable element Y. After a time t, ratio of X and Y atoms is 1:16 .Time t is
A6 hB4 hC8 hD16 h
The graph represents the decay of a newly-prepared sample of radioactive nuclide X to a stable nuclide Y. The half-life of X is t. The growth curve for Y intersects the decay curve for X after time T. What is the time T ?
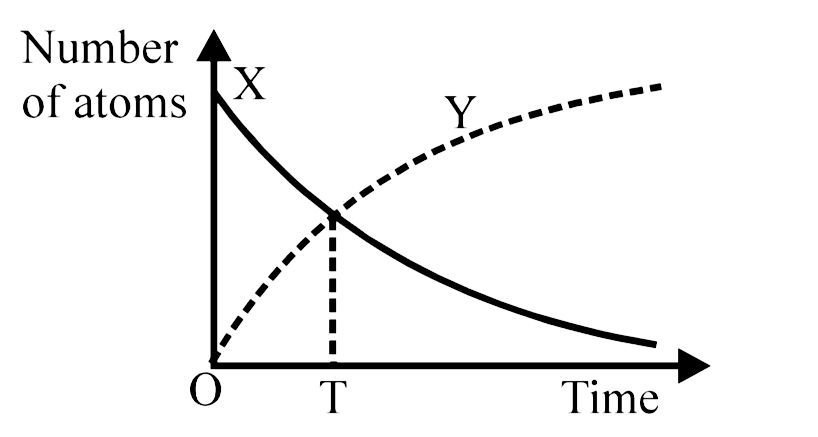 View Solution
View SolutionA radioactive nucleus X decays to a nucleus Y with a decay constant λX=0.1s−1, Y further decays to a stable nucleus Z with a decay constant
λY=1/30s−1. Initially, there are only X nuclei and their number is N0=1020. Set up the rate equations for the populations of X, Y and Z. The population of Y nucleus as a function of time is given by NY(t)={N0λX/(λX−λY)}[exp(−λYt)−exp(−λXt)].
Find the time at which NY is maximum and determine the population X and Z at that instant.View SolutionNuclei of a radioactive element X are being produced at a constant rate K and this element decays to a stable nucleus Y with a decay constant λ and half-life T1/3. At the time t=0, there are N0nuclei of the element X.
The number NY of nuclei of Y at time t is .View SolutionNuclei of a radioactive element X are being produced at a constant rate K and this element decays to a stable nucleus Y with a decay constant λ and half-life T1/2. At the time t=0, there are N0nuclei of the element X.
The number NX of nuclei of X at time t=T1/2 is .View SolutionA stone is projected at time t=0 with a speed v0 at an angle θ with the horizontal in a uniform gravitational field. The rate of work done (P) by the gravitational force plotted against time (t) will be as.
View SolutionA radioactive elementX converts into another stable elemnet Y. Half-life of X is 2h. Initally, only X is present. After time t, the ratio of atoms of X and Y is found to be 1:4 Then t in hours is .
View SolutionNuclei X and Y convert into a stable nucleus Z. At t=0 , the number of nuclei of X is 8 times that of Y. Half life of X is 1 hour and half life of y=2 hour. Find the time (in hour) at which rate of disintegration of X and Y are equal.
View Solution

