In diamond structure ,carbon atoms form fcc lattic and 50% tetrahedral voids occupied by acrbon atoms . Evergy carbon atoms is surrounded tetrachedral by four carbon atom with bond length 154 pm . Germanium , silicon and grey tin also crystallise in same way as diamond (NA=6×1023)
The side length of diamond unit cell (in pm):
a. 154
b. 1422.63
c. 711.32
d. 355.66
The correct Answer is:D
To find the side length of the diamond unit cell, we can follow these steps:
Step 1: Understand the structure
The diamond structure is based on a face-centered cubic (FCC) lattice. In this structure, each carbon atom is tetrahedrally coordinated with four other carbon atoms.
Step 2: Identify the relationship between edge length and atomic radius
In an FCC lattice, the relationship between the edge length (a) and the radius (r) of the atoms is given by the formula:
√34a=2r
This formula accounts for the tetrahedral arrangement of atoms in the diamond structure.
Step 3: Rearrange the formula to find edge length
From the formula, we can rearrange it to solve for the edge length (a):
a=2r⋅4√3=8r√3
Step 4: Substitute the bond length
The bond length between carbon atoms is given as 154 pm. Since this bond length corresponds to the distance between two carbon atoms, we can consider this as twice the radius (r):
r=154 pm2=77 pm
Step 5: Calculate the edge length
Now, substituting the value of r into the equation for a:
a=8×77 pm√3=616 pm√3≈355.66 pm
Step 6: Conclusion
Thus, the side length of the diamond unit cell is approximately 355.66 pm.
Final Answer
The side length of the diamond unit cell is d. 355.66 pm.
---
The diamond structure is based on a face-centered cubic (FCC) lattice. In this structure, each carbon atom is tetrahedrally coordinated with four other carbon atoms.
In an FCC lattice, the relationship between the edge length (a) and the radius (r) of the atoms is given by the formula:
√34a=2r
This formula accounts for the tetrahedral arrangement of atoms in the diamond structure.
From the formula, we can rearrange it to solve for the edge length (a):
a=2r⋅4√3=8r√3
The bond length between carbon atoms is given as 154 pm. Since this bond length corresponds to the distance between two carbon atoms, we can consider this as twice the radius (r):
r=154 pm2=77 pm
Now, substituting the value of r into the equation for a:
a=8×77 pm√3=616 pm√3≈355.66 pm
Thus, the side length of the diamond unit cell is approximately 355.66 pm.
The side length of the diamond unit cell is d. 355.66 pm.
Topper's Solved these Questions
- SOLID STATEBook:NARENDRA AWASTHI ENGLISHChapter:SOLID STATEExercise:One or More Anwer is / correct
Explore 20 Videos
- SOLID STATEBook:NARENDRA AWASTHI ENGLISHChapter:SOLID STATEExercise:Match the column
Explore 10 Videos
- SOLID STATEBook:NARENDRA AWASTHI ENGLISHChapter:SOLID STATEExercise:Passage-6
Explore 2 Videos
- IONIC EEQUILIBRIUMBook:NARENDRA AWASTHI ENGLISHChapter:IONIC EEQUILIBRIUMExercise:Subjective problems
Explore 1 Video
- STOICHIOMETRYBook:NARENDRA AWASTHI ENGLISHChapter:STOICHIOMETRYExercise:Match the Colum-II
Explore 6 Videos
Similar Questions
In diamond structure ,carbon atoms form fcc lattic and 50% tetrahedral voids occupied by acrbon atoms . Evergy carbon atoms is surrounded tetrachedral by four carbon atom with bond length 154 pm . Germanium , silicon and grey tin also crystallise in same way as diamond (NA=6×1023)
The mass of diamond unit cell is:
View SolutionIn diamond structure ,carbon atoms form fcc lattic and 50% tetrahedral voids occupied by acrbon atoms . Evergy carbon atoms is surrounded tetrachedral by four carbon atom with bond length 154 pm . Germanium , silicon and tin also crystallise in same way as diamond (NA=6×1023)
The side length of diamond unit cell is (in pm):
View SolutionPercentage of tetrahedral voids occupied by carbon atoms per unit cell of diamond is
View SolutionOnly those atoms which four covalent bonds produce a repetitive three dimesional structure using only covalent bonds., e.g. , diamond structure.The latter is based on a FCC lattice where lattice points are occupied by carbon atoms.Every atom in this structure is surrounded tetrahedrally by four others.Germanium, silicon and grey tin also crystallize in the same way as diamond. (Given :NA=6×1023sin54∘44'=0.8164)
If edge length of the cube is 3.60Å, then radius of carbon atom is
View SolutionOnly those atoms which four covalent bonds produce a repetitive three dimesional structure using only covalent bonds., e.g. , diamond structure.The latter is based on a FCC lattice where lattice points are occupied by carbon atoms.Every atom in this structure is surrounded tetrahedrally by four others.Germanium, silicon and grey tin also crystallize in the same way as diamond. (Given :NA=6×1023sin54∘44'=0.8164)
If the edge length is 3.60Å, density of diamond crystal is
View SolutionNumber of octahedral void(s) occupied by carbon atoms in the unit cell of diamond is
View SolutionTetrahedral voids is surrounded by four atoms. Which atoms in the given figure are around the tetrahedral voids ?
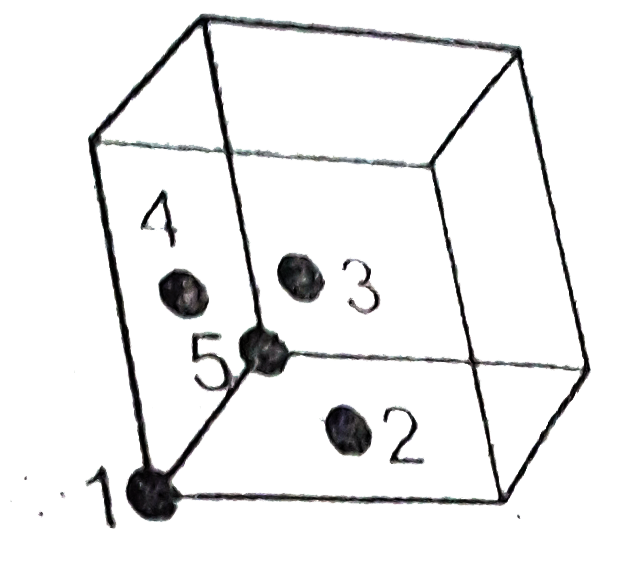
View SolutionIn a crystal of diamond :
How many carbon atoms surround each carbon atom
View SolutionIn a diamond, each carbon atom is bonded to four other carbon atoms tetrahedrally. Alternate tetrahedral voids are occupied by carbon atoms. The number of carbon atoms per unit cell is:
View SolutionNumber of tetrahedral voids occupied in a unit cell of diamond is
View Solution
