Only those atoms which four covalent bonds produce a repetitive three dimesional structure using only covalent bonds., e.g. , diamond structure.The latter is based on a FCC lattice where lattice points are occupied by carbon atoms.Every atom in this structure is surrounded tetrahedrally by four others.Germanium, silicon and grey tin also crystallize in the same way as diamond. (Given :NA=6×1023sin54∘44'=0.8164)
If the edge length is 3.60Å, density of diamond crystal is
3.92 gm/cc
2.40 gm/cc
3.37 gm/cc
2.58 gm/cc
The correct Answer is:C
To find the density of diamond crystal, we will follow these steps:
Step 1: Write down the given data
- Edge length (A) = 3.60 Å
- Avogadro's number (N_A) = 6 × 10^23 sin(54° 44') = 0.8164
- Mass of carbon atom (M_A) = 12 g/mol
Step 2: Convert edge length to centimeters
Since 1 Å = 10^-8 cm, we convert the edge length:
A=3.60Å=3.60×10−8cm
Step 3: Calculate the volume of the unit cell
The volume (V) of the cubic unit cell is given by:
V=A3
Substituting the value of A:
V=(3.60×10−8cm)3=4.6656×10−24cm3
Step 4: Determine the number of atoms per unit cell (Z)
For diamond, which has a face-centered cubic (FCC) structure:
- There are 8 atoms at the corners, each contributing 18 of an atom:
8×18=1
- There are 6 atoms at the face centers, each contributing 12 of an atom:
6×12=3
- Additionally, there are 4 atoms that are not shared by any other atoms, contributing 4:
Z=1+3+4=8
Step 5: Calculate the mass of the unit cell
The mass of the unit cell (m) can be calculated using:
m=Z×mass of one carbon atom
Converting the mass of carbon to grams:
m=8×12g/mol=96g/mol
To convert this to grams for the unit cell, we use Avogadro's number:
mass of unit cell=96g/molNA=966×1023=1.6×10−22g
Step 6: Calculate the density (ρ)
Density is given by the formula:
ρ=mass of unit cellvolume of unit cell
Substituting the values:
ρ=1.6×10−22g4.6656×10−24cm3
Calculating this gives:
ρ≈3.43g/cm3
Final Answer
The density of diamond crystal is approximately 3.43 g/cm³.
---
- Edge length (A) = 3.60 Å
- Avogadro's number (N_A) = 6 × 10^23 sin(54° 44') = 0.8164
- Mass of carbon atom (M_A) = 12 g/mol
Since 1 Å = 10^-8 cm, we convert the edge length:
A=3.60Å=3.60×10−8cm
The volume (V) of the cubic unit cell is given by:
V=A3
Substituting the value of A:
V=(3.60×10−8cm)3=4.6656×10−24cm3
For diamond, which has a face-centered cubic (FCC) structure:
- There are 8 atoms at the corners, each contributing 18 of an atom:
8×18=1
- There are 6 atoms at the face centers, each contributing 12 of an atom:
6×12=3
- Additionally, there are 4 atoms that are not shared by any other atoms, contributing 4:
Z=1+3+4=8
The mass of the unit cell (m) can be calculated using:
m=Z×mass of one carbon atom
Converting the mass of carbon to grams:
m=8×12g/mol=96g/mol
To convert this to grams for the unit cell, we use Avogadro's number:
mass of unit cell=96g/molNA=966×1023=1.6×10−22g
Density is given by the formula:
ρ=mass of unit cellvolume of unit cell
Substituting the values:
ρ=1.6×10−22g4.6656×10−24cm3
Calculating this gives:
ρ≈3.43g/cm3
The density of diamond crystal is approximately 3.43 g/cm³.
Topper's Solved these Questions
Similar Questions
Only those atoms which four covalent bonds produce a repetitive three dimesional structure using only covalent bonds., e.g. , diamond structure.The latter is based on a FCC lattice where lattice points are occupied by carbon atoms.Every atom in this structure is surrounded tetrahedrally by four others.Germanium, silicon and grey tin also crystallize in the same way as diamond. (Given :NA=6×1023sin54∘44'=0.8164)
If edge length of the cube is 3.60Å, then radius of carbon atom is
View SolutionIn a covalent solid the lattice points are occupied by
View SolutionIn diamond structure ,carbon atoms form fcc lattic and 50% tetrahedral voids occupied by acrbon atoms . Evergy carbon atoms is surrounded tetrachedral by four carbon atom with bond length 154 pm . Germanium , silicon and grey tin also crystallise in same way as diamond (NA=6×1023)
The mass of diamond unit cell is:
View SolutionIn diamond structure ,carbon atoms form fcc lattic and 50% tetrahedral voids occupied by acrbon atoms . Evergy carbon atoms is surrounded tetrachedral by four carbon atom with bond length 154 pm . Germanium , silicon and tin also crystallise in same way as diamond (NA=6×1023)
The side length of diamond unit cell is (in pm):
View SolutionIn diamond structure ,carbon atoms form fcc lattic and 50% tetrahedral voids occupied by acrbon atoms . Evergy carbon atoms is surrounded tetrachedral by four carbon atom with bond length 154 pm . Germanium , silicon and grey tin also crystallise in same way as diamond (NA=6×1023)
The side length of diamond unit cell (in pm):
a. 154
b. 1422.63
c. 711.32
d. 355.66
View SolutionPercentage of tetrahedral voids occupied by carbon atoms per unit cell of diamond is
View SolutionTetrahedral voids is surrounded by four atoms. Which atoms in the given figure are around the tetrahedral voids ?
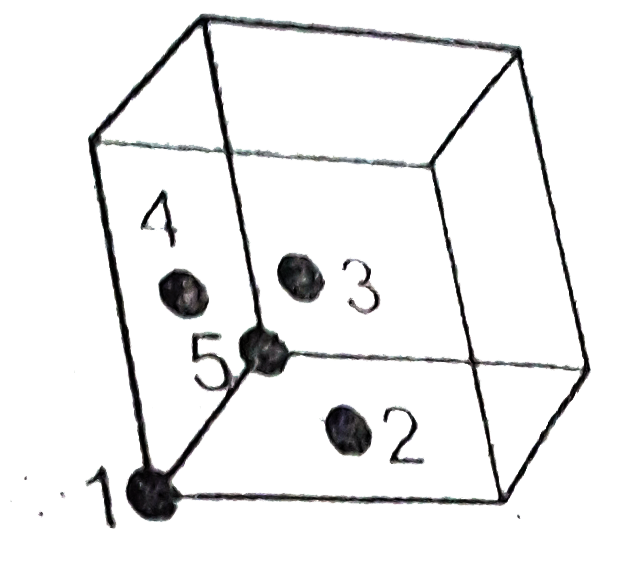
View SolutionNumber of octahedral void(s) occupied by carbon atoms in the unit cell of diamond is
View SolutionIn a diamond, each carbon atom is bonded to four other carbon atoms tetrahedrally. Alternate tetrahedral voids are occupied by carbon atoms. The number of carbon atoms per unit cell is:
View SolutionDiamond is hard because all the four valence electrons are bonded to four carbon atoms by comvlent bonds .
View Solution
