Force displacement graph of a particle starting from rest is given in the figure shown.The kinetic energy of particle at x=3m is: (A) 6.5 J (B) 7.5 J (C) 6 J (D) 5 J
To find the kinetic energy of a particle at x=3m using the force-displacement graph, we can follow these steps:
1. Understand the Problem:
The particle starts from rest, meaning its initial velocity u=0. We need to find the kinetic energy at x=3m.
2. Work-Energy Theorem:
According to the work-energy theorem, the change in kinetic energy (ΔK) is equal to the work done on the particle:
ΔK=W
where W is the work done.
3. Calculate Work Done:
The work done can be calculated as the area under the force-displacement graph. We need to find the area of the shapes formed in the graph up to x=3m.
4. Identify Areas:
- The first shape is a rectangle with a base of 2m and height 2N:
Arearectangle=base×height=2m×2N=4J
- The second shape is a trapezium with bases of 2N and 3N, and a height of 1m:
Areatrapezium=12×(base1+base2)×height=12×(2+3)×1=52=2.5J
5. Total Work Done:
Now, we sum the areas to find the total work done:
W=Arearectangle+Areatrapezium=4J+2.5J=6.5J
6. Calculate Kinetic Energy:
Since the particle starts from rest, the change in kinetic energy is equal to the work done:
ΔK=K−K0=W
where K0=0 (initial kinetic energy). Thus,
K=W=6.5J
Conclusion:
The kinetic energy of the particle at x=3m is 6.5J. Therefore, the correct answer is (A) 6.5 J.
The particle starts from rest, meaning its initial velocity u=0. We need to find the kinetic energy at x=3m.
According to the work-energy theorem, the change in kinetic energy (ΔK) is equal to the work done on the particle:
ΔK=W
where W is the work done.
The work done can be calculated as the area under the force-displacement graph. We need to find the area of the shapes formed in the graph up to x=3m.
- The first shape is a rectangle with a base of 2m and height 2N:
Arearectangle=base×height=2m×2N=4J
- The second shape is a trapezium with bases of 2N and 3N, and a height of 1m:
Areatrapezium=12×(base1+base2)×height=12×(2+3)×1=52=2.5J
Now, we sum the areas to find the total work done:
W=Arearectangle+Areatrapezium=4J+2.5J=6.5J
Since the particle starts from rest, the change in kinetic energy is equal to the work done:
ΔK=K−K0=W
where K0=0 (initial kinetic energy). Thus,
K=W=6.5J
The kinetic energy of the particle at x=3m is 6.5J. Therefore, the correct answer is (A) 6.5 J.
Similar Questions
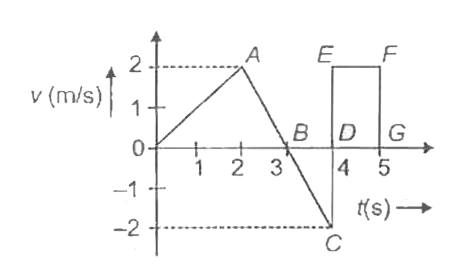
The velocity - time graph of a particle moving along a straight line is shown in the figure given below
The displacement of the particle in 5 second is
View SolutionThe potential energy of a particle executing S H M is 25 J. when its displacement is half of amplitude. The total energy of the particle is
View Solution
Knowledge Check
The energy of a particle moving at 5 m/s is 125 J. The mass is
A4kgB6 kgC10 kgD25 kgA ancleus of mass number 220, initially at rest, emits an α-particle, If the Q-value of the reaction is 5.5 Me V, then the energy of the emitted α-particle will be
A4.4 MeVB5.4 MeVC5.6 MeVD6.5 MeV
The potential energy of a particle execuring S.H.M. is 5 J, when its displacement is half of amplitude. The total energy of the particle be
View SolutionThe P.E. of an oscillation particle at rest position is 10J and its average K.E. is 5J. The total energy of particle at any instant will be-
View SolutionThe potential energy of a particle executing S.H.M. is 2.5 J, when its displacement is half of amplitude. The total energy of the particle will be
View SolutionFind the kinetic energy of a particle of mass 200g moving with velocity 3ˆi−5ˆj+4ˆkm/s.
View SolutionA Force F acting on an object varies with distance x as shown in the figure . The force is in newton and x in metre. The work done by the force in moving the object from x=0 to x=6m is
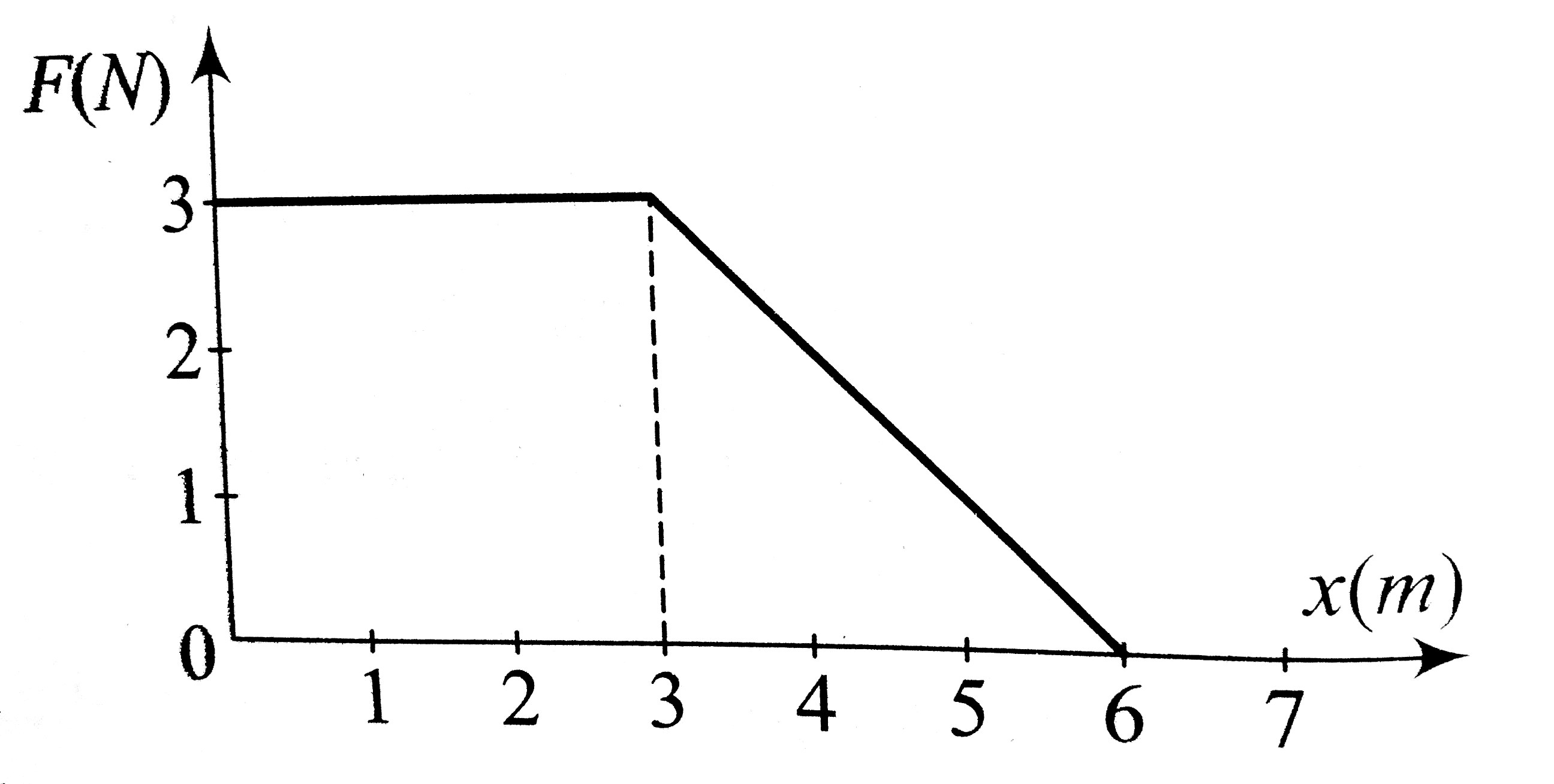
(a) 4.5 J (b) 13.5 J (c) 9.0 J (d) 18.0 J
View SolutionIn simple harmonic motion of a particle, maximum kinetic energy is 40 J and maximum potential energy is 60 J. then
View Solution
