if current in solenoid is i1=αteβt. Which of the followign is correct graph between induced current rod time (α and β are positive)
_2019_CBT4_E01_085_O01.png)
_2019_CBT4_E01_085_O02.png)
_2019_CBT4_E01_085_O03.png)
_2019_CBT4_E01_085_O04.png)
The correct Answer is:A
To solve the problem, we need to find the induced current in the solenoid based on the given current i1=αteβt. The induced current is given by the rate of change of the current with respect to time, which is mathematically represented as:
Iinduced=dI1dt
Step 1: Differentiate the current i1
Given:
I1=αteβt
We will use the product rule for differentiation, which states that if you have a product of two functions u(t) and v(t), then:
d(uv)dt=udvdt+vdudt
Here, let:
- u=αt
- v=eβt
Now, we differentiate u and v:
dudt=αanddvdt=βeβt
Using the product rule:
dI1dt=udvdt+vdudt
Substituting the values:
dI1dt=(αt)(βeβt)+(eβt)(α)
Step 2: Simplify the expression
Now, factor out the common terms:
dI1dt=αeβt(tβ+1)
Step 3: Analyze the expression
Now we have:
Iinduced=αeβt(tβ+1)
Step 4: Determine the sign of the induced current
1. At t=0:
Iinduced=αe0(0⋅β+1)=α⋅1⋅1=α
Since α>0, Iinduced>0.
2. As t increases:
- The term eβt is always positive for positive β.
- The term (tβ+1) will also be positive for t>0 since t is positive and β is positive.
Thus, Iinduced is positive for all t≥0.
Conclusion
The correct graph of the induced current with respect to time will start from a positive value at t=0 and will continue to increase as t increases.
I1=αteβt
- u=αt
- v=eβt
Iinduced=αe0(0⋅β+1)=α⋅1⋅1=α
Since α>0, Iinduced>0.
- The term eβt is always positive for positive β.
- The term (tβ+1) will also be positive for t>0 since t is positive and β is positive.
Topper's Solved these Questions
Similar Questions
The correct relationship between the two current gains αandβ in a transistor is
View SolutionPotential energy of a system of particles is U=α3r3−β2r2, where r is distance between the particles. Here αandβ are positive constants. Which of the following are correct for the system?
View SolutionA conducting rod is rotated about one end in a plane perpendicular to a uniform magnetic field with constant angular velocity. The correct graph between the induced emf (e) across the rod and time (t) is
View SolutionThe current i in an induction coil varies with time according to the graph shown in figure. Which of the following graph shows induced emf in the coil with time:
View SolutionThe current i in an inductionn coil varies with time t according to the graph shown in the figure. Which of the following grahs shows athe induced emf (ε) in the coil with time?
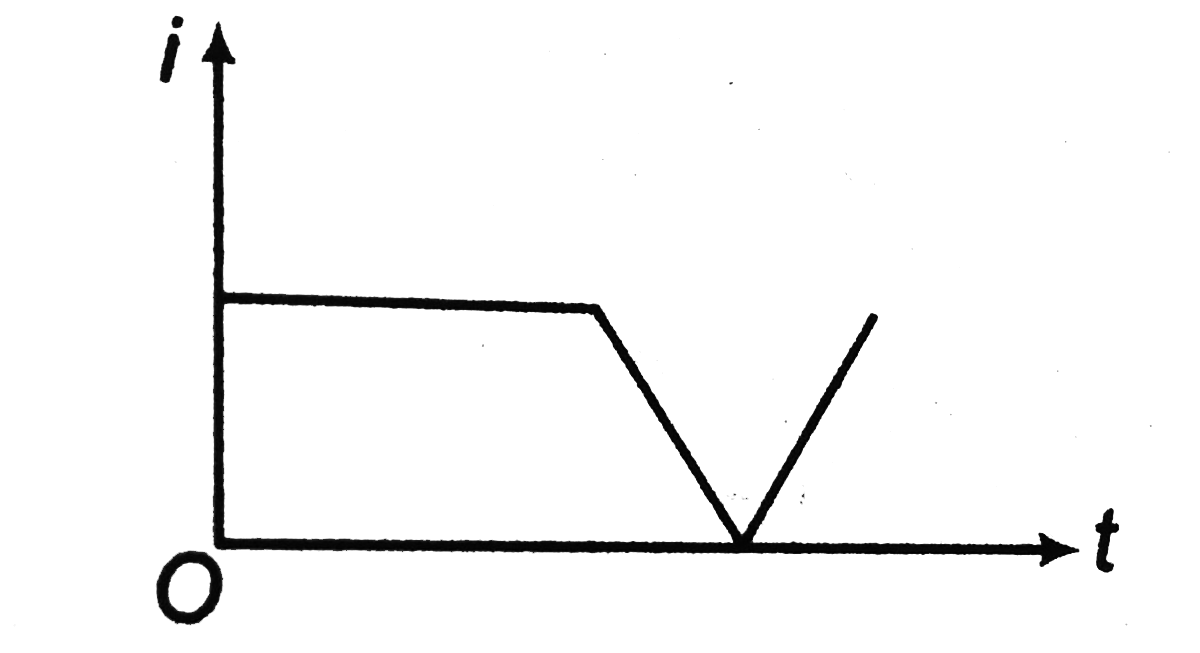
View SolutionThe current i in an inductionn coil varies with time t according to the graph shown in the figure. Which of the following grahs shows athe induced emf (ε) in the coil with time?

View SolutionA constant current I is maintained in a solenoid. Which of lthe following quantities will increase if an iron rod is inserted in the solenoid along its axis?
View SolutionThe energy E of a particle varies with time t according to the equation E=E0sin(αt).e−αtβx, where x is displacement from mean position E0 is energy at infinite position and α and β are constants .
Dimensions of sin(αtβx) are
View SolutionThe energy E of a particle varies with time t according to the equation E=E0sin(αt).e−αtβx, where x is displacement from mean position E0 is energy at infinite position and α and β are constants .
Dimensions of β are
View SolutionThe energy E of a particle varies with time t according to the equation E=E0sin(αt).e−αtβx, where x is displacement from mean position E0 is energy at infinite position and α and β are constants .
Dimensional formula of α is
View Solution
