A projectile is projected upward with speed 2m/s on an incline plane of inclination 30∘ at an angle of 15∘ from the plane. Then the distance along the plane where projectile will fall is :
415
45(1√3−13)
45(1√3−13)
4√3(1√3−13)
The correct Answer is:C
To solve the problem of finding the distance along the incline where the projectile will fall, we will use the range formula for projectile motion on an inclined plane. Let's break down the steps:
Step 1: Identify the parameters
- Initial speed u=2m/s
- Angle of projection from the incline α=15∘
- Angle of inclination of the plane β=30∘
- Acceleration due to gravity g=10m/s2
Step 2: Use the range formula for projectile motion on an inclined plane
The formula for the range R of a projectile launched at an angle α on an incline with angle β is given by:
R=2u2sinαcos(α+β)gcos2β
Step 3: Calculate the necessary trigonometric values
1. Calculate sinα:
sin(15∘)=√6−√24
2. Calculate cos(α+β):
α+β=15∘+30∘=45∘
cos(45∘)=1√2
3. Calculate cos2β:
cos(30∘)=√32
cos2(30∘)=(√32)2=34
Step 4: Substitute the values into the range formula
Now we substitute the values into the range formula:
R=2⋅(22)⋅(√6−√24)⋅(1√2)10⋅34
Step 5: Simplify the expression
1. Calculate 2⋅(22)=8.
2. The denominator becomes 10⋅34=304=7.5.
3. The numerator becomes:
8⋅√6−√24⋅1√2=2⋅√6−√2√2=2(√6−√2)√2
4. Therefore, we have:
R=2(√6−√2)√27.5
Step 6: Final calculation
Now we can simplify further:
R=2(√6−√2)7.5√2=2(√6−√2)15/2=4(√6−√2)15
Conclusion
Thus, the distance along the incline where the projectile will fall is given by:
R=4(√6−√2)15meters
- Initial speed u=2m/s
- Angle of projection from the incline α=15∘
- Angle of inclination of the plane β=30∘
- Acceleration due to gravity g=10m/s2
The formula for the range R of a projectile launched at an angle α on an incline with angle β is given by:
1. Calculate sinα:
sin(15∘)=√6−√24
2. Calculate cos(α+β):
α+β=15∘+30∘=45∘
cos(45∘)=1√2
cos(30∘)=√32
cos2(30∘)=(√32)2=34
Now we substitute the values into the range formula:
1. Calculate 2⋅(22)=8.
2. The denominator becomes 10⋅34=304=7.5.
3. The numerator becomes:
8⋅√6−√24⋅1√2=2⋅√6−√2√2=2(√6−√2)√2
R=2(√6−√2)√27.5
Now we can simplify further:
R=2(√6−√2)7.5√2=2(√6−√2)15/2=4(√6−√2)15
Thus, the distance along the incline where the projectile will fall is given by:
R=4(√6−√2)15meters
Topper's Solved these Questions
Similar Questions
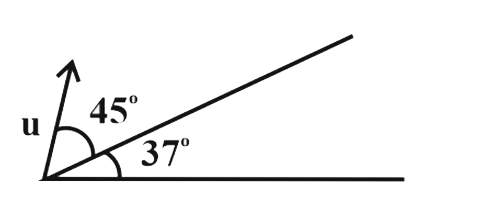
A particle is projected on a frictionless inclined plane of inclination 37∘ at an angle of projection 45∘ from the inclined plane as shown in the figure. If after the first collision from the plane, the particle returns to its point of projection, then what is the value of the reciprocal of the coefficient of restitution between the particle and the plane?
View SolutionA particle is projected from the bottom of an inclined plane of inclination 30∘ with velocity of 40m/s at an angle of 60∘ with horizontal. Find the speed of the particle when its velocity vector is parallel to the plane. Take g=10m/s2.
View SolutionA particle is projected from the bottom of an inclined plane of inclination 30∘. At what angle α (from the horizontal) should the particle be projected to get the maximum range on the inclined plane.
View SolutionA ball is projected from the bottom of an inclined plane of inclination 30∘, with a velocity of 30ms−1, at an angle of 30∘ with the inclined plane. If g=10ms−2 , then the range of the ball on given inclined plane is
View SolutionThe maximum range of a projectile is 500m. If the particle is thrown up a plane is inclined at an angle of 30∘ with the same speed, the distance covered by it along the inclined plane will be:
View SolutionA projectile si thrown with velocity of 50m/s towards an inclined plane from ground such that is strikes the inclined plane perpendiclularly. The angle of projection of the projectile is 53∘ with the horizontal and the inclined plane is inclined at an angle of 45∘ to the horizonta..

(a) Find the time of flight.
(b) Find the distance between the point of projection and the foot of inclined plane.
View SolutionA ball is projected horizontally with a speed v from the top of the plane inclined at an angle 45∘ with the horizontal. How far from the point of projection will the ball strikes the plane?
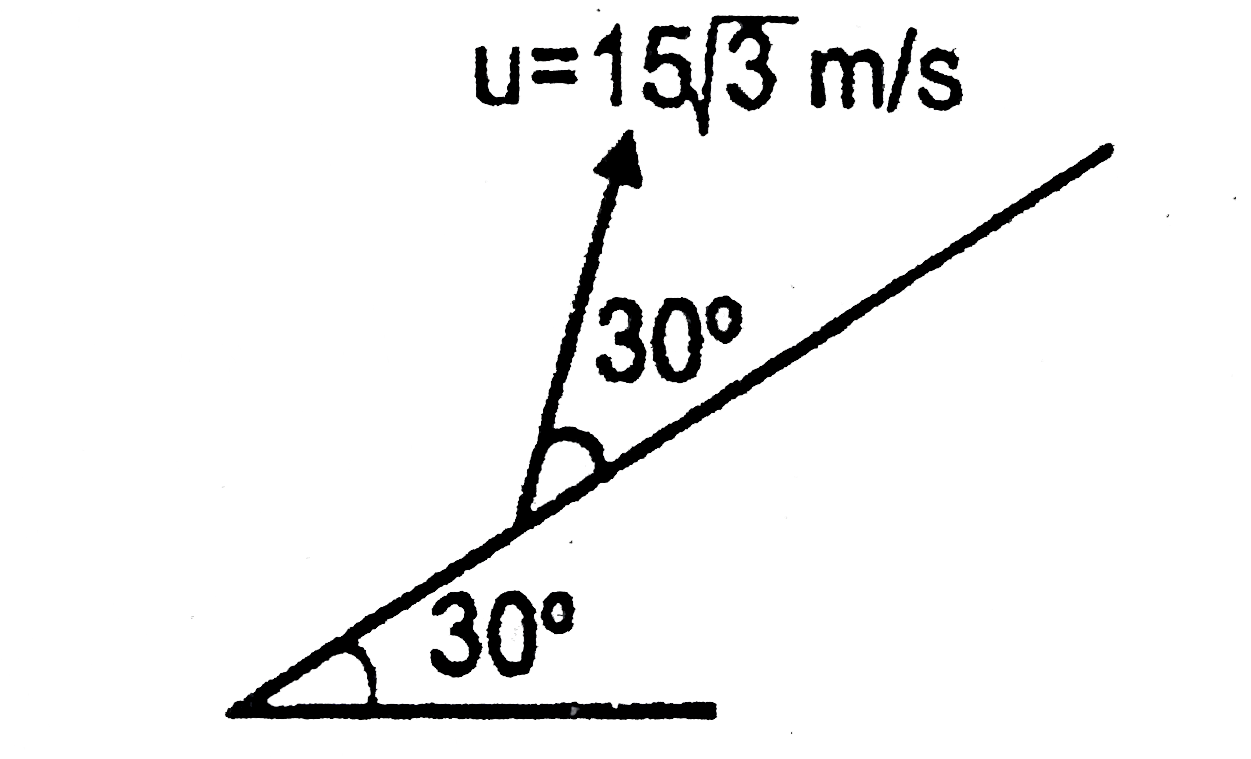
View SolutionA partile is projected up an incline (inclination angle =30∘) with 15√3m/s at an angle of 30∘ with the incline (as shown in figure) (g=10m/s2)
View SolutionA projectile is fired with a velocity v at right angle to the slope inclined at an angle θ with the horizontal. The range of the projectile along the inclined plane is

View SolutionA thin uniform circular ring is rolling down an inclined plane of inclination 30∘ without slipping. Its linear acceleration along the inclined plane will be
View Solution
