Four equal point charges Q each are placed in the xy plane at (0,2), (4,2), (4,-2) and (0, -2). The work required to put a fifth charge Q at the origin of the coordinate system will be
Q24π∈0(1+1√3)
Q24π∈0(1+1√5)
Q22√2π∈0
Q24π∈0
To find the work required to place a fifth charge Q at the origin (0,0) in the presence of four equal point charges Q located at (0,2), (4,2), (4,-2), and (0,-2), we can follow these steps:
Step 1: Calculate the distances from the origin to each charge
The distances from the origin to each of the four charges are as follows:
- Charge at (0,2): Distance = 2
- Charge at (0,-2): Distance = 2
- Charge at (4,2): Distance = √(4−0)2+(2−0)2=√16+4=√20=2√5
- Charge at (4,-2): Distance = √(4−0)2+(−2−0)2=√16+4=√20=2√5
Step 2: Calculate the electric potential at the origin due to each charge
The electric potential V due to a point charge Q at a distance r is given by:
V=kQr
where k=14πϵ0.
Now, we calculate the potential at the origin due to each charge:
- For the charge at (0,2):
V1=kQ2
- For the charge at (0,-2):
V2=kQ2
- For the charge at (4,2):
V3=kQ2√5
- For the charge at (4,-2):
V4=kQ2√5
Step 3: Sum the potentials to find the total potential at the origin
The total potential V at the origin is the sum of the potentials due to all four charges:
V=V1+V2+V3+V4
Substituting the values:
V=kQ2+kQ2+kQ2√5+kQ2√5=kQ(1+1√5)
Step 4: Calculate the work done to bring the fifth charge to the origin
The work W done to bring a charge Q from infinity to a point where the potential is V is given by:
W=Q⋅V
Substituting the expression for V:
W=Q⋅kQ(1+1√5)=kQ2(1+1√5)
Step 5: Substitute k with 14πϵ0
Finally, substituting k:
W=Q24πϵ0(1+1√5)
Final Answer
Thus, the work required to put a fifth charge Q at the origin is:
W=Q24πϵ0(1+1√5)
The distances from the origin to each of the four charges are as follows:
- Charge at (0,2): Distance = 2
- Charge at (0,-2): Distance = 2
- Charge at (4,2): Distance = √(4−0)2+(2−0)2=√16+4=√20=2√5
- Charge at (4,-2): Distance = √(4−0)2+(−2−0)2=√16+4=√20=2√5
The electric potential V due to a point charge Q at a distance r is given by:
V=kQr
where k=14πϵ0.
- For the charge at (0,2):
V1=kQ2
- For the charge at (0,-2):
V2=kQ2
- For the charge at (4,2):
V3=kQ2√5
- For the charge at (4,-2):
V4=kQ2√5
The total potential V at the origin is the sum of the potentials due to all four charges:
V=V1+V2+V3+V4
Substituting the values:
V=kQ2+kQ2+kQ2√5+kQ2√5=kQ(1+1√5)
The work W done to bring a charge Q from infinity to a point where the potential is V is given by:
W=Q⋅V
Substituting the expression for V:
W=Q⋅kQ(1+1√5)=kQ2(1+1√5)
Finally, substituting k:
W=Q24πϵ0(1+1√5)
Thus, the work required to put a fifth charge Q at the origin is:
W=Q24πϵ0(1+1√5)
Topper's Solved these Questions
Similar Questions
Consider two positive point charges, each of magnitude q, placed on the y-axis at the points (0, a) and (0, -a). A positively charged particle of charge q' and mass m is displaced slightly from the origin in the direction of the positive x-axis.
At the origin, charge q' will be in
View SolutionTwo point charges (Q each are placed at (0,y) and (0-y) A point charge q of the same polarity can move along the x-axis. Then
View Solution
Knowledge Check
Four equal charges Q are placed at the four corners of a square of each side is 'a'. Work done in removing a charge −Q from its centre to infinity is
AzeroB√2q2πε0aC√2qπε0aDq2πε0a
Consider two positive point charges, each of magnitude q, placed on the y-axis at the points (0, a) and (0, -a). A positively charged particle of charge q' and mass m is displaced slightly from the origin in the direction of the positive x-axis.
Speed of charge q' at infinity is
View SolutionConsider a system of two equal points charges, each Q=8μC, which are fixed at points (2m, 0 ) and (-2m, 0). Another charge μ is held at a point (0,0.1m) on the y-axis. Mass of the charge μ is 91 mg . At t= 0 , μ is released from rest and it is observed to oscillate along y-axis in a simple harmonic manner. It is also observed that at t = 0 , the force experienced by it is 9×10−3N.
Charge q is
View SolutionTwo point charges of +Q each have been placed at the positions (−a/2,0,0)and(a/2,0,0).The locus of the points where - Q charge can be placed such the that total electrostatic potential energy of the system can become equal to zero, is represented by which of the following equations ?
View SolutionFour charges +q,+q−q, and -q are placed on X - Y plane at the points whose coordinates are (0.5,0),(0,0.5),(−0.5,0)and(0,−0.5) respectively.
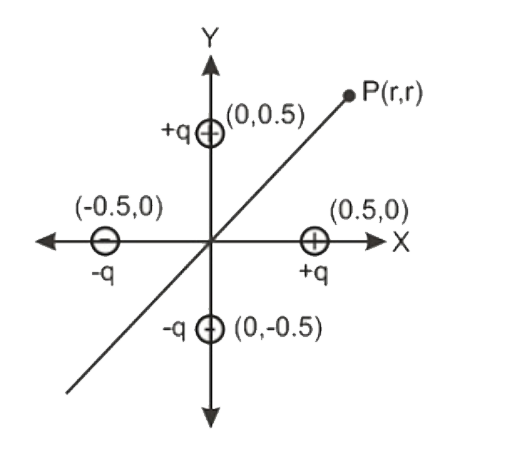
The electric field due to these charges at a point P(r,r), where r>>0.5, will be
View Solution
Consider two point charges q1=q2=q(q>0) placed in x-y plane at (0,−R) and (R,0) as shown in the figure. Now charges q2 starts revolving in anticlockwise sense with uniform angular velocity ω in a circle about origin in xy-plane. E is magnitude of net field at origin, V is potential at origin and Ex is x-component of field at origin then select correct variation of V,Ex and E with time t.
View SolutionTwo point charges 2q and 8q are placed at a distance r apart. Where should a third charge −q be placed between them so that the electrical potential energy of the system is a minimum
View SolutionTwo point charges q each are fixed at (a,0) and (-a,0). A third charge Q is placed at origin. Electrons potential energy of the system will
View Solution
