A particle of mass 220meV/c2 collides with a hydrogen tom at rest. Soon after the collisionthe particle comes to rest, and the atom recoils and goes to its first excited state. The initial kinetic energy of the particle (in eV) is N4. The value of N is :
(Given the mass of the hydrogen atom to be 1GeV/c2)_____________
To solve the problem, we will follow these steps:
Step 1: Identify the masses and their values
- Mass of the particle, m0=220MeV/c2=220×106eV/c2
- Mass of the hydrogen atom, m=1GeV/c2=1×109eV/c2
Step 2: Calculate the ratio of the masses
We need to find the ratio mm0:
mm0=1×109220×106=1092.2×108=102.2≈4.54
Step 3: Apply conservation of momentum
Before the collision, the momentum is given by:
pinitial=m0⋅v
After the collision, the particle comes to rest, and the hydrogen atom recoils with some velocity v1:
pfinal=m⋅v1
By conservation of momentum:
m0⋅v=m⋅v1
Step 4: Express v1 in terms of v
Substituting m=4.54m0:
m0⋅v=4.54m0⋅v1
Cancelling m0 (assuming m0≠0):
v=4.54v1⟹v1=v4.54
Step 5: Calculate the loss in kinetic energy
The initial kinetic energy (KE) of the particle is given as:
KEinitial=12m0v2
The kinetic energy of the hydrogen atom after the collision is:
KEfinal=12mv21=12(4.54m0)(v4.54)2=12(4.54m0)(v220.6596)
Thus, the total kinetic energy after collision becomes:
KEfinal=4.542⋅20.6596m0v2
Step 6: Set up the energy conservation equation
The loss in kinetic energy is equal to the gain in energy of the hydrogen atom, which is given as 10.2eV:
KEinitial−KEfinal=10.2
Substituting the expressions:
12m0v2−4.542⋅20.6596m0v2=10.2
Factoring out 12m0v2:
12m0v2(1−4.5420.6596)=10.2
Step 7: Solve for v2
Calculating 4.5420.6596≈0.219:
12m0v2(1−0.219)=10.2⟹12m0v2(0.781)=10.2
m0v2=10.2×20.781≈26.1
Step 8: Relate to initial kinetic energy
The initial kinetic energy is given as N4:
KEinitial=12m0v2=N4
Thus,
N4=12m0v2≈26.12⟹N≈52.2
Rounding gives N=51.
Final Answer
The value of N is 51.
---
- Mass of the particle, m0=220MeV/c2=220×106eV/c2
- Mass of the hydrogen atom, m=1GeV/c2=1×109eV/c2
We need to find the ratio mm0:
mm0=1×109220×106=1092.2×108=102.2≈4.54
Before the collision, the momentum is given by:
pinitial=m0⋅v
After the collision, the particle comes to rest, and the hydrogen atom recoils with some velocity v1:
pfinal=m⋅v1
By conservation of momentum:
m0⋅v=m⋅v1
Substituting m=4.54m0:
m0⋅v=4.54m0⋅v1
Cancelling m0 (assuming m0≠0):
v=4.54v1⟹v1=v4.54
The initial kinetic energy (KE) of the particle is given as:
KEinitial=12m0v2
The kinetic energy of the hydrogen atom after the collision is:
KEfinal=12mv21=12(4.54m0)(v4.54)2=12(4.54m0)(v220.6596)
Thus, the total kinetic energy after collision becomes:
KEfinal=4.542⋅20.6596m0v2
The loss in kinetic energy is equal to the gain in energy of the hydrogen atom, which is given as 10.2eV:
KEinitial−KEfinal=10.2
Substituting the expressions:
12m0v2−4.542⋅20.6596m0v2=10.2
Factoring out 12m0v2:
12m0v2(1−4.5420.6596)=10.2
Calculating 4.5420.6596≈0.219:
12m0v2(1−0.219)=10.2⟹12m0v2(0.781)=10.2
m0v2=10.2×20.781≈26.1
The initial kinetic energy is given as N4:
KEinitial=12m0v2=N4
Thus,
N4=12m0v2≈26.12⟹N≈52.2
Rounding gives N=51.
The value of N is 51.
Topper's Solved these Questions
Similar Questions
A particle of mass m is moving along the x-axis with initial velocity ui . It collides elastically with a particle of mass 10 m at rest and then moves with half its initial kinetic energy (see figure).If sinθ1=√nsinθ2 then value of n is
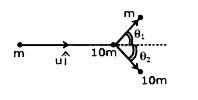
View SolutionA particle of mass m with an initial velocity uˆi+2uˆj collides with a particle of mass 3m at rest. After collision, the two particles stick together and the combined particle moves with a velocity vˆi+v'ˆj. Which of the following is incorrect?
View SolutionA nucleus of mass 220 amu in the free state decays to emit an α-particle . Kinetic energy of the α-particle emitted is 5.4 MeV. The recoil energy of the daughter nucleus is
View SolutionA particle of mass m1 makes a head - on elastic collision with another particle of mass m2 at rest. m1 rebounds straight back with 49 of its initial kinetic energy . Then m1m2 is :
View SolutionConsider a hydrogen atom with its electron in the nth orbital An electomagnetic radiation of wavelength 90nm is used to ionize the atom . If the kinetic energy of the ejected electron is 10.4eV , then the value of n is ( hc = 1242 eVnm)
View SolutionAn electron collides with a hydrogen atom in its ground state and excites it to n=3 ,. The energy gives to hydrogen aton n this inclastic collision is [Neglect the recoiling of hydrogen atom]
View SolutionAn electron collides with a hydrogen atom in its ground state and excites it to n=3 ,. The energy gives to hydrogen aton n this inclastic collision is [Neglect the recoiling of hydrogen atom]
View SolutionThe energy of a hydrogen atom in its ground state is −13.6eV. The energy of the level corresponding to the quantum number n=2 (first excited state) in the hydrogen atom is
View SolutionA neutron having kinetic energy 12.5eV collides with a hydrogen atom at rest negect the difference in mass between the neutron and the hydrogen atom and assume that the neutron does not leave its of motion find the posible kinetic energy of the neutron after the event
View SolutionA particle of mass m moving with speed u collides perfectly inelastically with another particle of mass 2m at rest. Find loss of kinetic energy of system in the collision.
View Solution
