Two capacitors having capacitances and are charged with 120 V and 200 V batteries respectively. When they are connected in parallel now, it is found that the potential on each one of them is zero. Then,
The correct Answer is:A
To solve the problem, we need to analyze the situation with the two capacitors charged to different voltages and then connected in parallel. Here’s a step-by-step solution:
Step 1: Understand the initial conditions
We have two capacitors, C1 and C2, charged to 120 V and 200 V, respectively. When connected in parallel, we need to find out under what conditions the potential across both capacitors becomes zero.
Hint: Consider how the charges on the capacitors behave when connected in parallel.
Step 2: Calculate the charges on each capacitor
The charge on a capacitor is given by the formula:
Q=C×V
For capacitor C1:
Q1=C1×120
For capacitor C2:
Q2=C2×200
Hint: Remember that the charge is dependent on both the capacitance and the voltage.
Step 3: Analyze the connection of the capacitors
When the capacitors are connected in parallel, if we connect them with opposite polarities (the positive terminal of one to the negative terminal of the other), the charges will oppose each other. For the potential across both capacitors to be zero, the total charge must also be zero:
Q1−Q2=0
This implies:
Q1=Q2
Hint: Think about how opposing charges can cancel each other out.
Step 4: Set up the equation
From the previous step, we have:
C1×120=C2×200
Hint: This equation relates the charges based on the capacitances and voltages.
Step 5: Rearrange the equation
Rearranging the equation gives us:
120C1=200C2
Dividing both sides by 40:
3C1=5C2
Hint: Simplifying the equation can help you find a relationship between the two capacitances.
Step 6: Conclusion
The relationship between the capacitances of the two capacitors is:
C1C2=53
Thus, the answer is that the ratio of the capacitances C1 and C2 is 53.
---
We have two capacitors, C1 and C2, charged to 120 V and 200 V, respectively. When connected in parallel, we need to find out under what conditions the potential across both capacitors becomes zero.
The charge on a capacitor is given by the formula:
Q=C×V
For capacitor C1:
Q1=C1×120
For capacitor C2:
Q2=C2×200
When the capacitors are connected in parallel, if we connect them with opposite polarities (the positive terminal of one to the negative terminal of the other), the charges will oppose each other. For the potential across both capacitors to be zero, the total charge must also be zero:
Q1−Q2=0
This implies:
Q1=Q2
From the previous step, we have:
C1×120=C2×200
Rearranging the equation gives us:
120C1=200C2
Dividing both sides by 40:
3C1=5C2
The relationship between the capacitances of the two capacitors is:
C1C2=53
Topper's Solved these Questions
Similar Questions
Two capacitors with capacities C1 and C2 ,are charged to potentials V1 and V2 respectively.When they are connected in parallel,the ratio of their respective charges is ....?
View SolutionTwo capacitors C1 and C2 are charged to 120V and 200V respectively. It is found that connecting them together the potential on each one can be made zero. Then
View SolutionTwo capacitors with capacitances C1andC2 are connected in parallel. Find the resultant capacitance.
View SolutionTwo capacitors of 10pF and 20pF are connected to 200 V and 100 V sources, respectively. If they are connected by the wire, then what is the common potential of the capacitors?
View SolutionTwo capacitors of capacitance 2μF and 3μF respectively are charged to potential difference 20 V and 40 V respectively. Now the capacitors are connected in series with a resistance such that the positively charged plate of one capacitor is connected to the positively charged plate of the other. The initial current through the resistance is I0. The potential difference across the 2μF capacitor at the instant the current has reduced to I02 is_______ V.
View SolutionTwo capacitors of capacitance C and 3C are charged to potential difference V0 and 2V0, respectively, and connected to an inductor of inductance L as shows in Fig. Initially, the current in the inductor is zero. Now, switch S is closed.

Potential difference across capacitor of capacitance C when the current in the circuit is maximum is
View SolutionTwo capacitors of capacitance C and 3C are charged to potential difference V0 and 2V0, respectively, and connected to an inductor of inductance L as shows in Fig. Initially, the current in the inductor is zero. Now, switch S is closed.

Potential difference across capacitor of capacitance 3C when the current in the circuit is maximum is
View SolutionTwo capacitors of capacitance C and 3C are charged to potential difference V0 and 2V0, respectively, and connected to an inductor of inductance L as shows in Fig. Initially, the current in the inductor is zero. Now, switch S is closed.
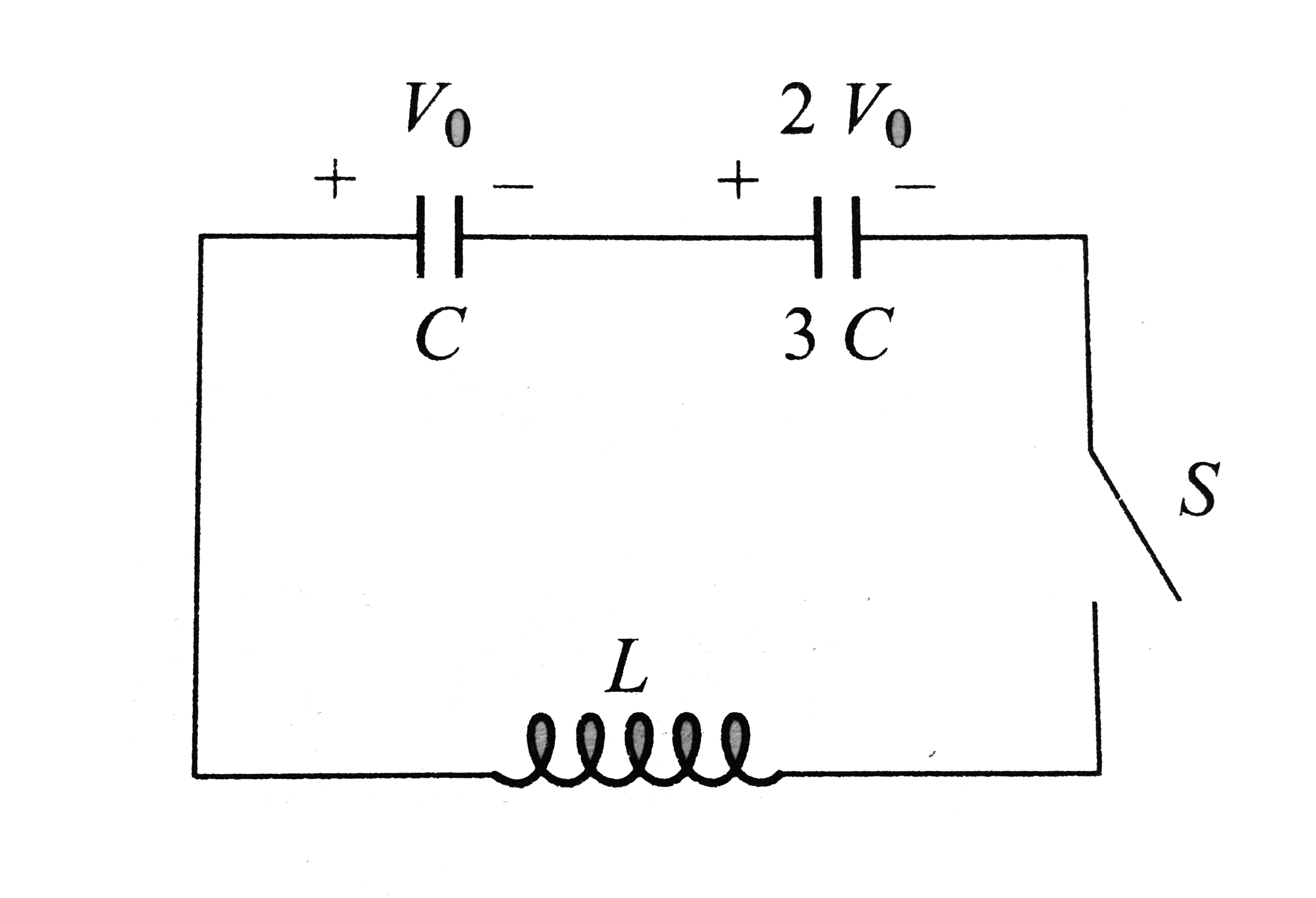
The maximum current in the inductor is
View SolutionThree capacitors of capacitance C1=3μf,C2=6μfandC3=10μf, are connected to a 10V battery as shown in Figure 3 below
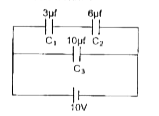
Calculate:
Equivalent capacitance
View SolutionTwo capacitors of capacitances 3μF and 6μF are charged to a potential of 12V each. They are now connected to each other, with the positive plate of each joined to the negative plate of the other. The potential difference across each will be
View Solution
