A hoop of radius r mass m rotating with an angular velocity ω0 is placed on a rough horizontal surface. The initial velocity of the centre of the hoop is zero. What will be the velocity of the centre of the hoop when it cases to slip ?
rω03
rω02
rω0
rω04
The correct Answer is:B
To solve the problem, we need to analyze the motion of the hoop as it transitions from slipping to rolling without slipping. Here’s the step-by-step solution:
Step 1: Understand the Initial Conditions
The hoop has a radius r and mass m. It is initially rotating with an angular velocity ω0 and has a center of mass velocity of 0.
Step 2: Determine the Velocity of the Contact Point
The point of contact with the ground (let's call it point B) has a velocity due to the rotation of the hoop. The velocity of point B is given by:
vB=ω0⋅r
Since the hoop is initially at rest in terms of translational motion, this point is moving backward relative to the ground.
Step 3: Analyze the Effect of Friction
As the hoop rotates, the frictional force acts at point B in the forward direction (to the right). This friction will reduce the angular velocity ω0 and create a linear velocity v in the forward direction.
Step 4: Set Up the Condition for Rolling Without Slipping
For the hoop to cease slipping, the velocity of the center of mass v must equal the velocity of the point of contact B when it is at rest (which is zero). The net velocity of point A (the center of the hoop) can be expressed as:
vA=v−ωr
Setting this equal to zero for rolling without slipping gives:
v−ωr=0⇒v=ωr
Step 5: Apply Conservation of Angular Momentum
The torque about point B is zero (since it is the point of contact), which means angular momentum is conserved about this point. The initial angular momentum Li is:
Li=I⋅ω0=mr2⋅ω0
where I is the moment of inertia of the hoop about its center.
The final angular momentum Lf when the hoop is rolling without slipping is:
Lf=I⋅ω+mvr=mr2⋅ω+mvr
Step 6: Set Initial and Final Angular Momentum Equal
Setting Li=Lf:
mr2⋅ω0=mr2⋅ω+mvr
Canceling m from both sides:
r2⋅ω0=r2⋅ω+vr
Step 7: Substitute v=ωr
Substituting v=ωr into the equation gives:
r2⋅ω0=r2⋅ω+ωr2
This simplifies to:
r2⋅ω0=r2⋅ω+r2⋅ω
r2⋅ω0=2r2⋅ω
Step 8: Solve for v
Dividing both sides by 2r2 gives:
ω=ω02
Substituting back to find v:
v=ωr=ω02⋅r
Final Result
Thus, the velocity of the center of the hoop when it ceases to slip is:
v=ω0r2
The hoop has a radius r and mass m. It is initially rotating with an angular velocity ω0 and has a center of mass velocity of 0.
The point of contact with the ground (let's call it point B) has a velocity due to the rotation of the hoop. The velocity of point B is given by:
vB=ω0⋅r
Since the hoop is initially at rest in terms of translational motion, this point is moving backward relative to the ground.
As the hoop rotates, the frictional force acts at point B in the forward direction (to the right). This friction will reduce the angular velocity ω0 and create a linear velocity v in the forward direction.
For the hoop to cease slipping, the velocity of the center of mass v must equal the velocity of the point of contact B when it is at rest (which is zero). The net velocity of point A (the center of the hoop) can be expressed as:
vA=v−ωr
Setting this equal to zero for rolling without slipping gives:
v−ωr=0⇒v=ωr
The torque about point B is zero (since it is the point of contact), which means angular momentum is conserved about this point. The initial angular momentum Li is:
Li=I⋅ω0=mr2⋅ω0
where I is the moment of inertia of the hoop about its center.
Lf=I⋅ω+mvr=mr2⋅ω+mvr
Setting Li=Lf:
mr2⋅ω0=mr2⋅ω+mvr
Canceling m from both sides:
r2⋅ω0=r2⋅ω+vr
Substituting v=ωr into the equation gives:
r2⋅ω0=r2⋅ω+ωr2
This simplifies to:
r2⋅ω0=r2⋅ω+r2⋅ω
r2⋅ω0=2r2⋅ω
Dividing both sides by 2r2 gives:
ω=ω02
Substituting back to find v:
v=ωr=ω02⋅r
Thus, the velocity of the center of the hoop when it ceases to slip is:
v=ω0r2
Topper's Solved these Questions
Similar Questions
A solid sphere is thrown on a horizontal rough surface with initial velocity of centre of mass V0 without rolling. Velocity of its centre of mass when its starts pure rolling is
View SolutionA disc is given an initial angular velocity ω0 and placed on a rough horizontal surface as shown Fig. The quantities which will not depend on the coefficient of friction is/are

View SolutionA disc of mass m and radius R rotating with angular speed ω0 is placed on a rough surface (co-officient of friction =μ). Then

View SolutionA uniform ring of radius R is given a back spin of angular velocity V0/2R and thrown on a horizontal rough surface with velocity of centre to be V0. The velocity of the centre of the ring when it starts pure rolling will be
View SolutionA ring of radius R is first rotated with an angular velocity ω and then carefully placed on a rough horizontal surface. The coefficient of friction between the surface and the ring is μ. Time after which its angular speed is reduced to half is
View SolutionA conducting ring of radius r having charge q is rotating with angular velocity ω about its axes. Find the magnetic field at the centre of the ring.

View SolutionA conducting ring of radius r having charge q is rotating with angular velocity ω about its axes. Find the magnetic field at the centre of the ring.

View SolutionA horizontal disk is rotating with angular velocity ω about a vertical axis passing through its centre. A ball is placed at the centre of groove and pushed slightly. The velocity of the ball when it comes out of the groove -

View SolutionA ring of radius 'r' and mass per unit length 'm' rotates with an angular velocity 'ω' in free space then tension will be :
View SolutionA cycle tyre of mass M and radius R is in pure rolling over a horizontal surface. If the velocity of the centre of mass of the tyre is v, then the velocity of point P on the tyre, shown in figure is
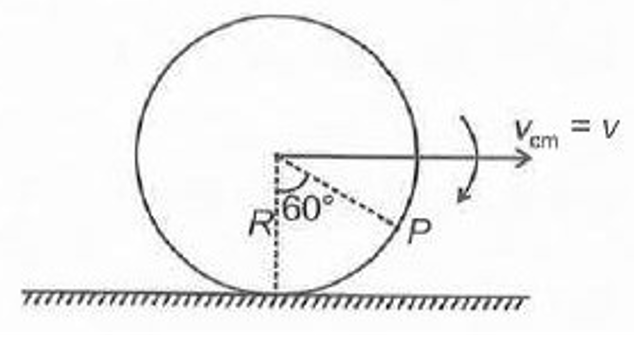
View Solution
