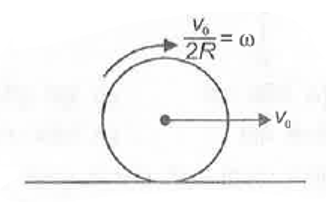
A uniform ring of radius R is given a back spin of angular velocity V0/2R and thrown on a horizontal rough surface with velocity of centre to be V0. The velocity of the centre of the ring when it starts pure rolling will be
V02
V04
3V04
0
The correct Answer is:B
To solve the problem, we need to analyze the motion of the uniform ring as it transitions from sliding to pure rolling. Here are the steps to find the velocity of the center of the ring when it starts pure rolling:
Step 1: Understand the Initial Conditions
- The ring has a radius R.
- It is given a backspin with an angular velocity ω0=V02R.
- The initial velocity of the center of the ring is V0.
Step 2: Define the Final Conditions
- Let the final velocity of the center of the ring be V.
- Let the final angular velocity when the ring starts pure rolling be ω.
Step 3: Apply the Condition for Pure Rolling
For pure rolling, the relationship between the linear velocity V and the angular velocity ω is given by:
V=Rω
Step 4: Conservation of Angular Momentum
We will consider the angular momentum about the point of contact with the ground. The initial angular momentum Li is given by:
Li=Icmω0+mV0R
where Icm for a ring is mR2. Thus,
Li=mR2(−V02R)+mV0R=−mV0R2+mV0R=mV0R2
Step 5: Final Angular Momentum
The final angular momentum Lf when the ring is rolling without slipping is:
Lf=Icmω+mVR
Substituting Icm=mR2 and V=Rω:
Lf=mR2ω+mVR=mR2ω+mR2ω=2mR2ω
Step 6: Set Initial and Final Angular Momentum Equal
Since no external torques act on the system, we have:
Li=Lf
Thus,
mV0R2=2mR2ω
Canceling m and R (assuming R≠0):
V02=2Rω⟹ω=V04R
Step 7: Substitute Back to Find V
Using the relationship V=Rω:
V=R(V04R)=V04
Conclusion
The velocity of the center of the ring when it starts pure rolling is:
V04
- The ring has a radius R.
- It is given a backspin with an angular velocity ω0=V02R.
- The initial velocity of the center of the ring is V0.
- Let the final velocity of the center of the ring be V.
- Let the final angular velocity when the ring starts pure rolling be ω.
For pure rolling, the relationship between the linear velocity V and the angular velocity ω is given by:
V=Rω
We will consider the angular momentum about the point of contact with the ground. The initial angular momentum Li is given by:
Li=Icmω0+mV0R
where Icm for a ring is mR2. Thus,
Li=mR2(−V02R)+mV0R=−mV0R2+mV0R=mV0R2
The final angular momentum Lf when the ring is rolling without slipping is:
Lf=Icmω+mVR
Substituting Icm=mR2 and V=Rω:
Lf=mR2ω+mVR=mR2ω+mR2ω=2mR2ω
Since no external torques act on the system, we have:
Li=Lf
Thus,
mV0R2=2mR2ω
Canceling m and R (assuming R≠0):
V02=2Rω⟹ω=V04R
Using the relationship V=Rω:
V=R(V04R)=V04
The velocity of the center of the ring when it starts pure rolling is:
V04
Topper's Solved these Questions
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - RIGID BODY DYNAMICS 2EXERCISE - Multiple Correct26videos
RIGID BODY DYNAMICS 2
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - RIGID BODY DYNAMICS 2EXERCISE - Linked Comprehension71videos
RIGID BODY DYNAMICS 2
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - RIGID BODY DYNAMICS 2EXERCISE - Subjective19videos
RIGID BODY DYNAMICS 2
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - RIGID BODY DYNAMICS 1EXERCISE - Integer11videos
RIGID BODY DYNAMICS 1
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - SOUND WAVES AND DOPPLER EFFECTEXERCISE - Integer16videos
SOUND WAVES AND DOPPLER EFFECT
Similar Questions
A solid sphere is thrown on a horizontal rough surface with initial velocity of centre of mass V0 without rolling. Velocity of its centre of mass when its starts pure rolling is
View SolutionA hoop of radius r mass m rotating with an angular velocity ω0 is placed on a rough horizontal surface. The initial velocity of the centre of the hoop is zero. What will be the velocity of the centre of the hoop when it cases to slip ?
View SolutionA heavy solid sphere is thrown on a horizontal rough surface with initial velocity u without rolling. What will be its speed, when it starts pure rolling motion ?
View SolutionA uniform ring of mass m and radius R is performing pure rolling motion on a horizontal surface. The velocity of centre of the ring is V0. If at the given instant the kinetic energy of the semi circular are AOB is lambda mv0_(2), then find the value of 11λ(takeπ=227)
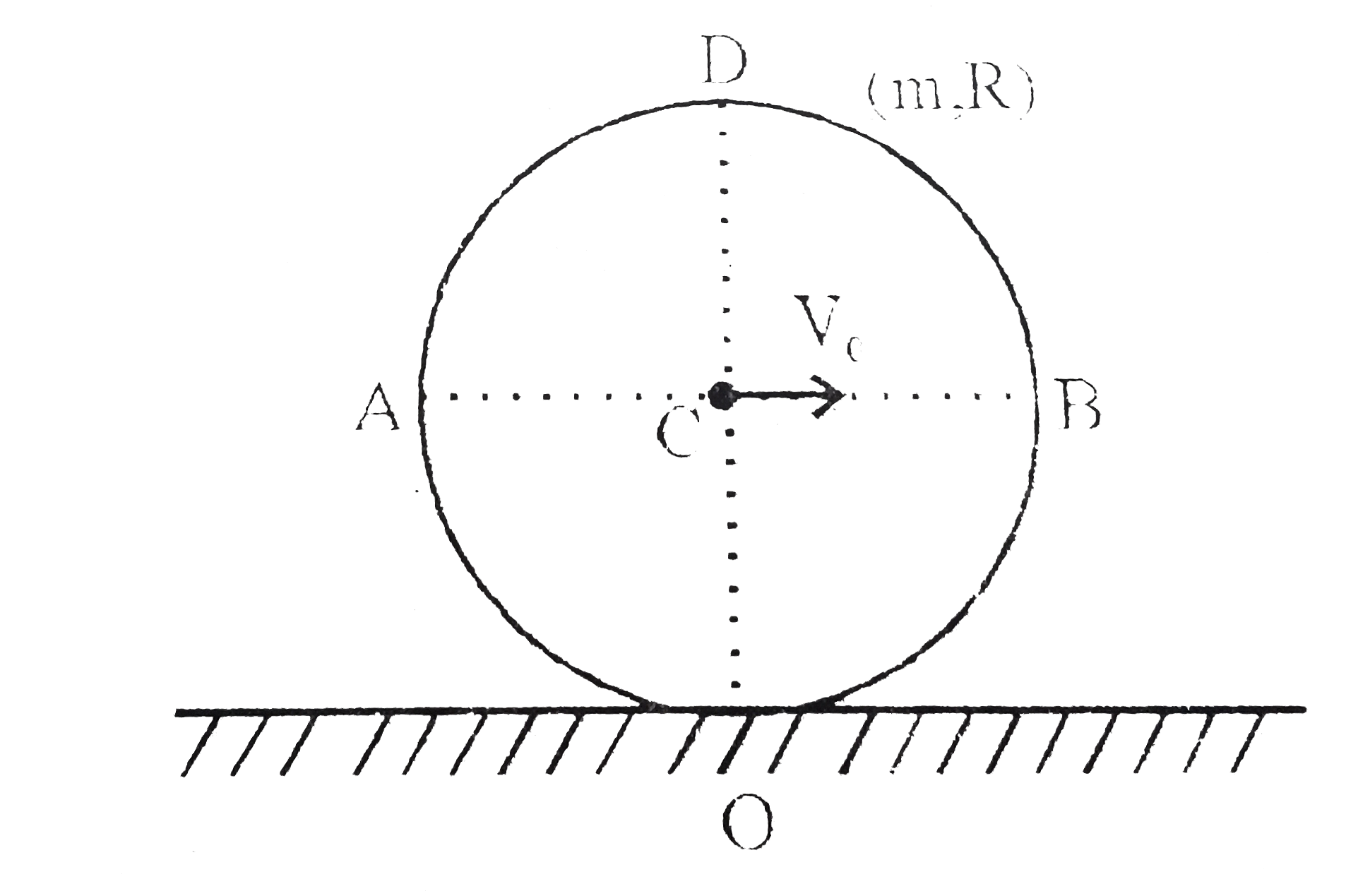 View Solution
View SolutionA uniform ring of mass m and radius R is performing pure rolling motion on a horizontal surface. The velocity of centre of the ring is V0. If at the given instant the kinetic energy of the semi circular are AOB is lambda mv0_(2), then find the value of 11λ(takeπ=227)
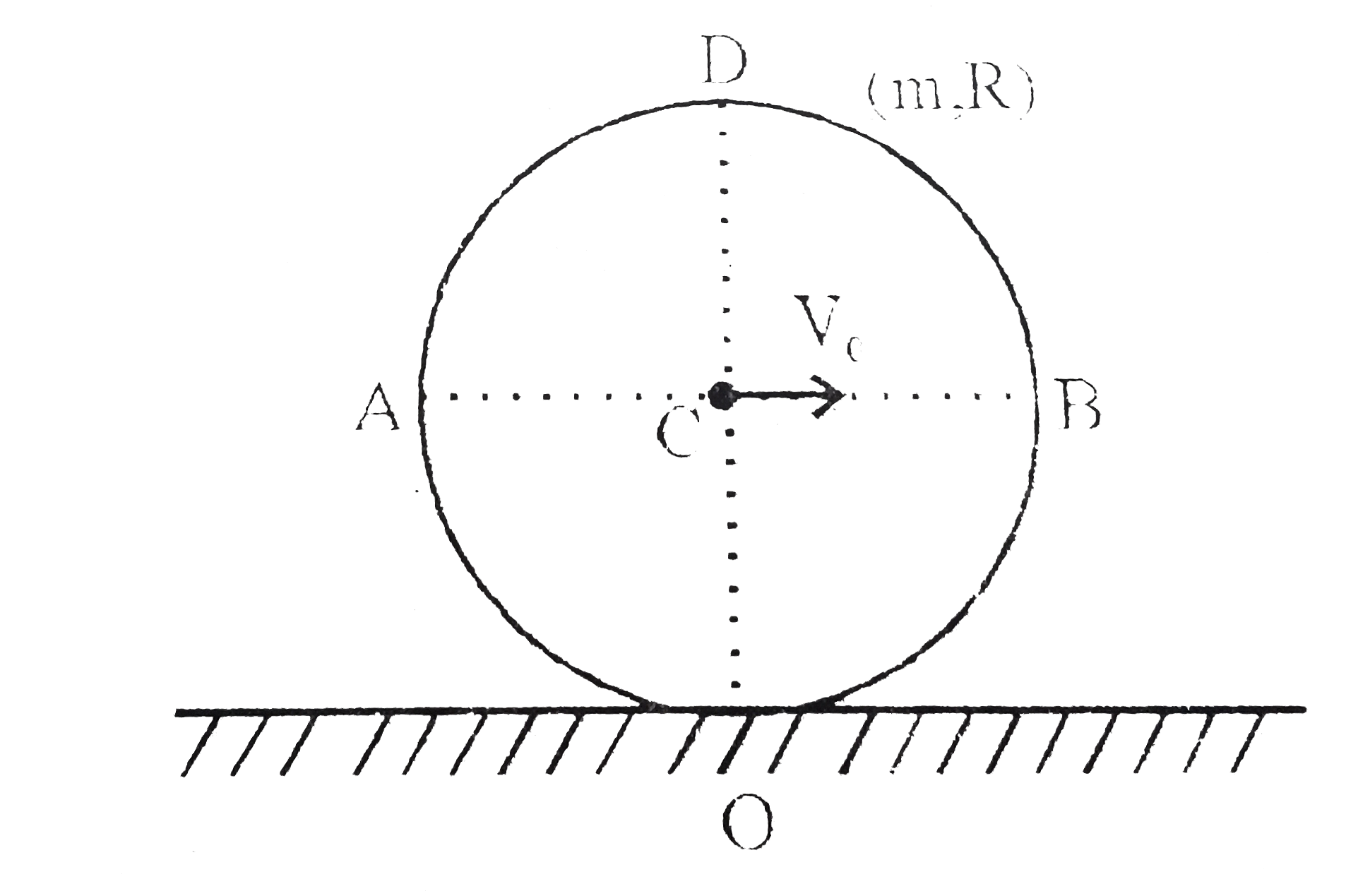 View Solution
View SolutionA thin ring of mass m and radius R is in pure rolling over a horizontal surface. If v0 is the velocity of the centre of mass of the ring, then the angular momentum of the ring about the point of contact is
View SolutionA cylinder of mass m and radius R is kept on a rough surface after giving its centre a horizontal speed v0. Find the speed of the centre of the cylinder when it stops slipping.
View SolutionA cycle tyre of mass M and radius R is in pure rolling over a horizontal surface. If the velocity of the centre of mass of the tyre is v, then the velocity of point P on the tyre, shown in figure is
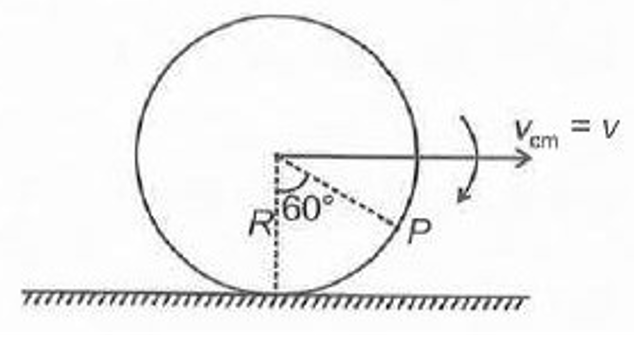 View Solution
View SolutionA solid sphere has combined linear and rotation motion as shown in figure. The velocity of its centre of mass when it starts pure rolling is (R = radius of sphere)
 View Solution
View SolutionA solid sphere has combined linear and rotation motion as shown in figure. The velocity of its centre of mass when it starts pure rolling is (R = radius of sphere)
View Solution

