A disc rotates about its aixs of symmetry in a horizontal plane at a steady rate of 3.5 revolutions per second A coin placed at a distance fo 1.25 cm form the axis of ratation remains at rest on the disc The coefficient of friction between the coin and the disc is : (g=10/s2)
0.6
0.5
0.7
0.3
To solve the problem, we need to determine the coefficient of friction (μ) between the coin and the disc based on the given parameters. Here's the step-by-step solution:
Step 1: Understand the Forces Involved
The coin remains at rest on the disc due to the frictional force providing the necessary centripetal force to keep it moving in a circular path. The centripetal force (F_c) required for circular motion is provided by the frictional force (F_f).
Step 2: Write the Expression for Centripetal Force
The centripetal force can be expressed as:
Fc=m⋅ω2⋅r
where:
- m = mass of the coin
- ω = angular velocity in radians per second
- r = distance from the axis of rotation (1.25 cm = 0.0125 m)
Step 3: Maximum Frictional Force
The maximum frictional force can be expressed as:
Ffmax=μ⋅m⋅g
where:
- g = acceleration due to gravity (10 m/s²)
Step 4: Set Up the Equation
Since the coin is at rest, the frictional force must equal the centripetal force:
m⋅ω2⋅r≤μ⋅m⋅g
Step 5: Cancel the Mass
We can cancel the mass m from both sides (assuming m≠0):
ω2⋅r≤μ⋅g
Step 6: Solve for the Coefficient of Friction
Rearranging gives us:
μ≥ω2⋅rg
Step 7: Calculate the Angular Velocity
The angular velocity ω is given in revolutions per second. We need to convert it to radians per second:
ω=3.5rev/s×2πrad/rev=7πrad/s
Step 8: Substitute Values
Now we can substitute ω, r, and g into the equation:
- ω=7πrad/s
- r=0.0125m
- g=10m/s2
Calculating ω2⋅r:
ω2=(7π)2=49π2
ω2⋅r=49π2⋅0.0125
Step 9: Calculate μ
Now substituting into the inequality:
μ≥49π2⋅0.012510
Calculating the numerical value:
μ≥49⋅9.87⋅0.012510≈6.042510≈0.60425
Final Result
Thus, the coefficient of friction μ is approximately:
μ≈0.6
Summary
The coefficient of friction between the coin and the disc is μ≈0.6.
---
The coin remains at rest on the disc due to the frictional force providing the necessary centripetal force to keep it moving in a circular path. The centripetal force (F_c) required for circular motion is provided by the frictional force (F_f).
The centripetal force can be expressed as:
Fc=m⋅ω2⋅r
where:
- m = mass of the coin
- ω = angular velocity in radians per second
- r = distance from the axis of rotation (1.25 cm = 0.0125 m)
The maximum frictional force can be expressed as:
Ffmax=μ⋅m⋅g
where:
- g = acceleration due to gravity (10 m/s²)
Since the coin is at rest, the frictional force must equal the centripetal force:
m⋅ω2⋅r≤μ⋅m⋅g
We can cancel the mass m from both sides (assuming m≠0):
ω2⋅r≤μ⋅g
Rearranging gives us:
μ≥ω2⋅rg
The angular velocity ω is given in revolutions per second. We need to convert it to radians per second:
ω=3.5rev/s×2πrad/rev=7πrad/s
Now we can substitute ω, r, and g into the equation:
- ω=7πrad/s
- r=0.0125m
- g=10m/s2
ω2=(7π)2=49π2
ω2⋅r=49π2⋅0.0125
Now substituting into the inequality:
μ≥49π2⋅0.012510
μ≥49⋅9.87⋅0.012510≈6.042510≈0.60425
Thus, the coefficient of friction μ is approximately:
μ≈0.6
The coefficient of friction between the coin and the disc is μ≈0.6.
Topper's Solved these Questions
Similar Questions
A horizontal turn table rotates about its axis at the uniform rate of 2revolutions per second. Find the maximum distance from the axis at which a small body will remain stationary on the turn table if the coefficient of static friction between the turn table and body is 0.8. Assume g=π2m/s2.
View SolutionA boy is sitting on the horizontal platform of a joy wheel at a distance of 5 m from the center. The wheel begins to rotate and when angular speed exceeds 1 rad/s, the boy just slips. The coefficient of friction between the boy and the wheel is (g=10m/s2)
View Solution
Knowledge Check
A disc revovles with a speed of 3313rev/min and has a radius of 15 cm Two coins are palaced at 4 cm and 14 cm away from the center of the record If the coefficient of friction between the coins and the record is 0.5 which of the coins will revolve with the road ?
AABBCBoth A and BDNeither A nor B
A circular disc is made to rotate in horizontal plane about its centre at the rate of 2 rps. The greatest distance of a coin placed on the disc from its centre so that it does not skid is (μ is coefficient of friction)
View SolutionA disc rotates about its axis with a constant angular acceleration of 4rads2. Find the radial and tangential acceleration of a particle at a distance of 1 cm from the axis at the end of the first second after the disc starts rotating.
View SolutionA block A of mass 2 kg rests on a horizontal surface. Another block B of mass 1 kg moving at a speed of m/s when at a distance of 16 cm from A. collides elastically with A. The coefficeint of friction between the horizontal surface and earth of the blocks is 0.2. Then (g=10m/s2)
View SolutionA uniform disc of mass m and radius R is rotated about an axis passing through its center and perpendicular to its plane with an angular velocity ω. It is placed on a rough horizontal plane with the axis of the disc keeping vertical. Coefficient of friction between the disc and the surface is μ, find
(a). The time when disc stops rotating
(b). The angle rotated by the disc before stopping.
View SolutionA car starts from rest at time t = 0 and it a-t graph is shown in figure. A coin is initially at rest on the floor of the car. At t = 1 s the coin begins to slip and it stops slipping at t = 3 s. The coefficient of static friction between the floor and the coin is (g = 10 m/s2)
_PHY_E05_188_Q02.png)
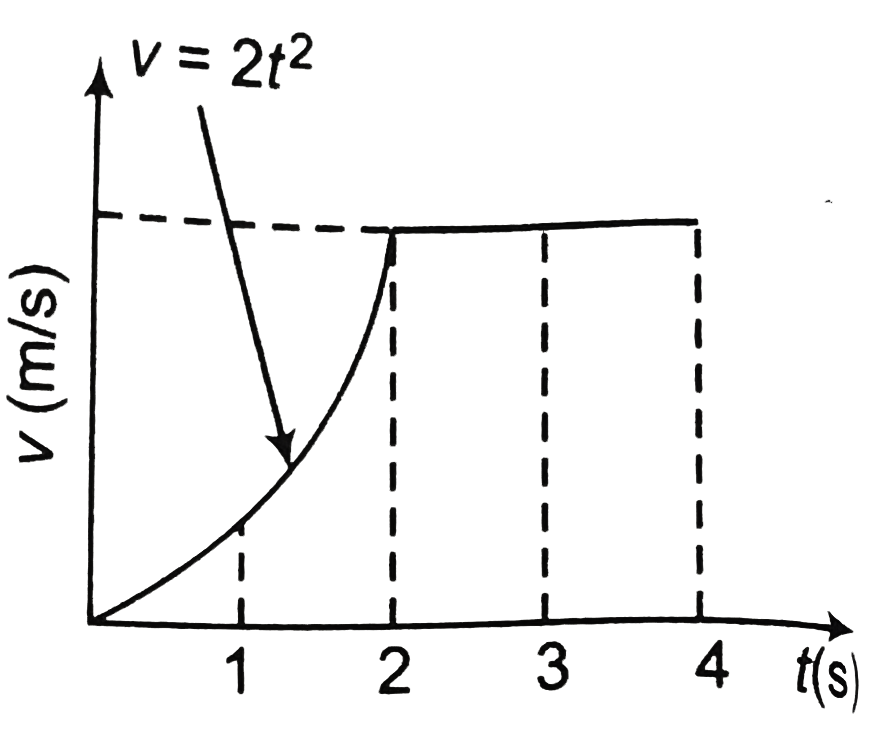
View SolutionA car begains from rest at time t=0, and then acceleration along a straight track during the interval 0<t≤2s and thereafter with constant velocity as shown in figure in the graph. A coin is initially at rest on the floor of the car. At t=1s, the coin begains to slip and its stops slipping at t=3s . The coefficient of static friction between the floor and the coin is (g=10m/s2)
View SolutionA disc starts rotating with a constant angular acceleration of 1rad/s2 about a fixed vertical axis perpendicular to its plane and passing through its centre. A coin of mass 10gm is placed on the disc at a distance of 10cm from the axis. The coefficent of friction between the disc and the coin is 0.2. The value of the frictional force on the coin at t=1s will be
View Solution
