A boy is sitting on the horizontal platform of a joy wheel at a distance of 5 m from the center. The wheel begins to rotate and when angular speed exceeds 1 rad/s, the boy just slips. The coefficient of friction between the boy and the wheel is (g=10m/s2)
0.5
0.32
0.71
0.2
To solve the problem step by step, we will analyze the forces acting on the boy and apply the concepts of circular motion and friction.
1. Identify the Forces:
- The boy experiences a centrifugal force due to the rotation of the wheel, which can be expressed as:
Fcentrifugal=mω2r
- The frictional force acting on the boy, which prevents him from slipping, is given by:
Ffriction=μN
- Here, N is the normal force, which equals the gravitational force acting on the boy, mg.
2. Set Up the Equation:
- When the boy is on the verge of slipping, the frictional force equals the centrifugal force:
μN=mω2r
- Since N=mg, we can substitute this into the equation:
μmg=mω2r
3. Simplify the Equation:
- We can cancel the mass m from both sides (assuming m≠0):
μg=ω2r
4. Substitute Known Values:
- Given:
- g=10m/s2
- ω=1rad/s
- r=5m
- Substitute these values into the equation:
μ⋅10=(1)2⋅5
5. Calculate the Coefficient of Friction:
- Simplifying the equation:
μ⋅10=5
- Therefore, solving for μ:
μ=510=0.5
Final Answer:
The coefficient of friction between the boy and the wheel is μ=0.5.
---
- The boy experiences a centrifugal force due to the rotation of the wheel, which can be expressed as:
Fcentrifugal=mω2r
- The frictional force acting on the boy, which prevents him from slipping, is given by:
Ffriction=μN
- Here, N is the normal force, which equals the gravitational force acting on the boy, mg.
- When the boy is on the verge of slipping, the frictional force equals the centrifugal force:
μN=mω2r
- Since N=mg, we can substitute this into the equation:
μmg=mω2r
- We can cancel the mass m from both sides (assuming m≠0):
μg=ω2r
- Given:
- g=10m/s2
- ω=1rad/s
- r=5m
- Substitute these values into the equation:
μ⋅10=(1)2⋅5
- Simplifying the equation:
μ⋅10=5
- Therefore, solving for μ:
μ=510=0.5
The coefficient of friction between the boy and the wheel is μ=0.5.
Topper's Solved these Questions
- LAWS OF MOTIONBOOK - AAKASH INSTITUTE ENGLISHCHAPTER - LAWS OF MOTIONEXERCISE - Assignment (SECTION-B)
44 Videos
- LAWS OF MOTIONBOOK - AAKASH INSTITUTE ENGLISHCHAPTER - LAWS OF MOTIONEXERCISE - Assignment (SECTION-C)
63 Videos
- LAWS OF MOTIONBOOK - AAKASH INSTITUTE ENGLISHCHAPTER - LAWS OF MOTIONEXERCISE - EXERCISE
69 Videos
- KINETIC THEORYBOOK - AAKASH INSTITUTE ENGLISHCHAPTER - KINETIC THEORYEXERCISE - EXERCISE (ASSIGNMENT) SECTION - D Assertion - Reason Type Questions
10 Videos
- MAGNETISM AND MATTER BOOK - AAKASH INSTITUTE ENGLISHCHAPTER - MAGNETISM AND MATTER EXERCISE - ASSIGNMENT (SECTION D)
26 Videos
Similar Questions
A wheel of radius R=10cm and moment of inertia I=0.05kgm2 is rotating about a fixed horizontal axis O with angular velocity ω0=10rads−1. A uniform riigid rod of mass m=3kg and length l=50cm is hinged at one end A such that it can rotate at end A in a vertical plane. End B of the rod is tied with a thread as shown in figure such that the rod is horizontal and is just in contact with the surface of rotating wheel. Horizontal distance between axis of rotation O of cylinder and A is equal to a=30cm.
If the wheel stops rotating after one second after the thread has burnt, calculate coefficient of friction ,μ between the rod and the surface of the wheel. (g=10ms−2)

View SolutionA small coin of mass 40 g is placed on the horizontal surface of a rotating disc. The disc starts from rest and is given a constant angular acceleration α=2 rad s−2. The coefficient of static friction between the coin and the disc is μs=3/4 and the coefficient of kinetic friction is μk=0.5. The coin is placed at a distance r=1m from the centre of the disc. The magnitude of the resultant force on the coin exerted by the disc just before it starts slipping on the disc is?
View SolutionA small coin of mass 80g is placed on the horizontal surface of a rotating disc. The disc starts from rest and is given a constant angular acceleration α=2rad/s2. The coefficient of static friction between the coin and the disc is μs=3/4 and cofficient of kinetic friction is μk=0.5. The coin is placed at a distance r=1m from the centre of the disc. The magnitude of the resultant force on the coin exerted by the disc just before it starts slipping on the disc is

View SolutionA small coin of mass 80g is placed on the horizontal surface of a rotating disc. The disc starts from rest and is given a constant angular acceleration α=2rad/s2. The coefficient of static friction between the coin and the disc is μs=3/4 and cofficient of kinetic friction is μk=0.5. The coin is placed at a distance r=1m from the centre of the disc. The magnitude of the resultant force on the coin exerted by the disc just before it starts slipping on the disc is

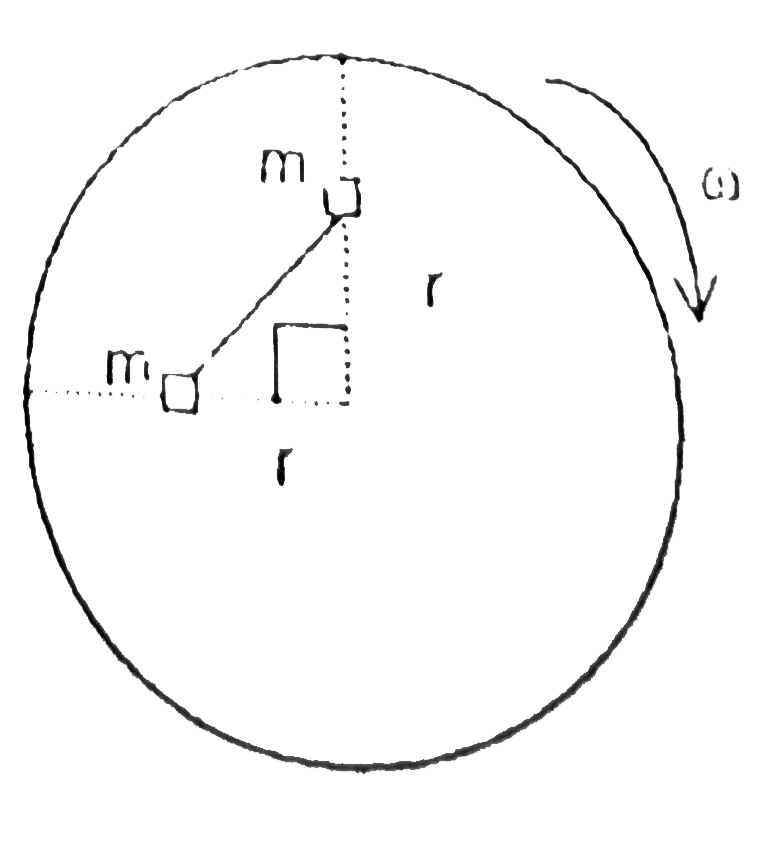
View SolutionTwo particles of mass M=3kg each are kept on a horizontal circular platform on two mutually perpendicular radii at equal distance R=1m from the centre of the table. The particles are connected with a string,which is just taught when the platform is not rotating.Coefficient of friction between the platform and block is μ=0.4.Then the maximum angular speed (ω in radsec) of platform about its centre so that the blocks remain stationary relative to platform is (take g=10.ms2 )
View SolutionTwo particles of mass m each are kept on a horizontal circular platfrom on two mutually perpendicular radii at equal distance r from the center of the table. The particles are connected with a string, which is just taught when the platfrom is not rotating. The coefficient of static friction between the platfrom and block is μ (now if angular speed of platfrom m is slowly increased). Find the maximum angular speed (ω) of platfrom about it center so that the blocks remain stationery relative to platform. (If μ=1√2, r=2.5m and g=10m/s2)
View SolutionA grinding machine whose wheel has a radius of 1π is rotating at 2.5 rev/sec. A tool to be shar-pened is held against the wheel with a force of 40N. If the coefficient of friction between the tool and wheel is 0.2, power required is
View SolutionA boy (30 kg) sitting on his horse whips it. The horse speeds up at an average acceleration of 2.0ms2. A. If the boy does not slide back, what is the force of friction exerted by the horse on the boy? b.If the boy slides back during the acceleration, what can be said about the coefficient of static friction between the horse and the boy. Take g=10ms2
View SolutionA coin is placed at the edge of a horizontal disc rotating about a vertical axis through its axis with a uniform angular speed 2 rad s−1. The radius of the disc is 50 cm. Find the minimum coefficient of friction between disc and coin so that the coin does not slip. (Take g=10m/s2)
View SolutionA block of mass 1kg is placed on the periphery of a rotating rough circular table of radius 50cm as shown in the figure.Angular velocity of the table is 4 rad/s.The minimum value of coefficient of friction between the contact such that there is no relative slipping is (g=10ms2)
_PHY_E05_167_Q01.png)
View Solution
