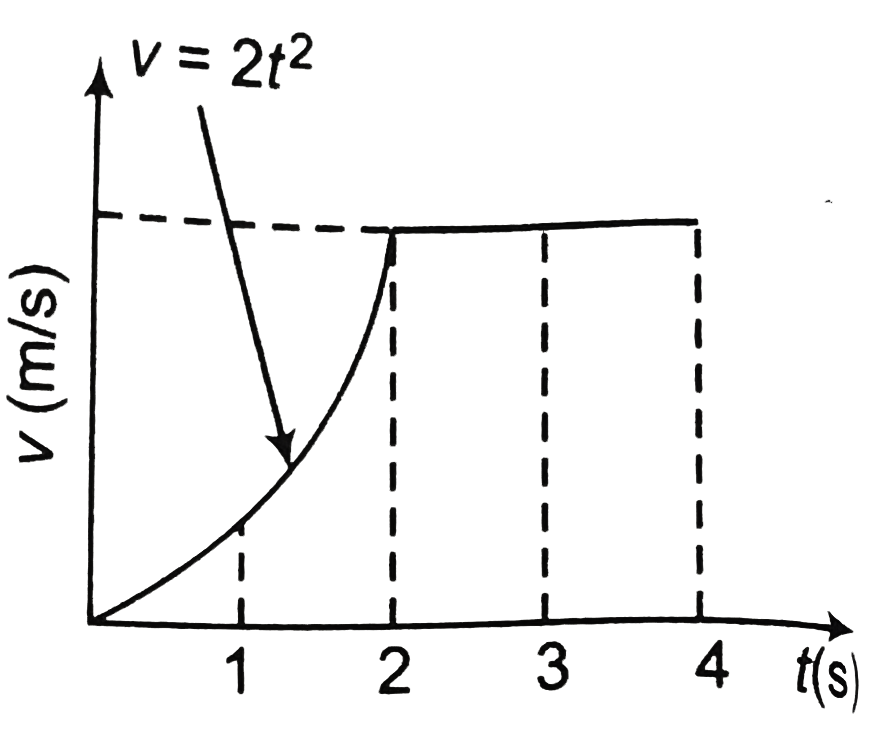
A car begains from rest at time t=0, and then acceleration along a straight track during the interval 0<t≤2s and thereafter with constant velocity as shown in figure in the graph. A coin is initially at rest on the floor of the car. At t=1s, the coin begains to slip and its stops slipping at t=3s . The coefficient of static friction between the floor and the coin is (g=10m/s2)
0.2
0.3
0.4
0.5
The correct Answer is:C
v=2t2
∴a=dvdt=4t At t=1s,
a=4m/s2 …(i)
Limiting value of static friction ,
fL=μSmg
∴ Maximum value of acceleration of coin which can be provided by the friction ,
amax=fLm=μSmg
Equating Eqs. (i) and (ii), we get
4=μS(10)
μS=0.4
Topper's Solved these Questions
- LAWS OF MOTIONBOOK - DC PANDEY ENGLISHCHAPTER - LAWS OF MOTIONEXERCISE - Objective Question
32 Videos
- LAWS OF MOTIONBOOK - DC PANDEY ENGLISHCHAPTER - LAWS OF MOTIONEXERCISE - Comprehension
9 Videos
- LAWS OF MOTIONBOOK - DC PANDEY ENGLISHCHAPTER - LAWS OF MOTIONEXERCISE - Assertion And Reason
28 Videos
- KINEMATICS 1BOOK - DC PANDEY ENGLISHCHAPTER - KINEMATICS 1EXERCISE - INTEGER_TYPE
15 Videos
- LAWS OF THERMODYNAMICSBOOK - DC PANDEY ENGLISHCHAPTER - LAWS OF THERMODYNAMICSEXERCISE - Level 2 Subjective
18 Videos
Similar Questions
A car starts from rest at time t = 0 and it a-t graph is shown in figure. A coin is initially at rest on the floor of the car. At t = 1 s the coin begins to slip and it stops slipping at t = 3 s. The coefficient of static friction between the floor and the coin is (g = 10 m/s2)
_PHY_E05_188_Q02.png)
View SolutionA long plank begins to move at t=0 and accelerates along a straight track wit a speed given by v=2t2 for 0≤t≤2 (where v is in m/s and t is in second). After 2 sec the plane continues to move at the constant speed acquired. A small initially at rest on the plank begins to slip at t=1 sec and stops sliding at t=3 sec. If the coefficient of static friction and kinetic friction between the plank and the block is 0.s and 0.k (where s and k are digits) respectively, find s+k (take g=10m/s2)
View SolutionA car starts from rest and moves with uniform acceleration a on a straight road from time t=0 to t=T. After that, a constant deceleration brings it to rest. In this process the average speed of the car is
View SolutionA car starts from rest and moves with uniform acceleration a on a straight road from time t=0 to t=T. After that, a constant deceleration brings it to rest. In this process the average speed of the car is
View SolutionA car accelerates from rest with 2ms−2 for 2s and then decelerates constantly with 4ms−2 for t0 second to come to rest. The graph for the motion is shown in figure.

a. Find the maximum speed attained by the car.
b. Find the value of t0.
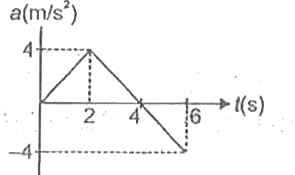
View SolutionFor the acceleration - time (a - t) graph shown in figure, the change in velocity of particle from t = 0 to t = 6 s is
View SolutionThe acceleration (a)-time(t) graph for a particle moving along a straight from rest is shown in figure. Which of the following graph is the best representation of its velocity (v) with time (t) ?
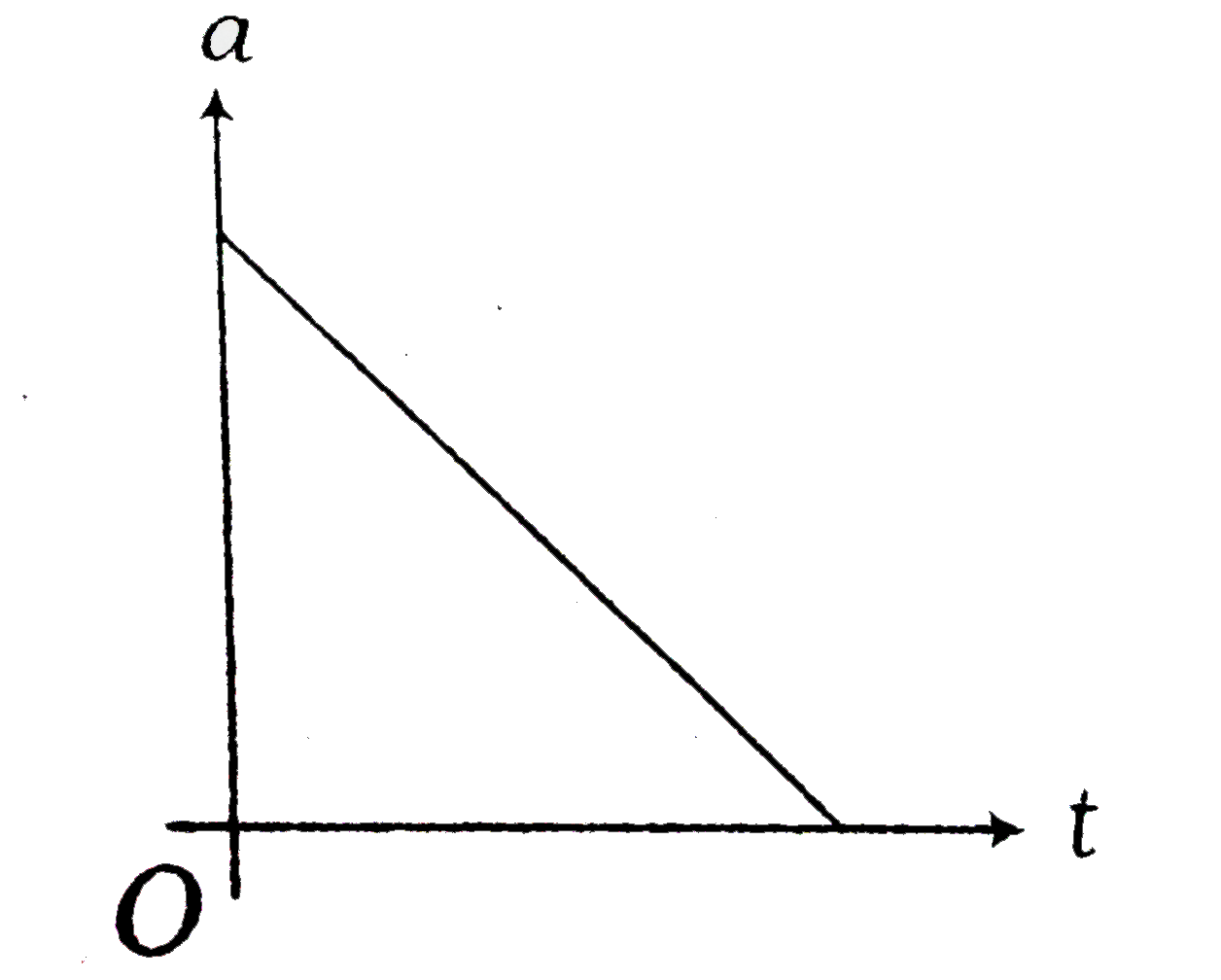
View SolutionA particle, starting from rest, moves in a straight line with constant acceleration a0 for a time interval t0.Then is accelerates at a constant rate 2a0 for time interval 2t0 .The distance travelled by the particle in time 3t0 from the starts is S . Then Sa0t20=
View SolutionInitially car A is 10.5m ahead of car B. Both start moving at time t=0 in the same direction along a straight line. The velocity-time graph of two cars is shown in figure. The time when the car B will catch the car A, will be.

View SolutionIf a=(3t2+2t+1) ms2 is the expression according to which the acceleration of a particle varies. Then-
The expression for instantaneous velocity at any time t will be (if the particle was initially at rest)-
View Solution
