Question

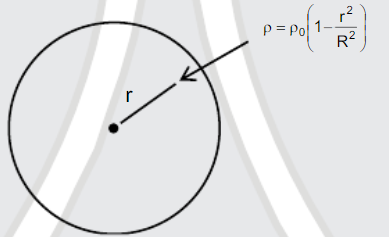
Consider a solid sphere oF radius R and mass density $\rho \left(r\right)={\rho }_0(1-\frac{r^2}{R^2})$ $0<r\le R$. The minimum density oF a liquid in which it will Float is:

Options

A. `(rho_(0))/(3)`
B. `(2rho_(0))/(5)`
C. `(2rho_(0))/(3)`
D. `(rho_(0))/(5)`

Answer

2

Explanation

To solve the problem, we need to find the minimum density of a liquid in which a solid sphere with a given density profile will float. The density of the sphere is given by:

$$\rho \left(r\right)={\rho }_0(1-\frac{r^2}{R^2})\text{for}0<r\le R$$

Step 1: Calculate the Mass of the Sphere

To find the mass of the sphere, we need to integrate the density over the volume of the sphere. The volume element in spherical coordinates is given by \(dV = 4\pi r^2 dr\). Thus, the mass \(M\) of the sphere can be calculated as follows:

\( M = \int_0^R \rho(r) \, dV = \int_0^R \rho(r) \, 4\pi r^2 \, dr \)

Substituting the expression for \(\rho(r)\):

\( M = \int_0^R \rho_0 \left(1 - \frac{r^2}{R^2}\right) 4\pi r^2 \, dr \)

Step 2: Simplify the Integral

We can simplify the integral:

\( M = 4\pi \rho_0 \int_0^R \left(r^2 - \frac{r^4}{R^2}\right) dr \)

This can be split into two separate integrals:

\( M = 4\pi \rho_0 \left( \int_0^R r^2 \, dr - \frac{1}{R^2} \int_0^R r^4 \, dr \right) \)

Step 3: Evaluate the Integrals

Now we evaluate the integrals:

1. \(\int_0^R r^2 \, dr = \frac{R^3}{3}\)
2. \(\int_0^R r^4 \, dr = \frac{R^5}{5}\)

Substituting these results back into the equation for \(M\):

\( M = 4\pi \rho_0 \left( \frac{R^3}{3} - \frac{1}{R^2} \cdot \frac{R^5}{5} \right) \)

Step 4: Simplify the Expression for Mass

Now, we can simplify the expression for mass \(M\):

\( M = 4\pi \rho_0 \left( \frac{R^3}{3} - \frac{R^3}{5} \right) \)

Finding a common denominator (15):

\( M = 4\pi \rho_0 \left( \frac{5R^3}{15} - \frac{3R^3}{15} \right) = 4\pi \rho_0 \left( \frac{2R^3}{15} \right) \)

Thus, the mass of the sphere is:

\( M = \frac{8\pi \rho_0 R^3}{15} \)

Step 5: Calculate the Volume of the Sphere

The volume \(V\) of the sphere is given by:

\( V = \frac{4}{3} \pi R^3 \)

Step 6: Apply Archimedes' Principle

For the sphere to float, the buoyant force must equal the weight of the sphere. The buoyant force \(F_b\) is given by:

\( F_b = \rho_l g V \)

where \(\rho_l\) is the density of the liquid and \(g\) is the acceleration due to gravity. The weight of the sphere \(W\) is given by:

\( W = Mg = \frac{8\pi \rho_0 R^3}{15} g \)

Setting the buoyant force equal to the weight:

\( \rho_l g \cdot \frac{4}{3} \pi R^3 = \frac{8\pi \rho_0 R^3}{15} g \)

Step 7: Solve for the Density of the Liquid

Canceling \(g\) and \(\pi R^3\) from both sides:

\( \rho_l \cdot \frac{4}{3} = \frac{8 \rho_0}{15} \)

Now, solving for \(\rho_l\):

\( \rho_l = \frac{8 \rho_0}{15} \cdot \frac{3}{4} = \frac{2 \rho_0}{5} \)

Final Answer

Thus, the minimum density of the liquid in which the sphere will float is:

\( \boxed{\frac{2\rho_0}{5}} \)