A capacitance of is required in an electrical circuit across a potential difference of A large number of capacitors are available which can withstand a potential difference of not more than .
The minimum number of capacitors required to achieve this is
The correct Answer is:B
To solve the problem, we need to determine the minimum number of capacitors required to achieve a capacitance of 2 μF across a potential difference of 1 kV, using 1 μF capacitors that can withstand a maximum potential difference of 300 V.
1. Determine the number of capacitors in series:
Each capacitor can withstand a maximum voltage of 300 V. To achieve a total voltage of 1 kV (1000 V), we need to find how many capacitors are required in series.
Number of capacitors in series (n)=1000 V300 V=103≈3.33
Since we cannot have a fraction of a capacitor, we round up to the nearest whole number:
n=4
2. Calculate the equivalent capacitance of capacitors in series:
The formula for the equivalent capacitance Cs of capacitors in series is given by:
1Cs=1C1+1C2+…+1Cn
For n capacitors of capacitance C=1μF:
1Cs=nC=41μF⟹Cs=1μF4=0.25μF
3. Determine the number of rows of capacitors in parallel:
Now, we need to achieve a total capacitance of 2 μF. If we have m rows of Cs=0.25μF in parallel, the total capacitance Ctotal is given by:
Ctotal=m⋅Cs=m⋅0.25μF
Setting this equal to the required capacitance:
m⋅0.25μF=2μF⟹m=2μF0.25μF=8
4. Calculate the total number of capacitors:
The total number of capacitors used is the product of the number of capacitors in series and the number of rows:
Total capacitors=n⋅m=4⋅8=32
Final Answer:
The minimum number of capacitors required is 32.
Each capacitor can withstand a maximum voltage of 300 V. To achieve a total voltage of 1 kV (1000 V), we need to find how many capacitors are required in series.
Number of capacitors in series (n)=1000 V300 V=103≈3.33
Since we cannot have a fraction of a capacitor, we round up to the nearest whole number:
n=4
The formula for the equivalent capacitance Cs of capacitors in series is given by:
1Cs=1C1+1C2+…+1Cn
For n capacitors of capacitance C=1μF:
1Cs=nC=41μF⟹Cs=1μF4=0.25μF
Now, we need to achieve a total capacitance of 2 μF. If we have m rows of Cs=0.25μF in parallel, the total capacitance Ctotal is given by:
Ctotal=m⋅Cs=m⋅0.25μF
Setting this equal to the required capacitance:
m⋅0.25μF=2μF⟹m=2μF0.25μF=8
The total number of capacitors used is the product of the number of capacitors in series and the number of rows:
Total capacitors=n⋅m=4⋅8=32
The minimum number of capacitors required is 32.
Topper's Solved these Questions
Similar Questions
An electrical technician requires a capacitance of 2μF in a circuit across a potential difference of 1 kV. A large number of 1μF capacitors are available to him each of which can withstand a potential difference of not more than 400 V. Suggest a possible arrangement that requires the minimum number of capacitors.
View SolutionIn the arrangement shown, a potential difference is applied between points A and B. No capacitor can withstand a potential difference of more than 100 V
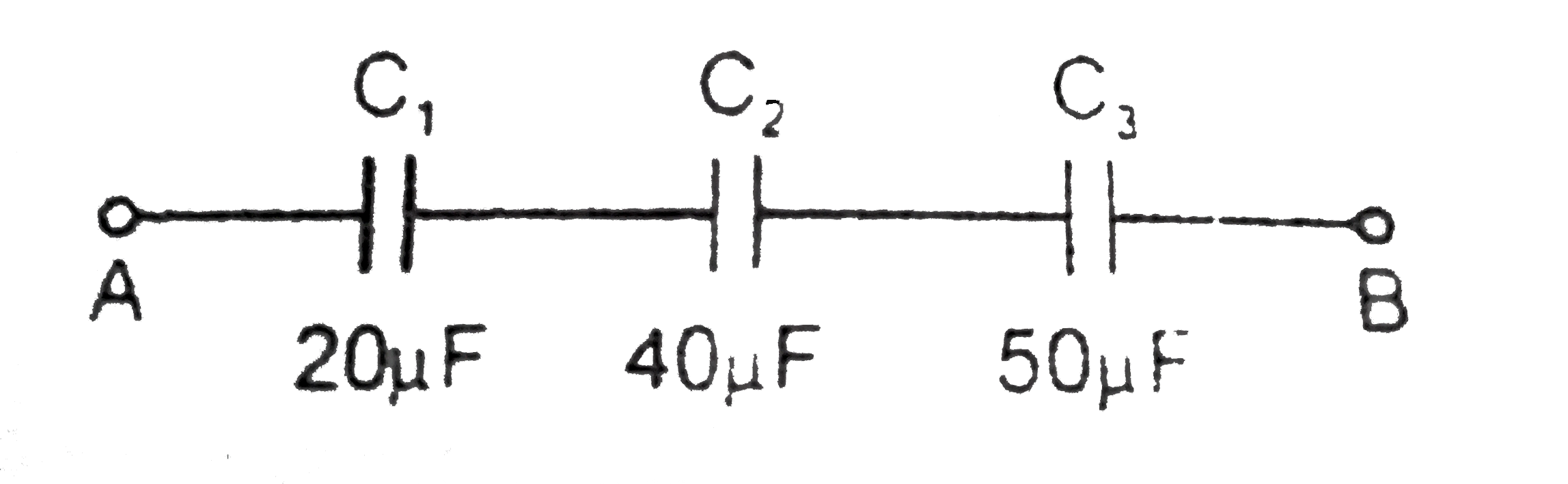
View SolutionWhile working on a physics project at school physics, lab, you require a 4 μF capacitor in a circuit across a potential difference of 1 k V. Unfortunately, 4 μF capacitors are out or stock in your lab but 2 μF capacitors which can withstand a potential difference of 400 V are available in plenty . if you decide to use the 2 μF capacitors in place of 4μ F capacitor minimum number of capacitors required are
View Solutiongiven that potential differene across 1μF capacitor is 10V. Then,
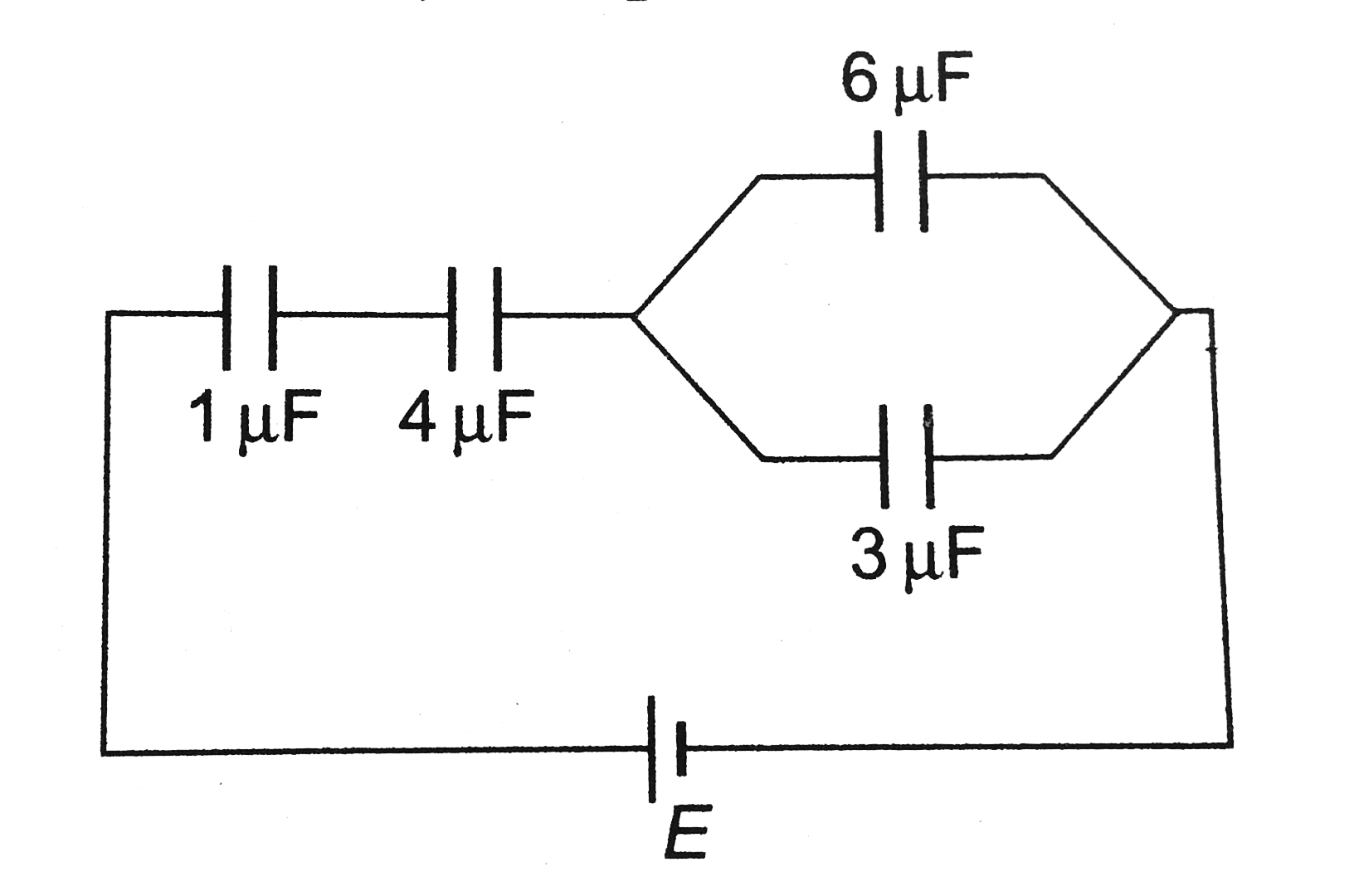
View SolutionThe energy stored in a capacitor of capacitance 100μF is 50 J. Its potential difference is
View SolutionIn the circuit shown in the figure, the potential difference across the 4.5μF capacitor is
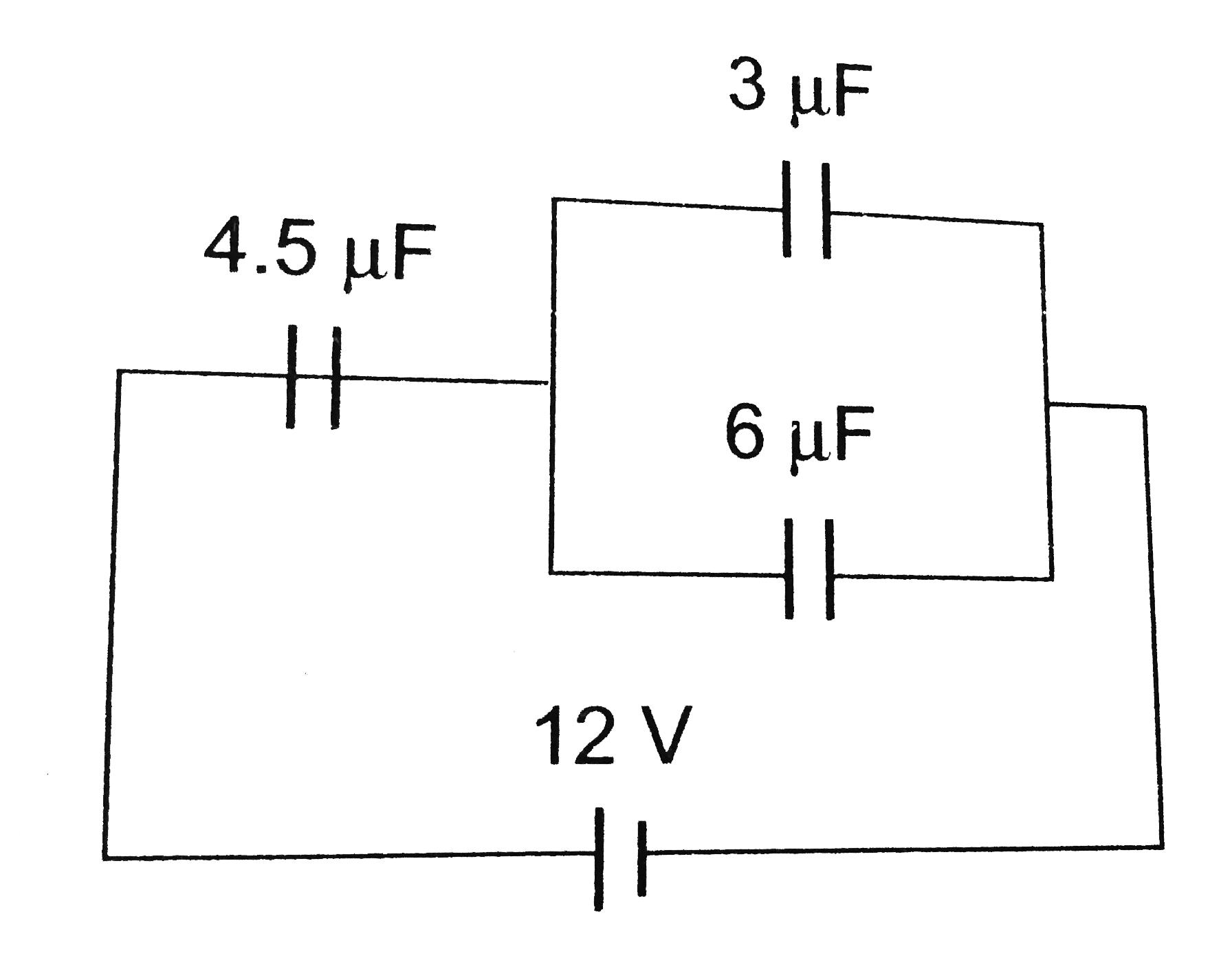
View SolutionA 10μF capacitor is charged to a potential difference of 50V and is connected to another uncharged capacitor in parallel. Now the common potential difference becomes 20 volt. The capacitance of second capacitor is
View SolutionA 10μF capacitor is charged to a potential difference of 50V and is connected to another uncharged capacitor in parallel. Now the common potential difference becomes 20 volt. The capacitance of second capacitor is
View SolutionFind the energy stored in a capacitor of capacitance 100μF when it is charged to a potential difference of 20 V.
View SolutionA 100μF capacitor is charged to a potential difference of 24V. It is connected to an uncharged capacitor of capacitance 20μF What will be the new potential difference across the 100μF capacitor?
View Solution
