Question

Number of the $\alpha$- particle deflected in Rutherford's $\alpha$ -scattering experiment varies with the angle of deflection. Then the graph between the two is best represented by.

Options

A.
B.
C.
D.

Explanation

To solve the problem regarding the relationship between the number of alpha particles deflected in Rutherford's alpha-scattering experiment and the angle of deflection, we can follow these steps:

1. Understanding Alpha Scattering:
- In Rutherford's experiment, alpha particles are directed towards a thin gold foil. Most of the alpha particles pass through the foil without any deflection, while a small fraction are deflected at various angles.

2. Deflection Angles:
- The deflection angle (θ) can range from 0° (no deflection) to 180° (backscattering). At 0°, the number of alpha particles is at its maximum, while at 180°, the number is significantly lower.

3. Relationship Between Deflection and Number of Particles:
- The number of alpha particles deflected at a certain angle θ is inversely related to the sine of that angle raised to a power. Specifically, it can be expressed as:
\( N(\theta) \propto \frac{1}{\sin^4(\theta)} \)
- This means that as the angle θ increases, the number of deflected alpha particles decreases rapidly.

4. Graphical Representation:
- If we plot the number of deflected alpha particles (N) against the angle of deflection (θ), we will observe that:
- At θ = 0°, N is maximum (theoretically infinite).
- As θ approaches 180°, N approaches zero.
- The graph will show a steep decline as θ increases, demonstrating the inverse relationship.

5. Conclusion:
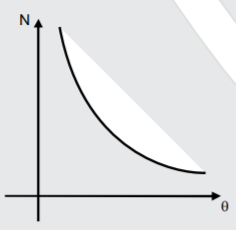
- Therefore, the graph between the number of deflected alpha particles and the angle of deflection is best represented by a curve that decreases sharply as θ increases, confirming the relationship \( N(\theta) \propto \frac{1}{\sin^4(\theta)} \).

Final Answer:
The graph between the number of alpha particles deflected and the angle of deflection is best represented by the relation \( N(\theta) \propto \frac{1}{\sin^4(\theta)} \).