A rod length L has non-uniform linear mass density given by ρ(x)=a+b(XL)2 where a and b are constant and 0≤x≤L. The value of x for the centre of mass of the rod is at :
3l4(3a+b2a+b)
3l4(2a+b3a+b)
l4(2a+b3a+b)
l(2a+b3a+b)
The correct Answer is:B
Step by step video & image solution for A rod length L has non-uniform linear mass density given by rho(x)=a+b((X)/(L))^(2) where a and b are constant and 0lexleL. The value of x for the centre of mass of the rod is at : by Physics experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Topper's Solved these Questions
Similar Questions
The density of a non-uniform rod of length 1m is given by ρ(x)=a(1+bx2)
where a and b are constants and 0≤x≤1.
The centre of mass of the rod will be at
View SolutionThe linear density of a non−uniform rod of length 2m is given by λ(x)=a(1+bx2) where a and b are constants and 0≤x≤2. The centre of mass of the rod will be at. X=
View Solution
Knowledge Check
The density of a non-uniform rod of length 1m is given by ρ(x)=a(1+bx2)
where a and b are constants and 0≤x≤1.
The centre of mass of the rod will be atA3(2+b)4(3+b)B4(2+b)3(3+b)C3(3+b)4(2+b)D4(3+b)3(2+b)
You are given a rod of length L. The linear mass density is λ such that λ=a+bx. Here a and b are constants and the mass of the rod increases as x decreases. Find the mass of the rod

View SolutionThe centre of mass of a non uniform rod of length L, whose mass per unit length varies as ρ=k.x2L where k is a constant and x is the distance of any point from one end is (from the same end)
View SolutionA thin rod of length L is lying along the x-axis with its ends at x=0 and x=L its linear (mass/length) varies with x as k(xL)n, where n can be zero of any positive number. If to position xCM of the centre of mass of the rod is plotted against 'n', which of the following graphs best apporximates the dependence of xCM on n?
View SolutionA rod hanging from ceiling has linear density given as λ=m0(1+x) kg/m, where m0 is constant and x is distance of a point from free end . if the length of the rod is 4m then velocity of wave at x=1m is
View SolutionA uniform thin rod AB of length L has linear mass density μ(x)=a+bxL, where x is measured from A. If the CM of the rod lies at a distance of (712L) from A, then a and b are related as :_
View SolutionA rod of length L is placed along the x-axis between x=0 and x=L. The linear mass density (mass/length) ρ of the rod varies with the distance x from the origin as ρ=a+bx. Here, a and b are constants. Find the position of centre of mass of this rod.
View SolutionThe adjacent figure shows a non-uniform metre stick AB having the linear mass density variation λ=λ0x , where λ0 is a constant and x is the distance from end A, placed on a smooth horizontal surface. In the first experiment, the rod is pivoted at A and force F is applied perpendicular to the rod at the other end B and in the second experiment, the rod is pivoted at B and the force is applied perpendicular to the rod at the end A. If in the first case angular acceleration is αA and in the second case it is αB then
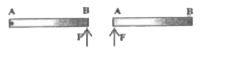
View Solution
