Consider two charged metallic spheres , and , of radii , and respectively. The electric fields , (on ,) and , (on ) their surfaces are such that . Then the ratio (on )/ (on ) of the electrostatic potential on each sphere is
The correct Answer is:1
To solve the problem, we need to find the ratio of the electrostatic potentials V1 and V2 on the surfaces of the two charged metallic spheres S1 and S2 respectively. Given that the electric fields E1 and E2 on the surfaces of the spheres satisfy the condition E1E2=R1R2, we can proceed with the following steps:
1. Understanding Electric Field and Potential:
The electric field E at the surface of a charged metallic sphere is given by:
E=kQR2
where k is Coulomb's constant, Q is the charge on the sphere, and R is the radius of the sphere.
2. Relating Electric Field to Potential:
The electrostatic potential V at the surface of a charged sphere is given by:
V=kQR
3. Expressing Electric Field in Terms of Potential:
We can express the electric field E in terms of the potential V:
E=VR
Therefore, for sphere S1:
E1=V1R1
and for sphere S2:
E2=V2R2
4. Finding the Ratio of Potentials:
From the expressions for electric fields, we can write:
V1=E1R1
V2=E2R2
Thus, the ratio of potentials becomes:
V1V2=E1R1E2R2
5. Substituting the Given Condition:
We know from the problem statement that:
E1E2=R1R2
Substituting this into our equation for the ratio of potentials gives:
V1V2=R1R2⋅R1R2=(R1R2)2
6. Final Result:
Therefore, the ratio of the electrostatic potentials on the surfaces of the two spheres is:
V1V2=(R1R2)2
Conclusion:
The final answer is:
V1V2=(R1R2)2
The electric field E at the surface of a charged metallic sphere is given by:
E=kQR2
where k is Coulomb's constant, Q is the charge on the sphere, and R is the radius of the sphere.
The electrostatic potential V at the surface of a charged sphere is given by:
V=kQR
We can express the electric field E in terms of the potential V:
E=VR
Therefore, for sphere S1:
E1=V1R1
and for sphere S2:
E2=V2R2
From the expressions for electric fields, we can write:
V1=E1R1
V2=E2R2
Thus, the ratio of potentials becomes:
V1V2=E1R1E2R2
We know from the problem statement that:
E1E2=R1R2
Substituting this into our equation for the ratio of potentials gives:
V1V2=R1R2⋅R1R2=(R1R2)2
Therefore, the ratio of the electrostatic potentials on the surfaces of the two spheres is:
V1V2=(R1R2)2
The final answer is:
V1V2=(R1R2)2
Topper's Solved these Questions
Similar Questions
Consider two charged metallic spheres S1andS2 of radii 3R and R, respectively. The electric potential V1(onS1)and(onS2) on their surfaces are such that V1V2=41. Then the ratio E1onS1E2(onS2) of the electric fields on their surfaces is:
View SolutionConsider two charged metallic spheres S1andS2 of radii 3R and R, respectively. The electric potential V1(onS1)and(onS2) on their surfaces are such that V1V2=41. Then the ratio E1onS1E2(onS2) of the electric fields on their surfaces is:
View SolutionConsider two charged metallic spheres S1 and S2 of radii R and 4R, respectively. The electric fields E1 (on S1 ) and E2 (on S2) on their surfaces are such that E1E2=51 . Then the ratio V1 (on S1 ) / V1 (on S2 ) of the electrostatic potentials on each sphere is :
View SolutionTwo charged spheres of radii R1andR2 having equal surface charge density. The ratio of their potential is
View SolutionTwo spheres of radii R1 and R1 respectively are charged and joined by wire. The ratio of electric field of spheres is
View SolutionConsider two solid sphere of radii R1=1m,R2=2m and masses M1andM2, respectively. The gravitational field due to sphere 1 and 2 are shown. The value of M1M2) is:
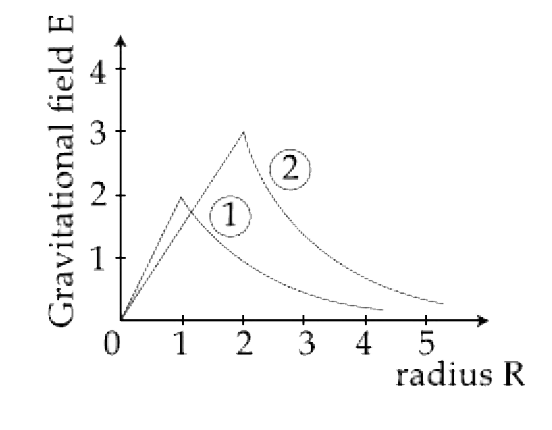
View SolutionThree plates A, B and C are placed close to each other with +Q charge given to the middle plate. The inner surfaces to A and C can be connected to earth through plate D and keys K1 and K2 . The plates D is a dielectric slab with dielectric constant K1 then the charge that will flow through plate D and keys K1 and K2 . The plate D is a dielectric slab with dielectric constant K, then the charge that will flow though plate D when K2 is closed and K2 is open is

View SolutionTwo concentric, thin metallic spheres of radii R1andR2(R1>R2) charges Q1andQ2 respectively Then the potential at radius r between R1andR2 will be (k=1/4π∈)
View SolutionThe insulated spheres of radii R1 and R2 having charges Q1 and Q2 respectively are connected to each other. There is
View SolutionThe insulated spheres of radii R1 and R2 having charges Q1 and Q2 respectively are connected to each other. There is
View Solution
