An object is moving away from concave mirror of focal length f starting from focus. The distance of an object from pole of mirror is x. The correct graph of magnitude of magnification(m) verses distance x is:
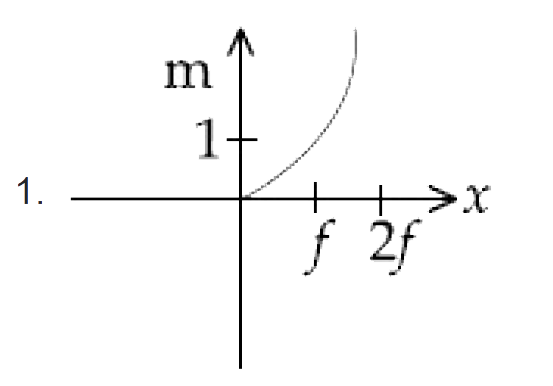
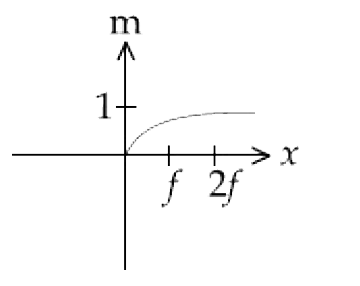
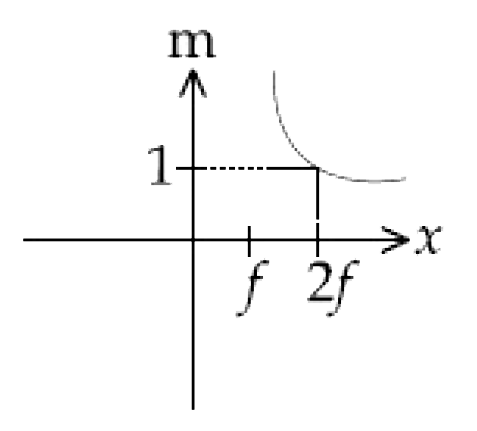
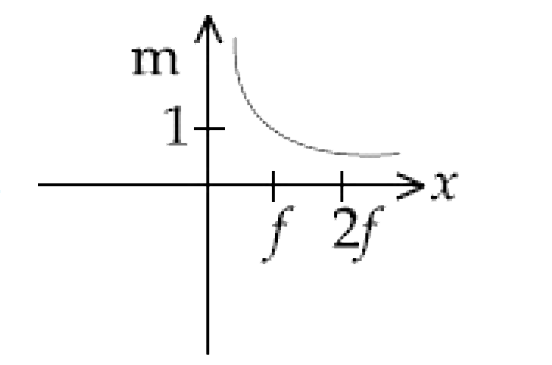
The correct Answer is:3
To solve the problem of finding the correct graph of the magnitude of magnification (m) versus the distance (x) for an object moving away from a concave mirror, we can follow these steps:
Step 1: Understand the Mirror Formula
The mirror formula for a concave mirror is given by:
1v+1u=1f
where:
- v = image distance
- u = object distance (negative for concave mirrors)
- f = focal length (negative for concave mirrors)
Step 2: Set the Initial Conditions
The object starts at the focus of the mirror, so:
- At the focus, u=−f (since object distances are taken as negative in mirror convention).
- Therefore, at this point, we can calculate the image distance v.
Step 3: Calculate Magnification at the Focus
The magnification m is defined as:
m=−vu
At u=−f:
- From the mirror formula, substituting u=−f:
1v+1−f=1f
This simplifies to:
1v=2f⟹v=f2
Now substituting v into the magnification formula:
m=−f2−f=12
However, as the object is at the focus, the image distance approaches infinity, leading to infinite magnification.
Step 4: Calculate Magnification at x=2f
Now, let’s consider when x=2f:
- Here, u=−2f.
- Using the mirror formula:
1v+1−2f=1f
This simplifies to:
1v=1f+12f=32f⟹v=2f3
Now substituting v into the magnification formula:
m=−2f3−2f=13
Step 5: Analyze the Behavior of Magnification as x Increases
As the object moves further away from the mirror (increasing x):
- The image distance v will decrease in magnitude.
- Consequently, the magnification m will approach zero but remain negative, indicating that the image is inverted and diminishing in size.
Step 6: Determine the Graph Characteristics
- At x=f, m is infinite.
- At x=2f, m=−1.
- As x increases beyond 2f, m approaches zero.
Conclusion
The correct graph of the magnitude of magnification |m| versus distance x will show:
- A vertical asymptote at x=f (where m is infinite).
- A value of |m|=1 at x=2f.
- A decreasing curve approaching zero as x increases.
The mirror formula for a concave mirror is given by:
1v+1u=1f
where:
- v = image distance
- u = object distance (negative for concave mirrors)
- f = focal length (negative for concave mirrors)
The object starts at the focus of the mirror, so:
- At the focus, u=−f (since object distances are taken as negative in mirror convention).
- Therefore, at this point, we can calculate the image distance v.
The magnification m is defined as:
m=−vu
At u=−f:
- From the mirror formula, substituting u=−f:
1v+1−f=1f
This simplifies to:
1v=2f⟹v=f2
Now substituting v into the magnification formula:
m=−f2−f=12
However, as the object is at the focus, the image distance approaches infinity, leading to infinite magnification.
Now, let’s consider when x=2f:
- Here, u=−2f.
- Using the mirror formula:
1v+1−2f=1f
This simplifies to:
1v=1f+12f=32f⟹v=2f3
Now substituting v into the magnification formula:
m=−2f3−2f=13
As the object moves further away from the mirror (increasing x):
- The image distance v will decrease in magnitude.
- Consequently, the magnification m will approach zero but remain negative, indicating that the image is inverted and diminishing in size.
- At x=f, m is infinite.
- At x=2f, m=−1.
- As x increases beyond 2f, m approaches zero.
The correct graph of the magnitude of magnification |m| versus distance x will show:
- A vertical asymptote at x=f (where m is infinite).
- A value of |m|=1 at x=2f.
- A decreasing curve approaching zero as x increases.
Topper's Solved these Questions
Similar Questions
Knowledge Check
An object is kept on the principal axis of a concave mirror of focal length 10cm, at a distance of 15 cm from its pole. The image formed by the mirror is:
AVirtual and magnifiedBVirtual and diminishedCReal and magnifiedDReal and diminished
An object is placed at a distance f in the front of a convex mirror. If focal length of the mirror is f, then distance of image from pole of the mirror is
View SolutionFor a concave mirror of focal length f, image is 2 times larger. Then the object distance from the mirror can be
View SolutionThe image formed by a convex mirror of focal length 30cm. is a quarter of the object. What is the distance of the object from the mirror ?
View SolutionAn object is moving towards a concave mirror of focal length 24 cm. When it is at a distance of 60 cm from the mirror, its speed is 9cm/s. The speed of its image at that instant , is
View SolutionA convex mirror of focal length f produced an image (1/n)th of the size of the object. The distance of the object from the mirror is
View SolutionAn object is gradually moving away from the focal point of a converging lens along the axis of the lens. The graphical representation of the magnitude of linear magnification (m) versus distance of the object from the lens (x) is correctly given by : (Graphs are drawn schematically and are not to scale)
View SolutionA concave mirror of focal length f produces a real image n times the size of the object. What is the distance of the object from the mirror?
View Solution