An object is gradually moving away from the focal point of a converging lens along the axis of the lens. The graphical representation of the magnitude of linear magnification (m) versus distance of the object from the lens (x) is correctly given by : (Graphs are drawn schematically and are not to scale)

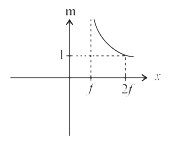
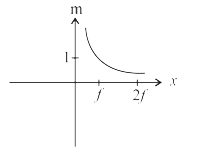
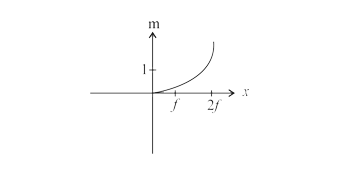
The correct Answer is:B
To solve the problem of determining the correct graphical representation of the magnitude of linear magnification (m) versus the distance of the object from the lens (x) for a converging lens, we can follow these steps:
Step 1: Understand the Lens Formula
The lens formula is given by:
1v−1u=1f
Where:
- v is the image distance,
- u is the object distance (negative for real objects),
- f is the focal length (positive for converging lenses).
Step 2: Express Image Distance in Terms of Object Distance
From the lens formula, we can rearrange it to find the image distance v:
v=ufu+f
Step 3: Determine the Magnification
The magnification m is defined as:
m=vu
Substituting the expression for v:
m=ufu+f⋅1u=fu+f
Step 4: Analyze the Behavior of Magnification
As the object distance u increases (the object moves away from the lens):
- When u approaches infinity, m approaches 0.
- When u is equal to f (the focal length), m is 1.
- As u decreases towards f, the magnification increases.
Step 5: Graphical Representation
The relationship between the magnitude of magnification |m| and the object distance |u| can be summarized:
- At u=f, |m|=1.
- As u increases beyond f, |m| decreases towards 0.
- The graph will show a decreasing curve starting from |m|=1 and approaching |m|=0 as u increases.
Conclusion
The correct graphical representation of the magnitude of linear magnification versus the distance of the object from the lens is a curve that starts at |m|=1 when u=f and decreases towards 0 as u approaches infinity. Therefore, the correct option is represented by curve B.
---
The lens formula is given by:
1v−1u=1f
Where:
- v is the image distance,
- u is the object distance (negative for real objects),
- f is the focal length (positive for converging lenses).
From the lens formula, we can rearrange it to find the image distance v:
v=ufu+f
The magnification m is defined as:
m=vu
Substituting the expression for v:
m=ufu+f⋅1u=fu+f
As the object distance u increases (the object moves away from the lens):
- When u approaches infinity, m approaches 0.
- When u is equal to f (the focal length), m is 1.
- As u decreases towards f, the magnification increases.
The relationship between the magnitude of magnification |m| and the object distance |u| can be summarized:
- At u=f, |m|=1.
- As u increases beyond f, |m| decreases towards 0.
- The graph will show a decreasing curve starting from |m|=1 and approaching |m|=0 as u increases.
The correct graphical representation of the magnitude of linear magnification versus the distance of the object from the lens is a curve that starts at |m|=1 when u=f and decreases towards 0 as u approaches infinity. Therefore, the correct option is represented by curve B.
Topper's Solved these Questions
- JEE MAIN REVISION TEST - 27 - JEE -2020BOOK - VMC MODULES ENGLISHCHAPTER - JEE MAIN REVISION TEST - 27 - JEE -2020EXERCISE - PHYSICS (SECTION 2)
5 Videos
- JEE MAIN REVISION TEST - 26 (2020)BOOK - VMC MODULES ENGLISHCHAPTER - JEE MAIN REVISION TEST - 26 (2020)EXERCISE - PHYSICS (SECTION 2)
5 Videos
- JEE MAIN REVISION TEST - 28BOOK - VMC MODULES ENGLISHCHAPTER - JEE MAIN REVISION TEST - 28EXERCISE - PHYSICS (SECTION-2)
5 Videos
Similar Questions
An object is moving away from concave mirror of focal length f starting from focus. The distance of an object from pole of mirror is x. The correct graph of magnitude of magnification(m) verses distance x is:
View SolutionA convex lens of focal length f produces an image 1n times than that of the size of the object. The distance of the object from the lens is:
View SolutionA convex lens produces a real image m times the size of the object. What will be the distance of the object from the lens ?
View SolutionAs an object is moved from the surface of a thin converging lens to a focal point, over what range does the image distance very?
View SolutionA point object O moves from the principal axis of a converging lens in a direction OP. I is the image of O, will move initially in the direction
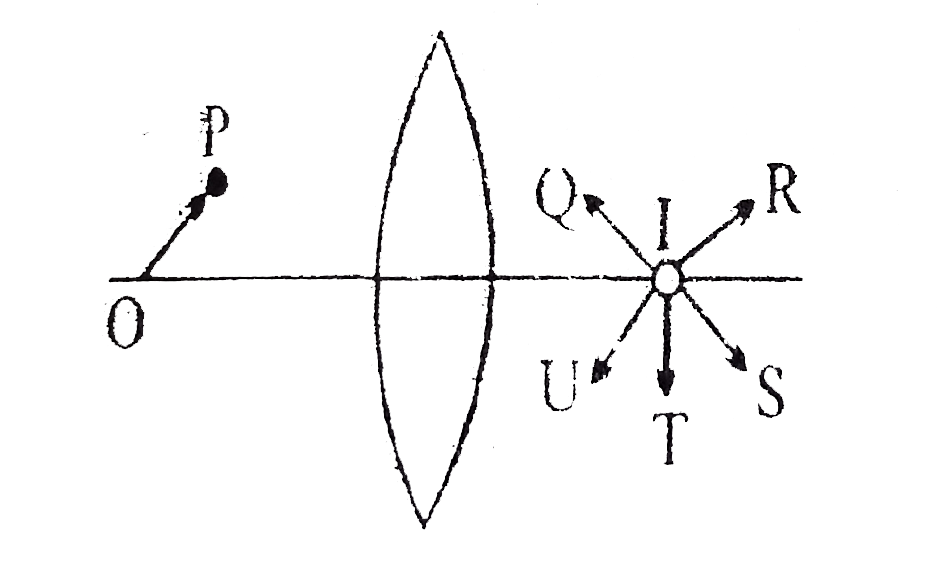
View SolutionA converging lens has a focal length of 0.12 m. To get an image of unit magnification the object should be placed at what distance from the converging lens ?
View SolutionDistance of an object from a concave lens of focal length 20 cm is 40 cm. Then linear magnification of the image
View SolutionAn object is moving towards a converging lens on its axis. The image is also found to be moving towards the lens. Then, the object distance u must satisfy
View SolutionA convex lens of focal length f forms an image which is 1/3 times the size of the object. Then, the distance of object from the lens is
View SolutionA convex lens is used to throw on a screen 10m from the lens, a magnified image of an object. If the magnification is to be 19, find the focal length of the lens.
View Solution
