A positive point charge (q) is projected along (+x) axis with some velocity from origin, electric field is directed along (y) axis Find trajectory of charge in form of x.
Option1
Option2
Option3
Option4
The correct Answer is:A
To solve the problem of finding the trajectory of a positive point charge projected along the x-axis in an electric field directed along the y-axis, we can follow these steps:
Step 1: Understand the motion in the x-direction
Since the charge is projected along the positive x-axis with an initial velocity v0 and there is no electric field acting in the x-direction, the motion in the x-direction is uniform. Therefore, the position of the charge in the x-direction can be expressed as:
x(t)=v0t
Step 2: Analyze the motion in the y-direction
The electric field E is directed along the y-axis, given as E=E0^j. The force F acting on the charge q due to this electric field can be calculated using:
F=qE=qE0
This force will cause an acceleration ay in the y-direction, which can be calculated using Newton's second law:
ay=Fm=qE0m
Step 3: Write the equation of motion in the y-direction
Since the initial velocity in the y-direction is zero (the charge is only projected in the x-direction), we can use the kinematic equation for displacement in the y-direction:
y(t)=uyt+12ayt2
Substituting uy=0 and ay=qE0m, we get:
y(t)=0+12(qE0m)t2=qE02mt2
Step 4: Substitute for time t
From the equation for x(t), we can express time t in terms of x:
t=xv0
Now, substitute this expression for t into the equation for y(t):
y=qE02m(xv0)2
This simplifies to:
y=qE02mv20x2
Step 5: Final trajectory equation
Thus, the trajectory of the charge in the form of y as a function of x is:
y=kx2
where k=qE02mv20.
Summary
The trajectory of the charge projected along the x-axis in the presence of an electric field directed along the y-axis is a parabolic path described by the equation:
y=qE02mv20x2
Since the charge is projected along the positive x-axis with an initial velocity v0 and there is no electric field acting in the x-direction, the motion in the x-direction is uniform. Therefore, the position of the charge in the x-direction can be expressed as:
x(t)=v0t
The electric field E is directed along the y-axis, given as E=E0^j. The force F acting on the charge q due to this electric field can be calculated using:
F=qE=qE0
This force will cause an acceleration ay in the y-direction, which can be calculated using Newton's second law:
ay=Fm=qE0m
Since the initial velocity in the y-direction is zero (the charge is only projected in the x-direction), we can use the kinematic equation for displacement in the y-direction:
y(t)=uyt+12ayt2
Substituting uy=0 and ay=qE0m, we get:
y(t)=0+12(qE0m)t2=qE02mt2
From the equation for x(t), we can express time t in terms of x:
t=xv0
Now, substitute this expression for t into the equation for y(t):
y=qE02m(xv0)2
This simplifies to:
y=qE02mv20x2
Thus, the trajectory of the charge in the form of y as a function of x is:
y=kx2
where k=qE02mv20.
The trajectory of the charge projected along the x-axis in the presence of an electric field directed along the y-axis is a parabolic path described by the equation:
y=qE02mv20x2
Topper's Solved these Questions
Similar Questions
A positively charged particle moving along x-axis with a certain velocity enters a uniform electric field directed along positive y-axis. Its
View SolutionA particle of mass m carrying a positive charge q moves simple harmonically along the x-axis under the action of a varying electric field E directed along the x-axis. The motion of the particle is confined between x=0 and x=2l. The angular frequency of the motion is ω. Then which of the following is correct ?
View SolutionA particle of charge q0 and of mass m0 is projected along the y-axis at t=0 from origin with a velocity V0. If a uniform electric field E0 also exist along the x-axis, then the time at which debroglie wavelength of the particle becomes half of the initial value is:
View SolutionOne long conductor carries current I along y-axis with charge density λ. An electric field exists along z-axis. In what direction, a charged particle at point P, distance x apart from the wire (along x-axis), be projected with velocity v so that it moves undeflected?

View SolutionAn electron beam projected along + X-axis, experience a force due to a magnetic field along the + Y-axis. What is the direction of the magnetic field?
View SolutionA beam of α particles projected along + x-axis, experiences a force due to a magnetic field along the +y-axis figure. What is the direction of magnetic field.
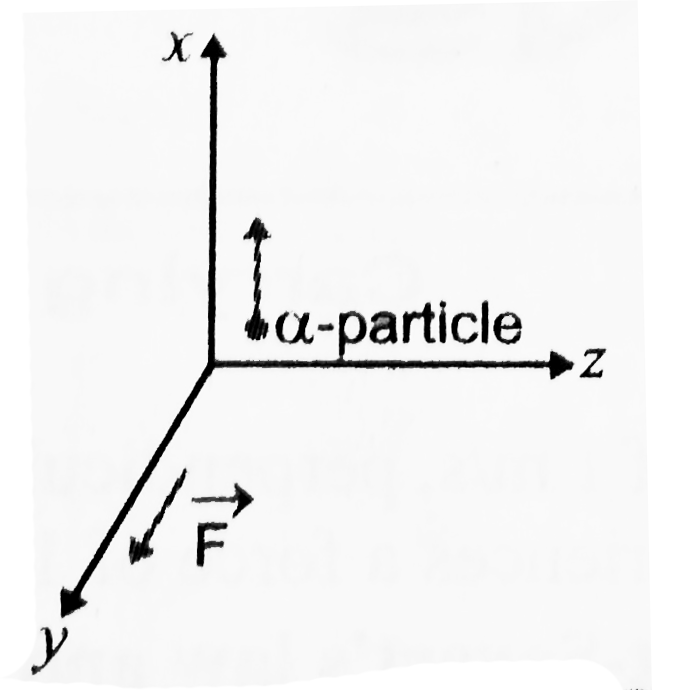
View SolutionIn figure two positive charges q2 and q3 fixed along the y-axis, exert a net electric force in the +x direction on a charge q1 fixed along the x-axis if a positive charge Q is added at (x,0) the force on q1
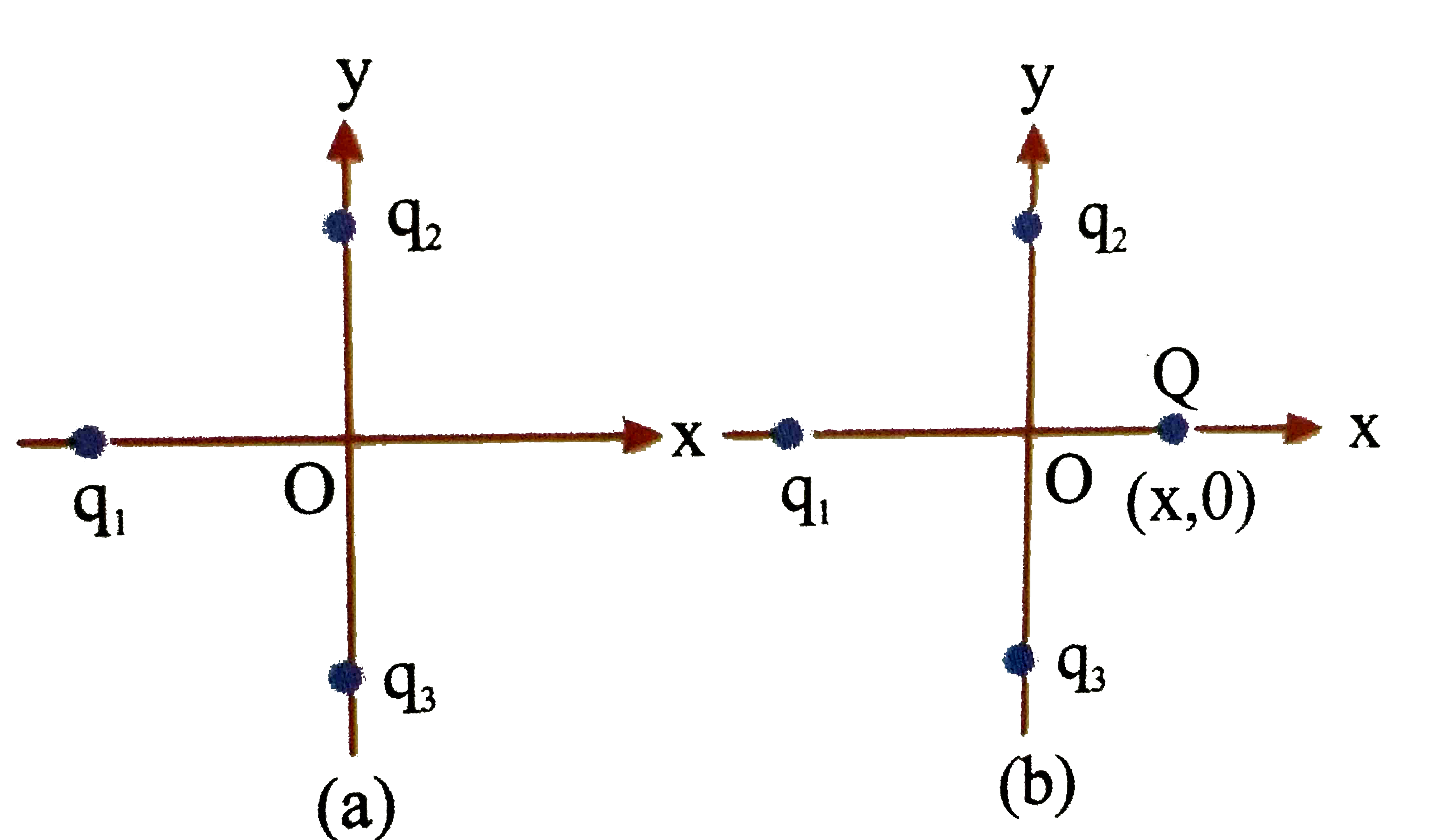
View SolutionIn figure two positive charges q2 and q3 fixed along the y-axis ,exert a net electric force in the +x direction on a charge q1 fixed along the x-axis if a positive charge Q is added at (x,0) the force on q1

View SolutionIn figure two positive charges q2 and q3 fixed along the y-axis ,exert a net electric force in the +x direction on a charge q1 fixed along the x-axis if a positive charge Q is added at (x,0) the force on q1

View SolutionAn electron is projected along positive z-axis, magnetic field is present along y-axis then direction of initial acceleration of the particle is
View Solution
