Angular velocity of smooth parabolic wire y = 4c(x)^(2) about axis of parabola in vertical plane if bead of mass m does not slip at (a,b) will be 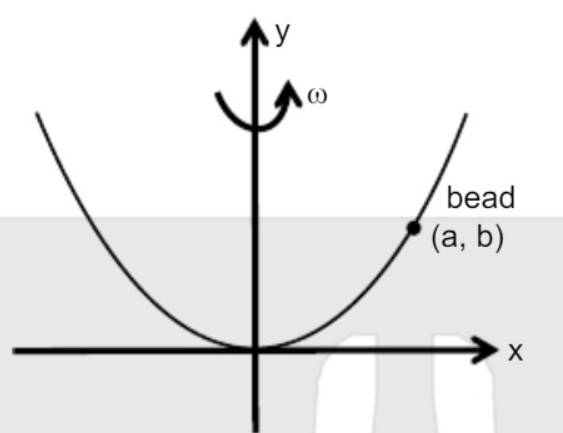
(2gc)^1/2
2((2gc/b)^1/2)
2((2gc/ab)^1/2)
2((2gc)^1/2)
The correct Answer is:D
Step by step video & image solution for Angular velocity of smooth parabolic wire y = 4c(x)^(2) about axis of parabola in vertical plane if bead of mass m does not slip at (a,b) will be by Physics experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Topper's Solved these Questions
Similar Questions
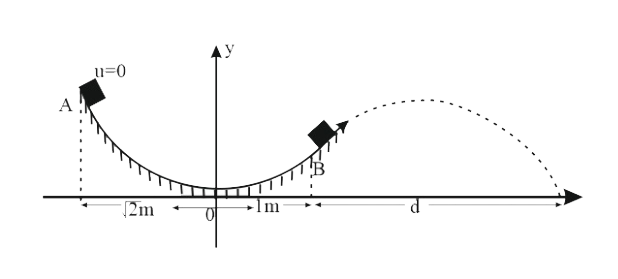
A small body is released from point A of smooth parabolic path y=x2, where y is vertical axis and x is horizontal axis at ground, as shown. The body leaves the surface from point B. If g=10ms−2 then what is the value of d (in m)?
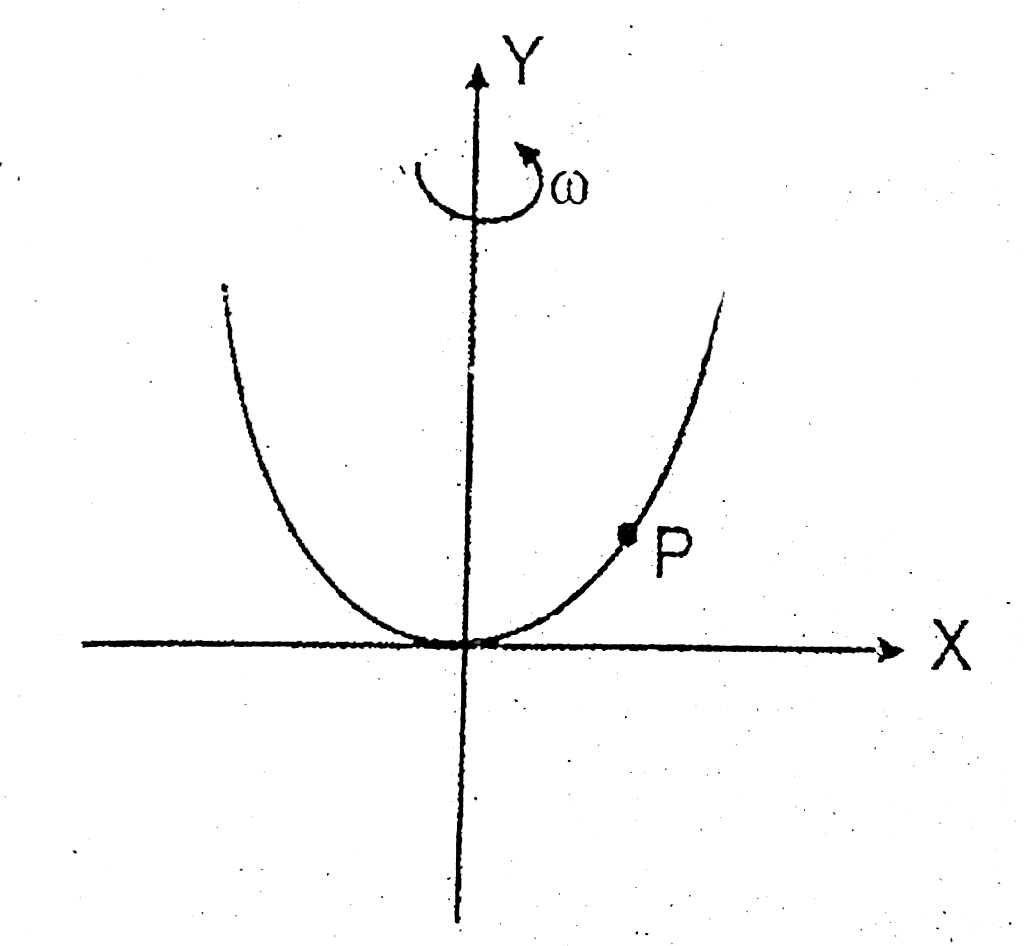
View SolutionA smooth wire frasme is in the shape of a parabola y=5x2 . It is being rotated about y-axis with an angular velocity ω. A small bead of mass (m=1kg) is at point P and is in equilibrium with respect to the frame. Then the angular velocity ω is (g=10m/s2)
View Solution
Knowledge Check
A piece of wire is bent in the shape of a parabola y=kx2 (y-axis vertical) with a bead of mass m on it. The bead can slide on the wire without friction. It stays at the lowest point of the parabola when the wire is at rest. The wire is now accelerated parallel to the x-axis with a constant acceleration a. The distance of the new equilibrium position of the bead, where the bead can stay at rest with respect to the wire, from the y-axis is:
Aa/gkBa/2gkC2a/gkDa/4gk
A piece of wire is bent in the shape of a parabola y=kx2 (y-axis vertical) with a bead of mass m on it. The bead can slide on the wire without friction. It stays at the lowest point of the parabola when the wire is at rest. The wire is now accelerated parallel to the x-axis with a constant acceleration a. The distance of the new equilibrium position of the bead, where the bead can stay at rest with respect to the wire, from the y-axis is:
View SolutionA piece of wire is bent in the shape of a parabola y=kx2 (y-axis vertical) with a bead of mass m on it. The bead can slide on the wire without friction. It stays at the lowest point of the parabola when the wire is at rest. The wire is now accelerated parallel to the x-axis with a constant acceleration a. The distance of the new equilibrium position of the bead, where the bead can stay at rest with respect to the wire, from the y-axis is:
View SolutionA piece of wire is bent in the shape of a parabola y=kx2 (y axis vertical) with a bead of mass mon it. The bead can slide on the wire without friction. It stays at the lowest point of the parabola when the wire is at rest. The wire is now accelerated paralle to the x-axis with a constant acceleration a. The distance of the the new equilibrium position of the bead. Find the x-coordinate where the bead can stay at rest with respect to the wire ?
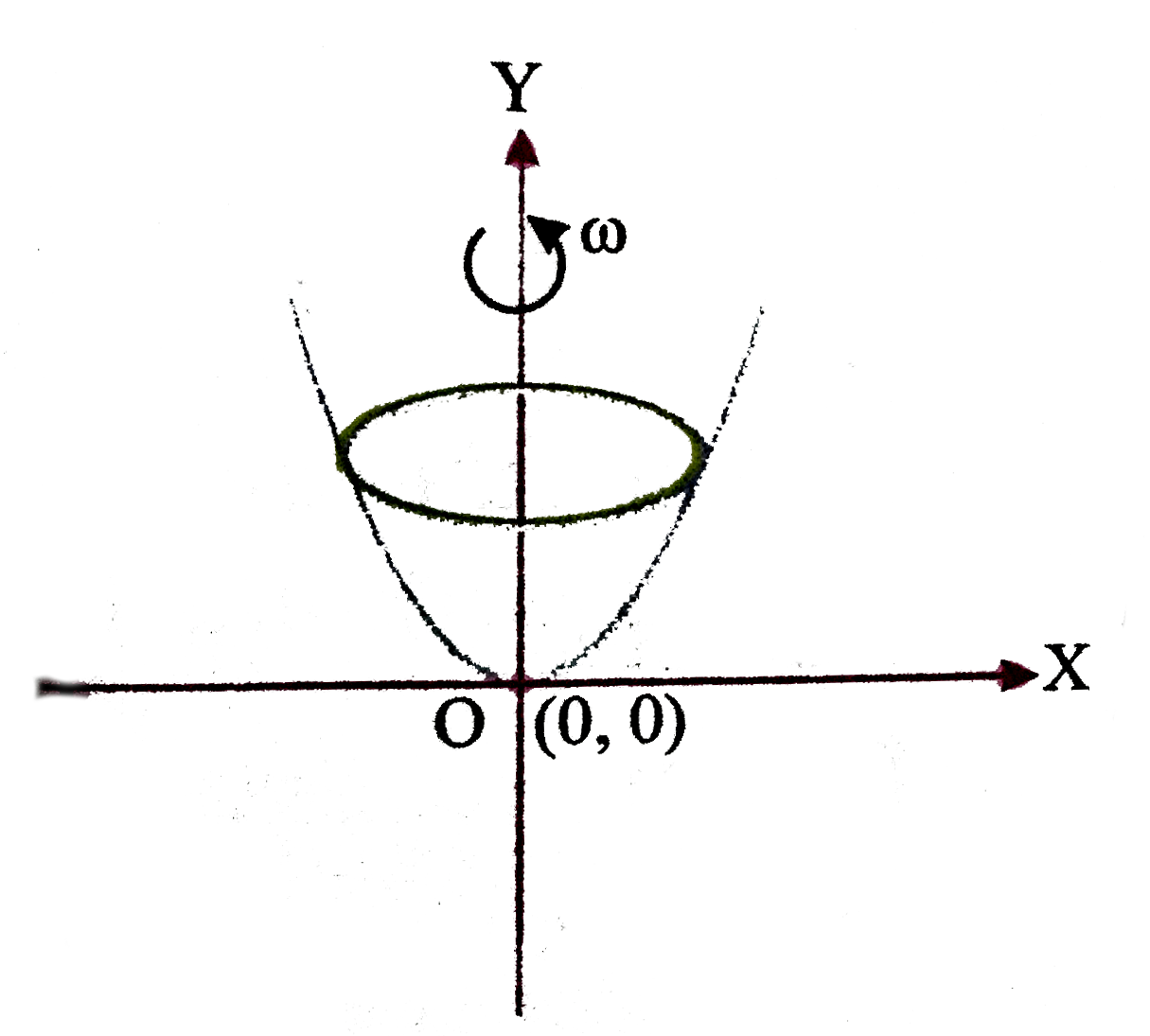
View SolutionIn the given figure, a smooth parabolic wire track lies in the xy-plane (vertical). The shape of track is defined by the equation y=x2. A ring of mass m which can slide freely on the wire track, is placed at the position A(1,1). The track is rotated with constant angular speed ω such that there is no relative slipping between the ring and the track. The value of ω is
View SolutionA particle is placed at the lowest point of a smooth wire frame in the shape of a parabola, lying in the vertical xy-plane having equatioin x2=5y(x,y are in meter). After slight displacement, the particle is set free. Find angular frequency of osciallation (in rad/sec) (Take g=10 m/s2)
View SolutionA bead of mass m is located on a parabolic wire with its axis vertical and vertex at the origin as shown in figure and whose equastion is x2=4ay. The wire frame is fixed and the bead is released from the point y=4a on the wire frame from rest. The tangential acceleration of the bead when it reaches the position given by y=a is

View SolutionA bead of mass m is located on a parabolic wire with its axis vertical and vertex at the origin as shown in figure and whose equastion is x2=4ay. The wire frame is fixed and the bead is released from the point y=4a on the wire frame from rest. The tangential acceleration of the bead when it reaches the position given by y=a is

View Solution
