C1=5.6μF is charged upto 220V. Another capacitor C2=2.8μF is connected in parallel. Find loss in energy ?
To solve the problem, we need to find the loss in energy when a charged capacitor C1 is connected in parallel with another capacitor C2.
1. Calculate the Initial Energy Stored in Capacitor C1:
The initial energy stored in a capacitor is given by the formula:
Ui=12CV2
Where C is the capacitance and V is the voltage. For C1:
- C1=5.6μF=5.6×10−6F
- V=220V
Plugging in the values:
Ui=12×5.6×10−6×(220)2
Ui=12×5.6×10−6×48400
Ui=12×0.270784J
Ui=0.135392J≈0.1354J
2. Calculate the Final Voltage V0 After Connecting C2:
When C2 is connected in parallel, the total capacitance Ctotal is:
Ctotal=C1+C2=5.6μF+2.8μF=8.4μF=8.4×10−6F
The charge Q on C1 before connecting C2 is:
Q=C1×V=5.6×10−6×220
Q=1.232×10−3C
After connecting C2, the voltage across both capacitors will be:
V0=QCtotal=1.232×10−38.4×10−6
V0≈146.67V
3. Calculate the Final Energy Stored in the Combined Capacitors:
The final energy stored in the combined capacitors is:
Uf=12CtotalV20
Uf=12×8.4×10−6×(146.67)2
Uf=12×8.4×10−6×21556.89
Uf=12×0.181J
Uf≈0.0905J
4. Calculate the Loss in Energy:
The loss in energy when C2 is connected is given by:
Loss=Ui−Uf
Loss=0.1354J−0.0905J
Loss≈0.0449J
Final Answer:
The loss in energy is approximately 0.0449J.
The initial energy stored in a capacitor is given by the formula:
Ui=12CV2
Where C is the capacitance and V is the voltage. For C1:
- C1=5.6μF=5.6×10−6F
- V=220V
Ui=12×5.6×10−6×(220)2
Ui=12×5.6×10−6×48400
Ui=12×0.270784J
Ui=0.135392J≈0.1354J
When C2 is connected in parallel, the total capacitance Ctotal is:
Ctotal=C1+C2=5.6μF+2.8μF=8.4μF=8.4×10−6F
The charge Q on C1 before connecting C2 is:
Q=C1×V=5.6×10−6×220
Q=1.232×10−3C
V0=QCtotal=1.232×10−38.4×10−6
V0≈146.67V
The final energy stored in the combined capacitors is:
Uf=12CtotalV20
Uf=12×8.4×10−6×(146.67)2
Uf=12×8.4×10−6×21556.89
Uf=12×0.181J
Uf≈0.0905J
The loss in energy when C2 is connected is given by:
Loss=Ui−Uf
Loss=0.1354J−0.0905J
Loss≈0.0449J
The loss in energy is approximately 0.0449J.
Topper's Solved these Questions
Similar Questions
A 2μF capacitor C1 is charge to a voltage 100 V and a 4μF capacitor C2 is charged to a voltage 50 V. The capacitors are then connected in parallel What is the loss of energy due to parallel connection?
View SolutionA capacitor of capacitor 5.00μF is charged to24.0V and another capacitor of capacitance 6.0μF is charged to 12.0V (a) Find the energy stored in each capacitor .(b)The positive plates of the first capacitor is now connected to the negative plate of the second and vice versa . Find the new charges on the capacitors .(c)Find the loss of electrostatic energy during the process .(d)Where does this energy go?
View Solution
Knowledge Check
Two capacitrors of 2μFand4μF are connected in parallel. A third capacitor of 6μF is connected in series. The combaination is connected across a 12 V battery. The voltage across 2μF capacitor is
A2 VB8 VC6 VD1 V
A capacitor of capacitance 5μF is charged to potential 20V and isolated. Now, an uncharged capacitor is connected in parallel to it. If the charge distributes equally on these capacitors, find total energy stored in capacitors.
View SolutionA capacitor of capacity 2μF is charged to 100V. What is the heat generated when this capacitor is connected in parallel to an another capacitor of same capacity?
View SolutionA 8uF capacitor C1 is charged to V0=120V. The charging battery is then removed and the capacitor is connected in parallel to an uncharged +4μF capacitor C2.
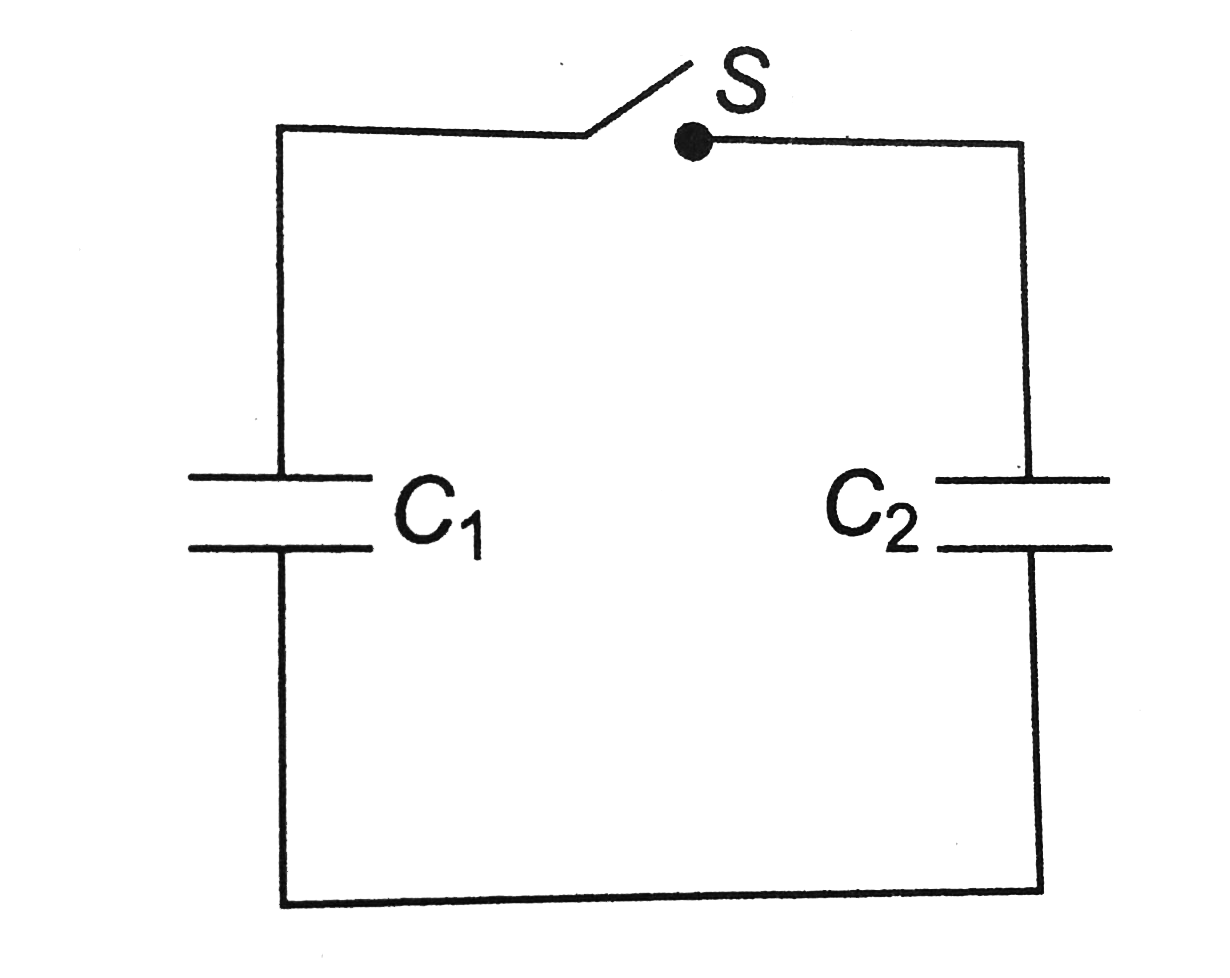
(a) what is the potential difference V across the combination?
(b) what is the stored energy before and after the switch S is closed?
View SolutionA capacitor of capacitance C1=1.0μF charged upto a voltage V=110V is connected in parallel to the terminals of a circuit consisting of two uncharged capacitors connected in series and possessing the capacitance C2=2.0μF and C3=3.0μF. What charge will flow through the connecting wires?
View SolutionFind the charges on 6μF and 4μF capacitors
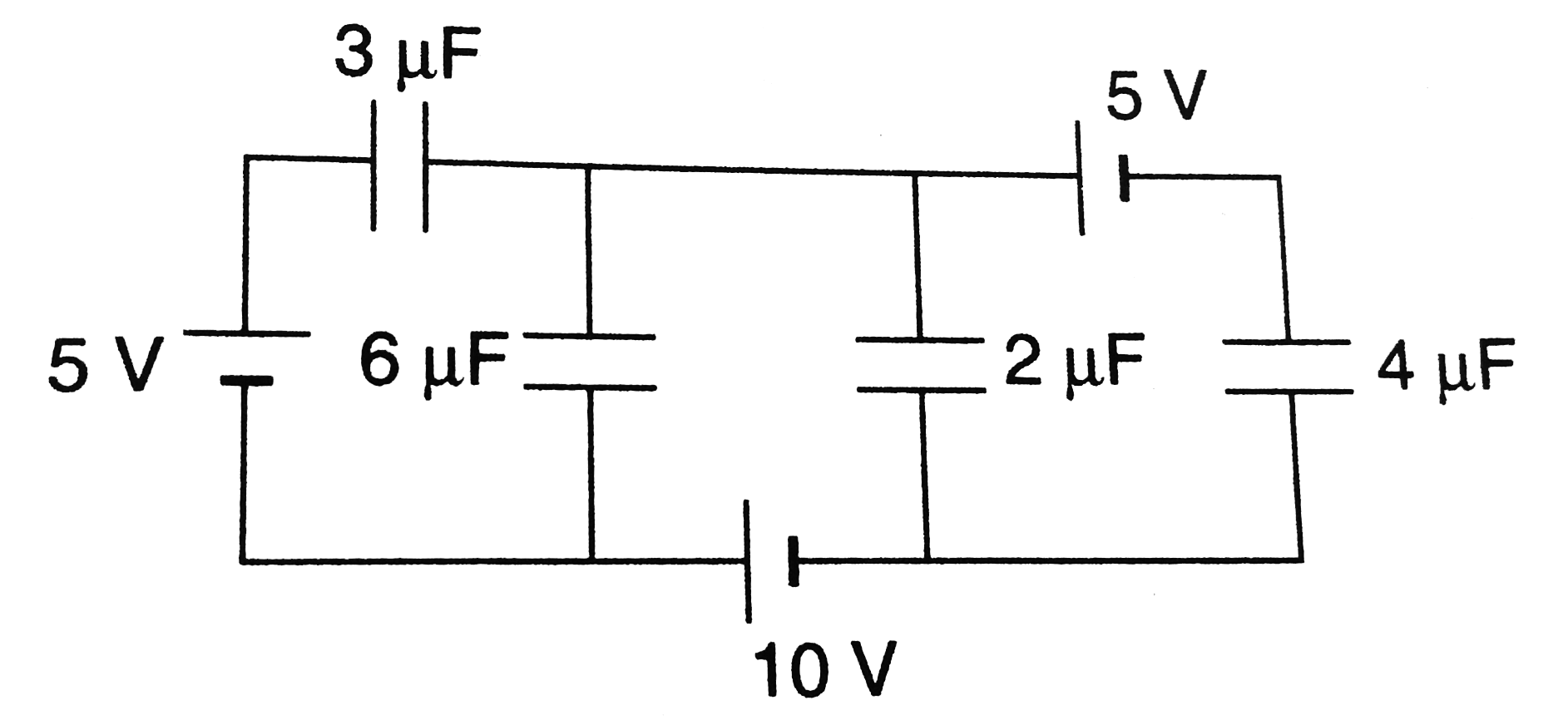
View SolutionA capacitor of capacitance 4μF is charged to 80V and another capacitor of capacitance 6μF is charged to 30V are connected to each other using zero resistance wires such that the positive plate of one capacitor is connected to the positive plate of the other. The energy lost by the 4μF capacitor in the process in X∗10−4J. Find the value of X.
View SolutionA capacitor of capacitance 4μF is charged to 80V and another capacitor of capacitance 6μF is charged to 30V are connected to each other using zero resistance wires such that the positive plate of one capacitor is connected to the positive plate of the other. The energy lost by the 4μF capacitor in the process in X∗10−4J. Find the value of X.
View Solution
