An equiconcave lens has power P. Find power of plano concave lens when given lens is cut in such a way that two plano concave lens are formed.
P
P2
2P
P4
The correct Answer is:B
To solve the problem, we need to determine the power of a plano-concave lens formed by cutting an equiconcave lens with power P into two equal parts. Let's break this down step-by-step.
Step 1: Understanding the Equiconcave Lens
An equiconcave lens is a lens that has two identical concave surfaces. The power P of the lens is related to its focal length F by the formula:
P=1F
Step 2: Lens Maker's Formula for Equiconcave Lens
For an equiconcave lens, the lens maker's formula can be expressed as:
P=(n−1)(1R1−1R2)
where n is the refractive index of the lens material, R1 is the radius of curvature of the first surface (negative for concave), and R2 is the radius of curvature of the second surface (also negative for concave).
For an equiconcave lens with radius of curvature r:
P=(n−1)(−1r−−1r)=(n−1)(−2r)
Thus,
P=−2(n−1)r
Step 3: Cutting the Lens
When the equiconcave lens is cut into two plano-concave lenses, each plano-concave lens will have one flat surface and one concave surface. The power of a plano-concave lens can be calculated using the modified lens maker's formula:
P′=(n−1)(1R1−1R2)
In this case:
- R1=−r (the concave surface)
- R2=∞ (the flat surface)
Thus, the power of one plano-concave lens becomes:
P′=(n−1)(1−r−0)=−(n−1)r
Step 4: Relating the Powers
From the earlier equation for the equiconcave lens, we have:
P=−2(n−1)r
Now, we can express P′ in terms of P:
P′=−(n−1)r=12(−2(n−1)r)=P2
Final Result
Thus, the power of each plano-concave lens formed from the equiconcave lens is:
P′=P2
Conclusion
The power of each plano-concave lens formed by cutting the equiconcave lens is P2.
---
An equiconcave lens is a lens that has two identical concave surfaces. The power P of the lens is related to its focal length F by the formula:
P=1F
For an equiconcave lens, the lens maker's formula can be expressed as:
P=(n−1)(1R1−1R2)
where n is the refractive index of the lens material, R1 is the radius of curvature of the first surface (negative for concave), and R2 is the radius of curvature of the second surface (also negative for concave).
P=(n−1)(−1r−−1r)=(n−1)(−2r)
Thus,
P=−2(n−1)r
When the equiconcave lens is cut into two plano-concave lenses, each plano-concave lens will have one flat surface and one concave surface. The power of a plano-concave lens can be calculated using the modified lens maker's formula:
P′=(n−1)(1R1−1R2)
In this case:
- R1=−r (the concave surface)
- R2=∞ (the flat surface)
P′=(n−1)(1−r−0)=−(n−1)r
From the earlier equation for the equiconcave lens, we have:
P=−2(n−1)r
Now, we can express P′ in terms of P:
P′=−(n−1)r=12(−2(n−1)r)=P2
Thus, the power of each plano-concave lens formed from the equiconcave lens is:
P′=P2
The power of each plano-concave lens formed by cutting the equiconcave lens is P2.
Topper's Solved these Questions
Similar Questions
Find the power of a concave lens of focal length 2m.
View SolutionConcave lens is employed to correct
View SolutionAssertion:A convex lens and a concave lens are kept in contact. They will behave as a diverging lens if focal length of convex lens is more.
Reason: Power of a concave lens is always less than the power of a convex lens, as power of concave lens is negative whereas power of convex lens is positive.
View SolutionWhat is the optical power in dioptre of a concave lens of focal length 50 cm?
View SolutionA double convex lens has power P and same radii of curvature R of both the surfaces. The radius of carvature of a surface of plano-convex lens made of the same meterial with power 1.5 P is :
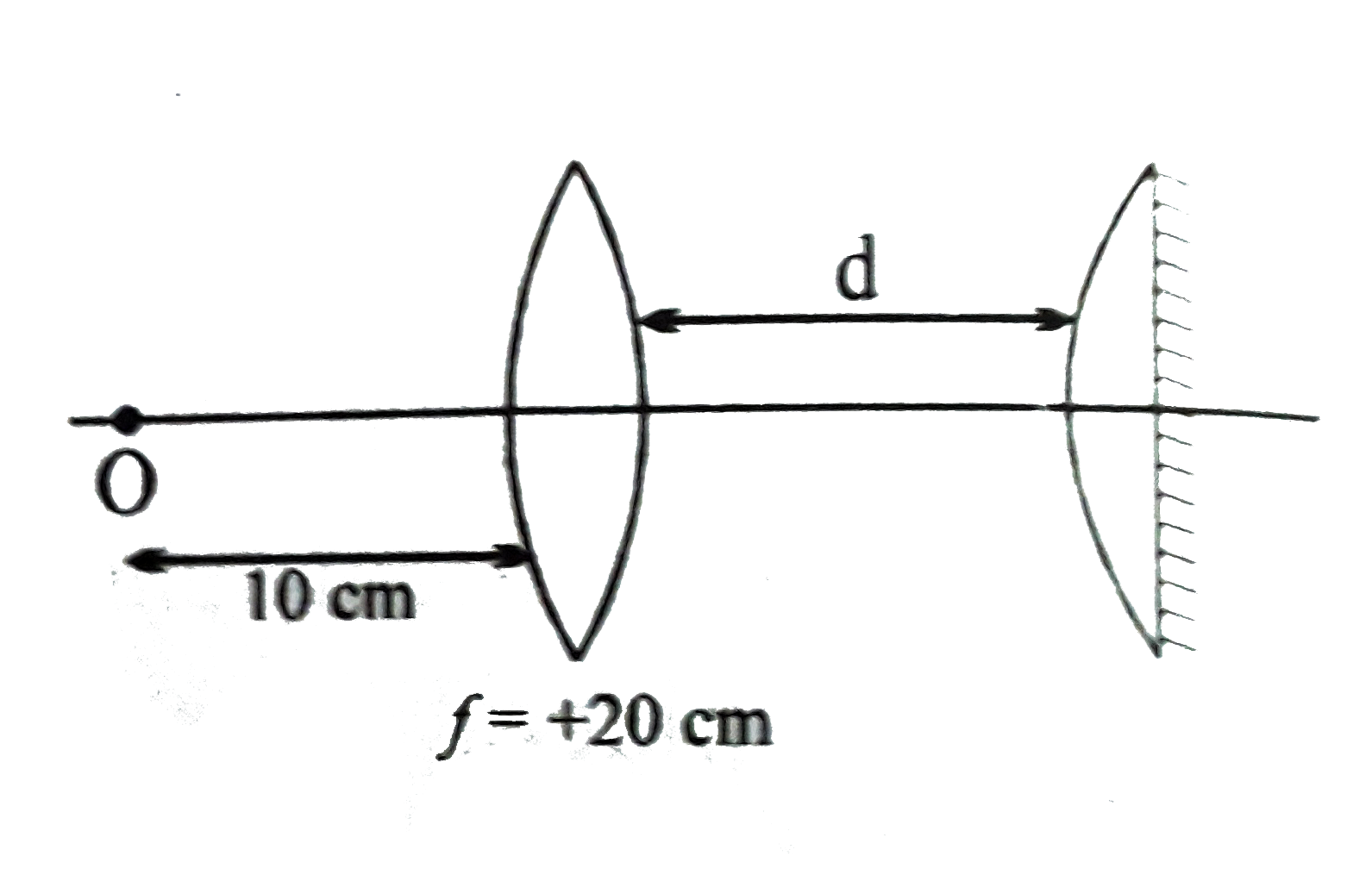
View SolutionA convex lens of focal length 20cm and another plano convex lens of focal length 40cm are placed co-axially . The plano convex lens is silvered on plane surface. What should be the distance (in cm) so that final image of the object 'O' is formed on O itself.
View SolutionDefine the power of a lens.
View SolutionA plano convex lens fits exactly into a plano concave lens. Their plane surfaces are parallel to each other. If the lenses are made of different materials refractive indices μ1 and μ2 and R is the radius curvature of the curved surface of the lenses, the focal length of the combination is
View SolutionA plano convex lens fits exactly into a plano concave lens. Their plane surfaces are parallel to each other. If the lenses are made of different materials refractive indices μ1 and μ2 and R is the radius curvature of the curved surface of the lenses, the focal length of the combination is
View SolutionA plano convex lens fits exactly into a plano concave lens. Their plane surfaces are parallel to each other. If lenses are made of different materials of refractive index μ1=4/3 and μ2=6/5 and R = 40 cm is the radius of curvature of the curved surface of the lenses, then the focal length of combination (in meters) is.

View Solution
