A Tennis ball is released from a height h and after freely falling on a wooden floor it rebounds and reaches height h2. The velocity versus height of the ball during its motion may be represented graphically by :
(graph are drawn schematically and on not to scale )

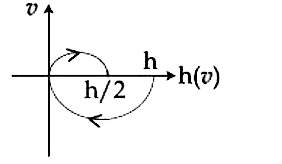
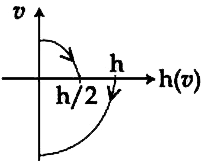
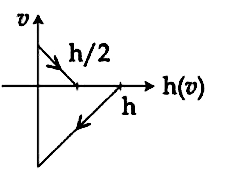
The correct Answer is:B
To solve the problem, we need to analyze the motion of the tennis ball as it falls and rebounds. We will derive the relationship between velocity and height and determine the correct graphical representation.
1. Understanding the Motion:
- The tennis ball is released from a height h.
- It falls freely under the influence of gravity until it hits the ground.
- After hitting the ground, it rebounds to a height of h2.
2. Finding the Velocity Just Before Impact:
- Using the equation of motion:
v2=u2+2gh
where u=0 (initial velocity), g is the acceleration due to gravity, and h is the height.
- Thus, the velocity just before impact (when height is 0) is:
v=√2gh
3. Finding the Velocity Just After Impact:
- After rebounding to a height of h2, we can use the same equation to find the velocity just after the impact when it reaches the height h2:
v′=√2g(h2)=√gh
4. Analyzing the Velocity vs. Height Graph:
- As the ball falls from height h to height 0, its velocity increases from 0 to √2gh.
- After the impact, as the ball rises from height 0 to height h2, its velocity decreases from √2gh to 0.
5. Determining the Nature of the Graph:
- The relationship between velocity and height is not linear. As the ball falls, the velocity increases, and as it rises, the velocity decreases.
- The slope of the velocity vs. height graph will change, indicating a non-linear relationship.
6. Conclusion:
- The correct representation of the velocity vs. height graph will show an increase in velocity as height decreases (falling) and a decrease in velocity as height increases (rising), confirming that the graph is not linear.
- The tennis ball is released from a height h.
- It falls freely under the influence of gravity until it hits the ground.
- After hitting the ground, it rebounds to a height of h2.
- Using the equation of motion:
v2=u2+2gh
where u=0 (initial velocity), g is the acceleration due to gravity, and h is the height.
- Thus, the velocity just before impact (when height is 0) is:
v=√2gh
- After rebounding to a height of h2, we can use the same equation to find the velocity just after the impact when it reaches the height h2:
v′=√2g(h2)=√gh
- As the ball falls from height h to height 0, its velocity increases from 0 to √2gh.
- After the impact, as the ball rises from height 0 to height h2, its velocity decreases from √2gh to 0.
- The relationship between velocity and height is not linear. As the ball falls, the velocity increases, and as it rises, the velocity decreases.
- The slope of the velocity vs. height graph will change, indicating a non-linear relationship.
- The correct representation of the velocity vs. height graph will show an increase in velocity as height decreases (falling) and a decrease in velocity as height increases (rising), confirming that the graph is not linear.
Topper's Solved these Questions
Similar Questions
Knowledge Check
A ball is dropped from a height h on to a floor . If the cofficient of restitution is e, calculate the height the ball first rebounds ?
Ae2hBeh2Ce4hDhe4A ball is dropped from a height h on the ground If the coefficient of restitution is e, the height to which the ball goes up after it rebounds for the nth time is
Ahe2nBhenCe2nhDhe2n
A body falls freely from a height 'h' its average velocity when it reaches earth is
View SolutionA rubber ball falls from a height h and rebounds to a height h/2. A rubber ball of double the mass falling from the same height h rebounds to a height
View SolutionA particle falls from a height h and rebounds to a height h1(h1<h), then which of the graph represents the motion correct ?
View SolutionA ball is released from the top of a tower of height Hm. After 2s is stopped and then instantaneously released. What will be its height after next 2s?.
View SolutionA ball is dropped from a height h on a floor. The coefficient of restitution for the collision between the ball and the floor is e. The total distance covered by the ball before it comes to the rest.
View SolutionA ball is released from the top of a tower of height h metre. It takes T second to reach the ground. What is the position of the ball in T3 second?
View Solution
