A double convex lens has power P and same radii of curvature R of both the surfaces. The radius of carvature of a surface of plano-convex lens made of the same meterial with power 1.5 P is :
2R
R2
3R2
R3
To solve the problem, we need to find the radius of curvature of a surface of a plano-convex lens made of the same material as a double convex lens with given powers. Let's break it down step by step.
Step 1: Understand the relationship between power, focal length, and radius of curvature
The power P of a lens is given by the formula:
P=1f
where f is the focal length of the lens.
Step 2: Use the lens maker's formula
For a lens, the lens maker's formula is:
P=(μ−1)(1R1−1R2)
where μ is the refractive index of the lens material, and R1 and R2 are the radii of curvature of the two surfaces of the lens.
Step 3: Analyze the double convex lens
For the double convex lens with the same radius of curvature R on both surfaces, we have:
P1=(μ−1)(1R−1−R)=(μ−1)(2R)
Thus, we can express this as:
P1=2(μ−1)R
Step 4: Analyze the plano-convex lens
For the plano-convex lens, one surface is flat (infinite radius of curvature) and the other has a radius of curvature R′:
P2=(μ−1)(1R′−1∞)=(μ−1)(1R′)
Thus, we can express this as:
P2=μ−1R′
Step 5: Relate the powers of the lenses
According to the problem, the power of the plano-convex lens is P2=1.5P1:
μ−1R′=1.5⋅2(μ−1)R
This simplifies to:
1R′=3⋅1R
Step 6: Solve for R′
From the above equation, we can find R′:
R′=R3
Conclusion
The radius of curvature of the surface of the plano-convex lens is:
R′=R3
The power P of a lens is given by the formula:
P=1f
where f is the focal length of the lens.
For a lens, the lens maker's formula is:
P=(μ−1)(1R1−1R2)
where μ is the refractive index of the lens material, and R1 and R2 are the radii of curvature of the two surfaces of the lens.
For the double convex lens with the same radius of curvature R on both surfaces, we have:
P1=(μ−1)(1R−1−R)=(μ−1)(2R)
Thus, we can express this as:
P1=2(μ−1)R
For the plano-convex lens, one surface is flat (infinite radius of curvature) and the other has a radius of curvature R′:
P2=(μ−1)(1R′−1∞)=(μ−1)(1R′)
Thus, we can express this as:
P2=μ−1R′
According to the problem, the power of the plano-convex lens is P2=1.5P1:
μ−1R′=1.5⋅2(μ−1)R
This simplifies to:
1R′=3⋅1R
From the above equation, we can find R′:
R′=R3
The radius of curvature of the surface of the plano-convex lens is:
R′=R3
Topper's Solved these Questions
Similar Questions
A double convex lens has focal length 25 cm. The radius of curvature of one of the surfaces is double of the other. Find the radii, if the refractive index of the material of the lens is 1.5.
View SolutionA thin plano-convex lens acts like a concave mirror of radius of curvature 20cm when its plane surface is silvered. The radius of curvature of the curved surface if index of refraction of its matarial is 1.5 will be
View Solution
Knowledge Check
The radius curvature of each surface of a convex lens of refractive index 1.5 is 40 cm. Calculate its power.
A2.5DB2DC1.5DD1DThe radius of curvature of the curved surface of a plano-convex lens is 20cm. If the refractive index of the material of the lens be 1.5, it will
Aact as a convex lens only for the objects that lie on its curved side.Bact as a concave lens for the objects that lie on its curved side.Cact as a convex lens irrespective of the side on which the object lies.Dact as a concave lens irrespective of side on which the object lies.The power of a biconvex lens is 10 dioptre and the radius of curvature of each surface is 10 cm. Then the refractive index of the material of the lens is
A32B43C98D53
A thin plano-convex lens acts like a concave mirror of radius of curvature 20cm when its plane surface is silvered. The radius of curvature of the curved surface if index of refraction of its matarial is 1.5 will be
View SolutionThe radius of curvature of the convex surface of a thin plano-convex lens is 12 cm, and the refractive index of its material is 1.6. What is the power of lens ?
View SolutionFind the focal length of the lens shown in Fig . The radii of curvature of both the surfaces are equal to R.
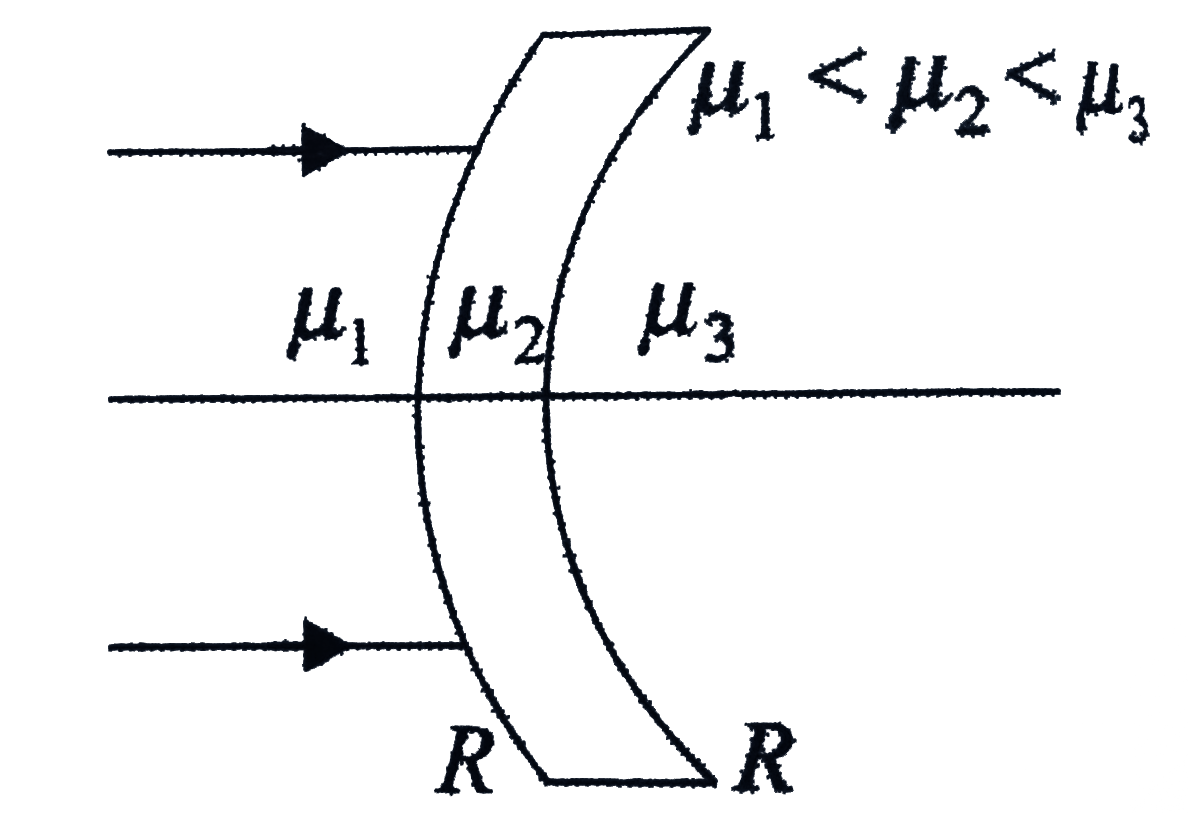
View SolutionThe effective focal length of the lens combination shown in figure is -60 cm. The radius of curvature of the curved surfaces of the plano-convex lenses are 12 cm each and refractive index of the material of the lens is 1.5. The refractive index of the liquid is
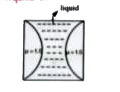
View SolutionThe convex side of a thin concavo-convex lens of glass of refractive index 1.5 has a radius of curvature of 20cm. The concave surface has a radius of curvature of 60cm. What is the focal length of the lens? The convex side is silvered and placed on a horizontal surface. What is the effective focal length of the silvered lens? The concave part is filled with water with refractive index 1.33. What is the effective focal length of the combined glass and water lens? If the convex side is silvered what is the new effective focal length of the silvered compound lens?
View Solution