The linear mass density of a thin rod AB of length L varies from A to B as λ(x)=λ0(1+xL). Where x is the distance from A. If M is the mass of the rod then its moment of inertia about an axis passing through A and perpendicualr to the rod is :
512ML2
718ML2
25ML2
37ML2
To find the moment of inertia of a thin rod AB with a varying linear mass density about an axis passing through point A and perpendicular to the rod, we can follow these steps:
1. Define the Linear Mass Density:
The linear mass density of the rod is given by:
λ(x)=λ0(1+xL)
where x is the distance from point A.
2. Determine the Mass Element:
Consider a small element of the rod of length dx at a distance x from A. The mass dm of this element can be expressed as:
dm=λ(x)dx=λ0(1+xL)dx
3. Calculate the Moment of Inertia of the Element:
The moment of inertia dI of this small mass element about the axis through A is given by:
dI=x2dm=x2⋅λ0(1+xL)dx
4. Integrate to Find the Total Moment of Inertia:
To find the total moment of inertia I of the rod, integrate dI from x=0 to x=L:
I=∫L0dI=∫L0x2⋅λ0(1+xL)dx
Expanding the integrand:
I=λ0∫L0(x2+x3L)dx
This can be separated into two integrals:
I=λ0(∫L0x2dx+1L∫L0x3dx)
5. Evaluate the Integrals:
The integrals can be evaluated as follows:
∫L0x2dx=L33
∫L0x3dx=L44
Substituting these results back into the equation for I:
I=λ0(L33+1L⋅L44)
Simplifying this gives:
I=λ0(L33+L34)=λ0(4L312+3L312)=λ0⋅7L312
6. Find the Total Mass of the Rod:
The total mass M of the rod can be calculated as:
M=∫L0dm=∫L0λ0(1+xL)dx
Evaluating this integral:
M=λ0(∫L01dx+1L∫L0xdx)=λ0(L+1L⋅L22)=λ0(L+L2)=λ0⋅3L2
7. Express λ0 in terms of M:
From the mass equation, we can express λ0:
λ0=2M3L
8. Substitute λ0 back into the Moment of Inertia:
Substitute λ0 into the moment of inertia equation:
I=(2M3L)⋅7L312=14ML236=7ML218
Final Result:
Thus, the moment of inertia of the rod about the axis through A and perpendicular to the rod is:
I=718ML2
The linear mass density of the rod is given by:
λ(x)=λ0(1+xL)
where x is the distance from point A.
Consider a small element of the rod of length dx at a distance x from A. The mass dm of this element can be expressed as:
dm=λ(x)dx=λ0(1+xL)dx
The moment of inertia dI of this small mass element about the axis through A is given by:
dI=x2dm=x2⋅λ0(1+xL)dx
To find the total moment of inertia I of the rod, integrate dI from x=0 to x=L:
I=∫L0dI=∫L0x2⋅λ0(1+xL)dx
Expanding the integrand:
I=λ0∫L0(x2+x3L)dx
This can be separated into two integrals:
I=λ0(∫L0x2dx+1L∫L0x3dx)
The integrals can be evaluated as follows:
∫L0x2dx=L33
∫L0x3dx=L44
Substituting these results back into the equation for I:
I=λ0(L33+1L⋅L44)
Simplifying this gives:
I=λ0(L33+L34)=λ0(4L312+3L312)=λ0⋅7L312
The total mass M of the rod can be calculated as:
M=∫L0dm=∫L0λ0(1+xL)dx
Evaluating this integral:
M=λ0(∫L01dx+1L∫L0xdx)=λ0(L+1L⋅L22)=λ0(L+L2)=λ0⋅3L2
From the mass equation, we can express λ0:
λ0=2M3L
Substitute λ0 into the moment of inertia equation:
I=(2M3L)⋅7L312=14ML236=7ML218
Thus, the moment of inertia of the rod about the axis through A and perpendicular to the rod is:
I=718ML2
Topper's Solved these Questions
Similar Questions
The linear density of a thin rod of length 1m lies as λ=(1+2x), where x is the distance from its one end. Find the distance of its center of mass from this end.
View SolutionThe liner density of a rod of length 2m varies as λ=(2+3x) kg/m, where x is distance from end A . The distance of a center of mass from the end B will be
_PHY_E05_180_Q02.png)
View SolutionMoment of inertia of a thin rod of mass m and length l about an axis passing through a point l/4 from one end and perpendicular to the rod is
View SolutionLinear mss density (mass/length) of a rod depends on the distanec from one end (say A) as λx=(αx+β) here α and β are constants, find the moment of inertia of this rod about an axis passing through A and perpendicular to the rod. Length of the rod is l.
View SolutionA particle mass m is attched to a thin uniform rod of length a at a distance of a4 from the mid-point C as shown in the figure. The mass of the rod is 4m
The moment of inertia of the combined system about an axis passing through O and perpendicular to the rod is
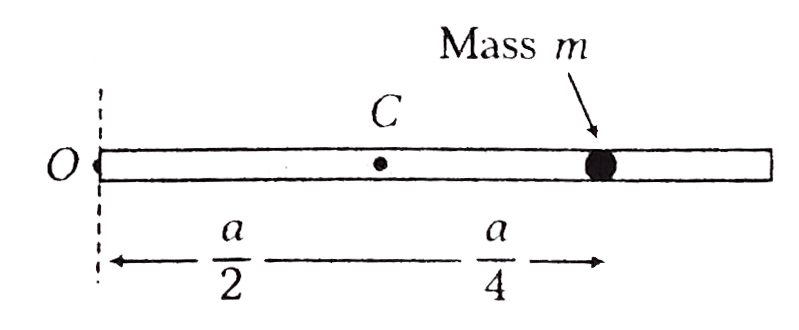
View Solution
Linear mass density of the two rods system, AC and CD is x. moment of inertia of two rods about an axis passing through AB is
View SolutionA uniform rod of mass m is bent into the form of a semicircle of radius R. The moment of inertia of the rod about an axis passing through A and perpendicular to the plane of the paper is

View SolutionA uniform rod of mass m is bent into the form of a semicircle of radius R. The moment of inertia of the rod about an axis passing through A and perpendicular to the plane of the paper is

View SolutionLinear mass density of a rod AB(of≤n>h10m) varies with distance x from its end A as λ =λ0x3 (λ0 is positive constant) . Distance of centre of mass of the rod , from end B is
View SolutionLinear mass density of a rod AB ( of length 10 m) varied with distance x from its end A as λ=λ0x3 (λ0 is poitive constant). Distance of centre of mass the rod, form end B is
View Solution
