Question

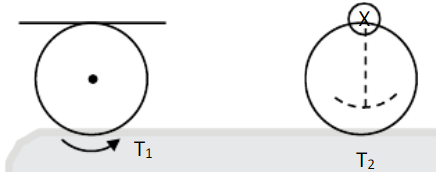
A ring is hung on a nail. It can oscillate without slipping or sliding (i) in its plane with a time period $T_1$ and (ii) , back and forth in a direction perpendicular to its plane , with a period $T_2$. The ratio $\frac{T_1}{T_2}$ will be :

Options

A. `(2)/(sqrt(3))`
B. `(2)/(3)`
C. `(3)/(sqrt(3))`
D. `(sqrt(2))/(3)`

Explanation

To solve the problem, we need to find the ratio of the time periods $$T_1$$ and $$T_2$$ for a ring oscillating in two different modes.

1. Understanding the Problem:
- The ring can oscillate in its plane (time period \( T_1 \)) and back and forth in a direction perpendicular to its plane (time period \( T_2 \)).
- We need to find the ratio \( \frac{T_1}{T_2} \).

2. Time Period of Oscillation in Plane (T1):
- For a ring oscillating in its plane, we can derive the equation of motion using the moment of inertia about the point of suspension.
- The moment of inertia \( I_1 \) about the nail is given by:
\( I_1 = 2MR^2 \)
where \( M \) is the mass of the ring and \( R \) is its radius.
- The angular frequency \( \omega_1 \) for small oscillations can be expressed as:
\( \omega_1 = \sqrt{\frac{g}{L}} \)
- Therefore, the time period \( T_1 \) is:
\( T_1 = 2\pi \sqrt{\frac{I_1}{k}} = 2\pi \sqrt{\frac{2MR^2}{Mg}} = 2\pi \sqrt{\frac{2R^2}{g}} \)

3. Time Period of Oscillation Perpendicular to the Plane (T2):
- For oscillation in a direction perpendicular to its plane, the moment of inertia \( I_2 \) is given by:
\( I_2 = \frac{1}{2}MR^2 + MR^2 = \frac{3}{2}MR^2 \)
- The angular frequency \( \omega_2 \) for this motion can be expressed as:
\( \omega_2 = \sqrt{\frac{g}{L}} \)
- Therefore, the time period \( T_2 \) is:
\( T_2 = 2\pi \sqrt{\frac{I_2}{k}} = 2\pi \sqrt{\frac{\frac{3}{2}MR^2}{Mg}} = 2\pi \sqrt{\frac{3R^2}{2g}} \)

4. Finding the Ratio \( \frac{T_1}{T_2} \):
- Now we can find the ratio of the two time periods:
\( \frac{T_1}{T_2} = \frac{2\pi \sqrt{\frac{2R^2}{g}}}{2\pi \sqrt{\frac{3R^2}{2g}}} \)
- Simplifying this gives:
\( \frac{T_1}{T_2} = \frac{\sqrt{2}}{\sqrt{\frac{3}{2}}} = \frac{\sqrt{2}}{\sqrt{3}/\sqrt{2}} = \frac{2}{\sqrt{3}} \)

5. Final Answer:
- Thus, the ratio \( \frac{T_1}{T_2} \) is:
\( \frac{T_1}{T_2} = \frac{2}{\sqrt{3}} \)